Основні поняття

Предмет дисципліни

Предметом вивчення дисципліни ТОЕ є електромагнітні явища і їх використання для генерування, передачі і розподілу електроенергії, вирішення проблем електромеханіки, електротехнології, електроенергетики і т.п.

Мета і завдання кредитного модуля

Метою даного кредитного модуля є вивчення основних законів теорії електричних кіл постійного та синусоїдного струму, ознайомлення з математичними методами їх аналізу та моделювання.

Вивчення кредитного модуля дає такі знання:

1) методів аналізу усталених процесів в лінійних електричних колах постійного та однофазного синусоїдного струму;

2) енергетичних процесів в електричних колах.

Вміння:

1) формування математичної моделі кола;

2) розрахувати усталений режим в лінійному електричному колі, в якому діють джерела постійної та синусоїдної ЕРС;

3) скласти рівняння електричного балансу електричного кола.

Навички:

1) практичного застосування методів моделювання і розрахунку процесів у технічних пристроях , принцип дії яких оснований на використанні електромагнітних явищ;

2) проведення електричних досліджень і узагальнення їх результатів;

3) використання електровимірювальної апаратури;

4) самостійної роботи з навчальною та методично-навчальною літературою.

ЛІНІЙНІ ЕЛЕКТРИЧНІ КОЛА ПОСТІЙНОГО СТРУМУ

Основні поняття

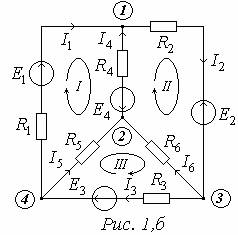
Електричне коло – це сукупність пристроїв для проходження електричного струму. Цей шлях завжди є замкненим. В електричному колі відбувається розподіл, перетворення та передача електричної енергії. Складові кола, що виконують певні функції, називатимемо його елементами.

Електрична схема –зображення електричного кола за допомогою умовних знаків.

Елементи схеми:

1. Вузол – точка в якій сходяться не менше трьох струмів (точка розгалуження струмів). Маємо чотири вузли: 1,2,3,4.

2. Вітка – частина кола між двома суміжними вузлами, по вітці протікає один струм. Маємо шість віток.

3. Контур – будь-який замкнений шлях, що проходить по кількох вітках.

4. Незалежний контур – відрізняється від інших (раніше обраних) хоч би однією віткою. У якості одного із можливих варіантів маємо три незалежних контури, які позначені римськими цифрами.

Класифікація елементів електричного кола

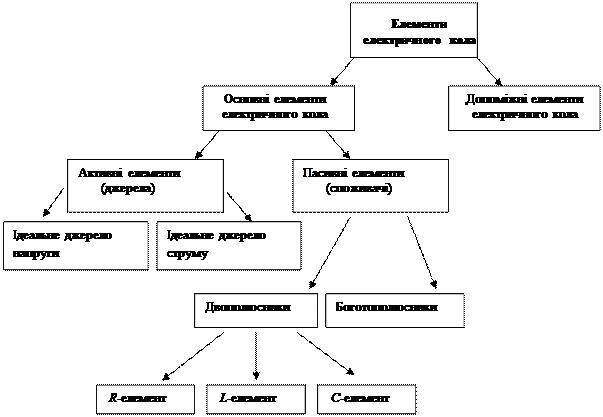
До основних елементів відносяться ті, дія яких пов’язана з перетворенням одного виду енергії на інший. Виходячи з цього, основними елементами електричного кола є джерела електричної енергії та її споживачі. Усі інші елементи – допоміжні(з’єднувальні проводи, вимірювальна апаратура тощо).

Всі елементи електричного кола умовно можна розділити на активні й пасивні. Активним називається елемент, що містить у своїй структурі джерело електричної енергії. До пасивного відносяться елементи, у яких енергія розсіюється (резистори) або накопичується (котушка індуктивності й конденсатори).

У кожного елемента кола можна виділити певне число затискачів (полюсів), за допомогою яких він з'єднується з іншими елементами. Розрізняють дво- та багатополюсні елементи. Двополюсники мають два затискачі. До них відносяться джерела енергії (за винятком керованих та багатофазних), резистори, котушки індуктивності, конденсатори. Прикладом багатополюсних елементів є тріоди, трансформатори, підсилювачі й т.д.

До основних характеристик елементів кола відносяться їх вольт-амперні, вебер-амперні й кулон-вольтні характеристики, які описуються диференціальними або (і) алгебраїчними рівняннями. Якщо елементи описуються лінійними диференціальними або алгебраїчними рівняннями, то вони називаються лінійними, у противному випадку вони відносятьсядо класу нелінійних. Слід зазначити, що у реальних колах всі елементи є нелінійними. Розгляд їх як лінійних, надає можливість істотно спростити математичний опис й аналіз процесів, який визначається межами зміни характеризуючих їх змінних й їхніх частот. Коефіцієнти, що зв'язують змінні, їхні похідні й інтеграли в цих рівняннях, називаються параметрами елемента.

Якщо параметр елемента не є функцією просторових координат, що визначає його геометричні розміри, то він називаєтьсяелементом із зосередженими параметрами. Якщо елемент описується рівняннями, у які входять просторові змінні, то він відноситься до класу елементів з розподіленими параметрами. Класичним прикладом останніх є лінія передачі електроенергії (довга лінія).

Кола, що містять тільки лінійні елементи, називаються лінійними. Наявність у схемі хоча б одного нелінійного елемента відносить її до класу нелінійних.

В реальних схемах елементи між собою з’єднуються між собою за допомогою проводів, металевих провідників, кожний з яких в кожній точці має одну й ту ж саму напругу (наприклад, по відношенню до землі). В області високих частот або низьких повних опорів таке твердження не зовсім справедливе. Але для спрощення розрахунків прийнято таке припущення.

Усіх споживачів вважають пасивними. Елементи електричного кола, які не є джерелами чи споживачами – це вимірювальна і комутаційна апаратура, з’єднувальні проводи і т.п.

1.2. Основні елементи електричного кола

ПАСИВНІ

Двополюсні пасивні елементи електричних кіл:

реальні й ідеалізовані елементи схем заміщення кіл

Споживач електричної енергії – це пристрій, у якому електрична енергія перетворюється на будь-яку іншу. Як приклад: електричний двигун, лампочка розжарювання, електронагрівач тощо.

Незважаючи на велику різноманітність споживачів електричної енергії, які використовують на практиці, задачу аналізу процесів у них спрощують і уніфікують шляхом моделювання елементів (ком­понентів) електричного кола. Побудова моделей пасивних елементів чи, інакше, схем заміщення елементів, які б досить повно враховували зв'язок між струмами і напругами на їх затискачах, є такою ж складною за­дачею, як і для активних елементів. Для її розв'язання потрібно, у першу чергу, знати фізичні властивості елемента і можливий харак­тер електромагнітного процесу в ньому залежно від характеристики сигналу.

Створюючи оптимальну схему заміщення будь-якого пасивного елемен­та електричного кола, слід спиратися на розуміння, що модель, побудова­на з урахуванням несуттєвих факторів, ускладнює розв'язання задачі, а інколи й унеможливлює його. Тому, моделюючи елементи електричного кола, доцільно обмежуватися такою схемою заміщення, яка відображає найсуттєвіші сторони процесу, що аналізується.

Для аналізу процесів у реальних колах та здійснення розрахунків для кожного кола слід скласти схему заміщення всього кола.

Схема заміщення кола – це схема, яка складена тільки з ідеалізованих пасивних і активних елементів, з’єднаних таким чином, щоб якомога точніше відображати електромагнітні процеси, які мають місце у реальному колі.

Резистори

Резистори – це елементи електричного кола, що характеризуються влас­тивістю необоротно перетворювати електричну енергію на теплову. Кількість енергії, що перетворюється на теплову визначається законом Джоуля-Ленца.

На резистивному елементі зв'язок між струмом та напругою визначається законом Ома:

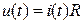, (1.1)

Формула (1.1) дійсна для миттєвих значень напруги та струму.

Коефіцієнт пропорційності R вважають параметром ідеалізованого резистивного елемента, значення якого залежить від геометрії резистора і його матеріалу. Для прямолінійного провідника:

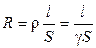, (1.2)

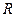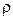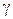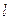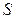де – опір резистора; – питомий опір; – питома провідність; та – довжина та поперечний переріз провідника, відповідно.

В загальному випадку визначення опору пов’язано з розрахунком поля в провідному середовищі, що розділяє два електроди.

Опір 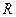– основна характеристика резистивного елемента. Резистор найчастіше подають як електричний опір. За постійного стру­му його називають омічним. Опір того ж резистора, який находиться в колі змінного струму, називають активним. На високих частотах активний опір більший від омічного, що поясню­ється поверхневим ефектом, тобто нерівномірним розподілом струму по перерізу провідника. Для промислових частот активний та омічний опори провідника практично однакові.

У схемах заміщення електричних кіл перетворення енергії на теплоту та її випромінювання моделюють за допомогою ідеалізованих резисторів, таких двополюсних пасивних елементів, в яких відбувається лише перетво­рення електричної енергії на теплоту і не існує електричного та магнітно­го полів. Умовне позначення резистора зображено на рис. 1.1.

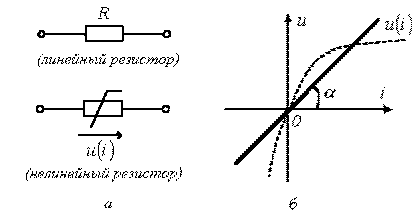
Рис. 1.1. Умовне позначення ідеалізованого резистора

Як зазначалося раніше, струм з напругою на опорі пов'язані за законом Ома (див. формулу (1.1)). Умовні додатні напрямки напруги та струму завжди обирають однаковими, у такому разі їх знаки збігаються і 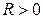. Одиниця вимірювання опору має назву ом (Ом)на честьфізика Георга Ома, який експериментально довів закон (1.1).

Параметр, значення якого є оберненим до величини опору, називається провідністю і вимірюється в сименсах (См): 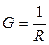. (1.3)

Розглянемо електричне коло, що зображено на рис. 1.2, а) і припустимо, що в ньому діє постійний сигнал 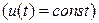. У такому разі струм буде також постійним: 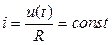(рис. 1.2, б).

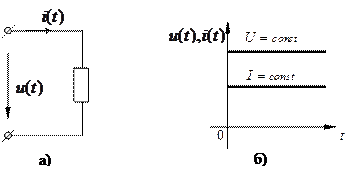
Рис. 1.2. Електричне коло постійного струму (а),

часові графіки вхідного струму і вхідної напруги (б)

Миттєва потужність, яку споживає резистор, у колі з постійним струмом є сталою величиною: .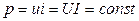

Використовуючи закон Ома, одержимо іншу форму запису формули для обчислення потужності резистора:

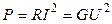. (1.4)

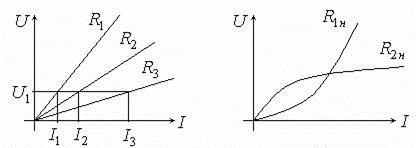
Вольтамперна характеристика – залежність струму, що проходить через елемент від напруги на ньому. ВАХ можуть бути лінійними і нелінійними.

а) б)

Рис. 1.3. ВАХ для лінійних опорів

На рис.1.3,а показані ВАХ для лінійних опорів R₁, R₂, R₃. Оскільки при однаковій напрузі U₁ струми різні (I₁, I₂, I₃) можна зробити висновок, що R₁ >R₂> R₃.

Конденсатори

Джерела електричної енергії зі сторонніми силами здатні роз'єднувати електричні заряди різних знаків, які накопичуються на електродах джерел. Значен­ня накопиченого заряду залежить від ЕРС джерела і геометричних розмірів електро­дів. Якщо до затискачів джерела (рис. 1.4) під'єднати металеві обкладки зі збільшеною поверхнею, то накопичений заряд збільшиться.

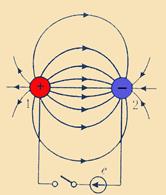
Рис. 1.4 Два електроди, до яких приєднано джерело енергії

Якщо між металевими тілами розташо­ваний ідеальний діелектрик, заряди на них зберігаються і після вимкнення джерела. Таку фізичну властивість металевих тіл використовують в електротехнічних при­строях, які називають конденсаторами. Конденсатори призначені для накопичення електричних зарядів і зосередження електричного поля в певній ділянці простору. Це два металевих тіла (обкладки), які розділені діелектриком.

Для кількісної характеристики зазначених властивостей конденсаторів введено поняття електричної ємності. Електрична ємність – це скалярна фізична величина, яка характеризує властивість конденсатора накопичувати та утримувати електричні заряди і чисельно дорівнює відношенню абсолютного значення заряду на будь-якій з обкладок до напруги між обкладками:

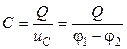. (1.5)

Одиниця ємності – фарада (Ф): .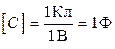

Від чого залежить ємність? Розглянемо плоский конденсатор, площа обкладок якого 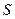і вони розділені діелектриком товщиною 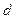(рис. 1.5.). Діелектричну проникність діелектрика позначають .

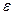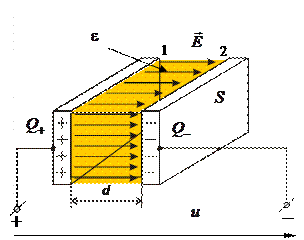
Рис. 1.5. Плоский конденсатор

Припустимо, що між обкладками діє однорідне електричне поле. Таке поле утвориться, якщо між пластинами конденсатора діє постійна напруга і на пластинах накопичені однакові за величиною 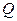і протилежні за знаком заряди. Такі заряди створюють у діелектрику електричне поле з напруженістю 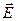, яке, нехтуючи крайовим ефектом, можна вважати однорідним.

Виходячи з теореми Гауса 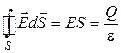, визначимо напруженість електричного поля в діелектрику:

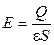. (1.6)

Напруга між обкладками конденсатора, якщо шлях інтегрування проходить вздовж силової лінії 1-2:

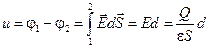
Ємність плоского конденсатора:

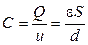(1.7)

Аналіз формули (1.7) веде до висновку, що ємність 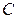залежить від геометричних розмірів конденсатора. Якщо розміри конденсатора незмінні, а діелектрик ізотропний ( 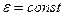), то ємність також постійна за значенням ( 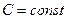); у супротивному випадку 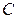– змінна величина.

Формула (1.7) також вказує на можливі способи збільшення ємності конденсаторів:

· використання діелектриків з якнайбільшою діелектричною проникністю діелектрика ;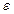

· збільшення площі 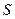обкладок;

· зменшення відстані 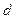між обкладками.

Реальні елементи електричних кіл – конденсатори – з часом втрачають накопичену енергію, тобто мають втрати. На схемах заміщення конденсатори найчастіше подають ємністю і паралельно (або послідов­но) з'єднаним з нею опором. Ідеальний конденсатор – це безвтратний конденсатор, який характеризується тільки ємністю і на розрахункових схемах представлений ідеалізованим ємнісним елементом (рис. 1.6).

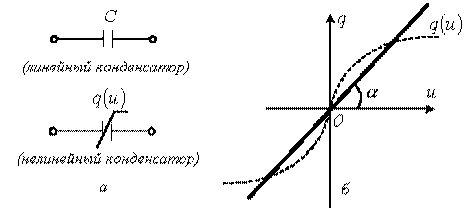
Рис. 1.6. Умовне позначення ідеалізованого ємнісного елемента

Додатні напрямки напруги та струму на ємнісному елементі завжди обирають однаковими, щоб величина ємності була додатною.

Якщо до конденсатора прикласти змінну напругу 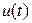, заряди на його обкладинках будуть змінюватися і в колі буде проходити струм 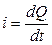. Цей струм (як струм провідності) проходить у провідниках кола, а враховуючи неперервність електричного струму, він повинен існувати і в діелектрику, між обкладинками конденсатора, що можливо лише у разі виникнення між обкладинками струму зміщення :

.

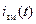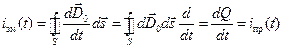Отже, 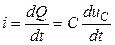. (1.8)

Зауваження. Нагадаємо, що змінні заряди на обкладинках конденсатора утворюють у діелектрику змінне електричне поле, внаслідок чого діелектрик поляризується: відбувається зміщення заряджених частинок, що входять до складу молекул діелектрика, у протилежних напрямках. Молекули перетворюються на диполі, тобто на систему двох протилежних за знаком точкових зарядів. У процесі поляризації має місце рух елементарних частинок у межах молекул. Цей рух утворює струм зміщення, який існує доки існує в діелектрику змінне електричне поле.

Слід пам’ятати, що лінії електричного струму, як і магнітні, завжди замкнені. Лінії струму провідності, що проходить за проводами, приєднаними до конденсатора, переходять у лінії струму зміщення в діелектрику, утворюючи загальну замкнену лінію струму.

Конденсатор здатен зберігати свої заряди і у разі вимкнення від джерела енергії. Тому визначаючи напругу на ньому, слід урахувати його попередній стан:

,

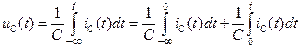де 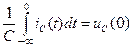– напруга на конденсаторі при .

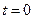Отже, 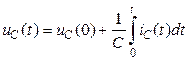. (1.9)

Якщо ємність не мала початкового заряду, то

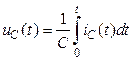. (1.10)

Миттєву потужність 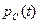та енергію 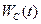накопичену в ємності, записують формулами:

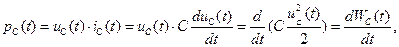(1.11)

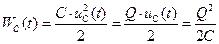, (1.12)

де 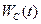– енергія електричного поля, що зосереджене в конденсаторі.

Струм безвтратного конденсатора 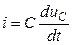. Якщо до конденсатора прикладена постійна напруга 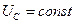, то 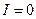. Відсутність струму в ємності у разі підведення до неї постійної напруги означає, що ємність в усталеному режимі чинить постійному струму нескінченний опір.

Зауваження! Між різним частинами електротехнічних пристроїв, що знаходяться під напругою, існують електричні поля, які створюються зарядами на поверхні цих частин. За умови роботи пристроїв на промислових частотах ці поля здебільшого слабкі, тому при аналізі процесів їх не беруть до уваги. Разом з тим, розповсюджені пристрої, в яких виникають достатньо сильні електричні поля. Урахування небажаних (паразитних) ємностей і струмів витоку через них є обов’язковим в багатьох випадках, наприклад, під час аналізу довгих лінії передавання енергії, радіотехнічних пристроїв.

Індуктивні котушки

Провідники зі струмом здатні створювати, концентрувати й утримува­ти довкола себе магнітне поле. Замкнутий контур із струмом завжди пронизується магнітним потоком, створений струмом цього контуру. При проходженні струму по котушці кожен її виток пронизує магнітний потік.

Алгебраїчна сума магнітних потоків, що пронизують витки і викликані струмом в цьому колі, є потокощепленням самоіндукції (позначається Ψ_L).

Примітка: (ракурс в теорію електромагнетизму)

Кількісно магнітне поле характеризується магнітним потоком 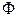, який визначається кількістю одиничних магнітних силових ліній через поверхню .

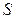Магнітний потік всередині одного витка:

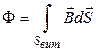(1.13)

Магнітні лінії за своєю природою завжди замкнені, тому поверхнею інтегрування 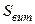може бути будь-яка поверхня, що спирається на виток.

Принцип роботи багатьох електротехнічних пристроїв синусоїдного струму (генераторів, двигунів, трансформаторів, вимірювальних приладів, тощо) заснований на використанні енергії магнітного поля, створеного у певній частині пристрою. У переважній більшості випадків застосування постійних магнітів буває економічно невиправданим, внаслідок їх значної вартості. На практиці для концентрації магнітного поля у заданій ділянці простору використовують спеціальні пристрої – індуктивні котушки (котушки індуктивності). Витки котушок намотують впритул один до одного суцільним ізольованим провідником (рис. 1.7). Котушки можуть бути без осердя (рис. 1.7, а),б)) або з осердям (рис. 1.7, в),г)).

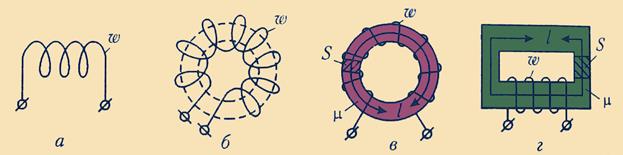
Рис. 1.7. Різні конструкції дроселів

Індуктивну котушку можна розглядати як контур зі складною поверхнею, що утворена всіма витками. Якщо через котушку проходить електричний струм, навколо неї утворюється і утримується магнітне поле (рис. 1.8).

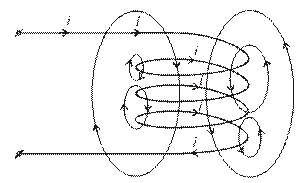
Рис. 1.8. Утворення магнітного поля під час проходження струму через котушку

В індуктивних котушках одна й та сама магнітна лінія може бути зчеплена з кількома витками. Цю обставину враховують введенням поняття потокозчеплення 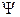, під яким розуміють потік вектора магнітної індукції через повну складну поверхню 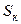, яка створена всіма витками котушки:

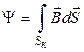(1.14)

Потокозчеплення також можна визначити як суму магнітних потоків, зчеплених з окремими витками котушки:

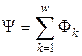(1.15)

або як суму зчеплень кожної з одиничних магнітних ліній зі своєю кількістю витків. В окремому випадку, коли всі лінії зчеплені з усіма 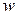витками, справедливою є формула (1.16):

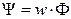(1.16)

Якщо потокозчеплення створюється власним струмом котушки, його називають потокозчепленням самоіндукції, а потік – потоком самоіндукції.

Потокозчеплення самоіндукції 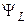залежить від геометричних розмірів 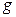котушки, магнітних властивостей середовища, в якому існує магнітний потік 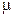, та від значення струму 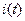: 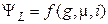. Якщо магнітна проникність середовища 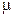і геометричні розміри котушки 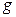незмінні, то між струмом і потокозчепленням існує лінійна залежність:

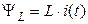
або

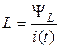, (1.17)

де 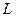– індуктивність котушки. Отже, параметр 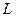кількісно оцінює співвідношення між струмом і створеним цим струмом потокозчепленням самоіндукції.

Якщо оди і той самий струм проходить по котушках різних розмірів та різної кількості витків або по різних контурах, то і потоки, які пронизують окремі витки або контури, і сума потоків, а отже і потокощеплення, будуть різними. Отже для різних котушок та контурів коефіцієнт пропорційності між потокощепленням та струмом різний. А відношення потокощеплення до струму через котушку або контур є величиною постійною та називається індуктивністю.

Під індуктивністю розуміють фізичну скалярну величину, що характе­ризує властивість контуру, в якому проходить струм, створювати та утримувати довкола себе магнітне поле (або інакше, концентрувати його у певній ділянці простору). Індуктивність дорівнює відношенню потокозчеплення самоіндукції контуру до струму, що його створює (1.17).

Одиниця індуктивності – генрі (Гн): .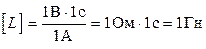

Індуктивність залежить від геометричних розмірів котушки і властивостей середовища, в якому зосереджене магнітне поле:

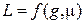(1.18)