Сумма углов треугольника равна 180 градусам.
| | Признаки параллельности прямых. | |
| | Свойства параллельных прямых. | |
| | Сумма углов треугольника | |
| | Формулы сокращенного умножения | 1) Разность квадратов 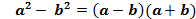 2) Разность кубов 2) Разность кубов 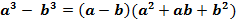 3) Сумма кубов 3) Сумма кубов 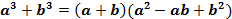 4) Квадрат суммы 4) Квадрат суммы 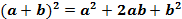 5) Квадрат разности 5) Квадрат разности 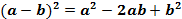 6) Куб суммы 6) Куб суммы 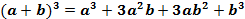 7) Куб разности 7) Куб разности 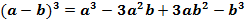 |
| | Системы уравнений и методы их решений | 1.Если в уравнениях неизвестные числа одни и те же, то эти уравнения образуют систему. Решением системы уравнений с двумя неизвестными называют такую пару чисел, которые при подстановке в эту систему обращают каждое ее уравнение в верное числовое равенство. 2.Чтобы решить систему уравнений можно применить: | Способ подстановки | Способ сложения | Графический способ | | выразить переменную из одного уравнения и подставить полученное выражение во второе уравнение | коэффициенты при одной из переменных сделать противоположными числами, выполнить сложение уравнений | построить графики обоих уравнений, найти координаты общих точек | |
| | Линейная функция. График линейной функции. | 2. Зависимость у(х) называется функцией, х – независимая переменная (аргумент), у – зависимая переменная. 3. Прямая пропорциональная зависимость у = k·х, где k – коэффициент пропорциональности. | График проходит через начало координат. | | 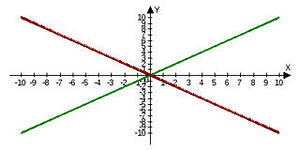 4. Линейная функция: у= k·х+в. Графиком линейной функции является прямая, значит, для построения графика достаточно построить две точки. | k- одинаковый, прямые параллельны, в =4, в=0, в=-3. Т.е. в показывает точку пересечения графика с осью Оу. | |     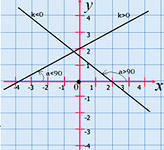 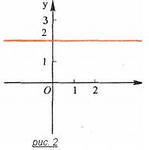 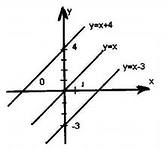 |
| | Прямоугольный треугольник. Свойства прямоугольных треугольников. | 1. Прямоугольный треугольник – треугольник, один из углов которого – прямой. Сторона, лежащая напротив прямого угла, называется гипотенузой, а стороны, заключающие прямой угол – катетами. 2. Свойства прямоугольных треугольников: а) Сумма двух острых углов прямоугольного треугольника равна 90о. б) Катет прямоугольного треугольника, лежащий напротив угла в 30о, равен половине гипотенузы. в) Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета равен 30о. |
| | Признаки равенства прямоугольных треугольников | 3. Признаки равенства прямоугольных треугольников (прямые углы и по два других, соответственно равных элемента): а) Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. б) Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого, то такие треугольники равны. в) Если гипотенуза и острый угол одного прямоугольного треугольника , соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. г) Если гипотенуза и катет одного прямоугольного треугольника , соответственно равны гипотенузе и катету другого, то такие треугольники равны. |
| | Расстояние между двумя точками; Расстояние от точки до прямой; Расстояние между двумя параллельными прямыми | Расстояние между двумя точками – длина отрезка, соединяющего эти точки. 5. Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из точки к прямой. 6. Расстоянием между двумя параллельными прямыми, считается расстояние от произвольной точки одной прямой до другой прямой. |
| | Арифметический квадратный корень из числа. Свойства ар.квадратного корня. | Определение арифметического квадратного корня.Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а. 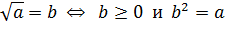 Тождество Тождество 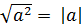 Свойства арифметического квадратного корня: 1) Свойства арифметического квадратного корня: 1) 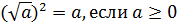 2)Корень из произведения равен произведению корней: 2)Корень из произведения равен произведению корней: 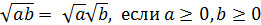 ; 3) Корень из частного равен частному корней: ; 3) Корень из частного равен частному корней: 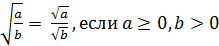 |
| | Модуль числа. Свойства модуля. | . Обозначают модуль числа так: |−4| = 4 Читают символы выше следующим образом: «модуль числа минус четыре равен четырём».     Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу. Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать, что модуль числа не может быть отрицательным. Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи. 1. Модуль положительного числа равен самому числу. |a| = a, если a > 0; 2. Модуль отрицательного числа равен противоположному числу. |−a| = a, если a < 0; 3. Модуль нуля равен нулю. |0| = 0, если a = 0; 4. Противоположные числа имеют равные модули. |−a| = |a|; Примеры модулей рациональных чисел: Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу. Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать, что модуль числа не может быть отрицательным. Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи. 1. Модуль положительного числа равен самому числу. |a| = a, если a > 0; 2. Модуль отрицательного числа равен противоположному числу. |−a| = a, если a < 0; 3. Модуль нуля равен нулю. |0| = 0, если a = 0; 4. Противоположные числа имеют равные модули. |−a| = |a|; Примеры модулей рациональных чисел: ![]() |−4,8| = 4,8 |−4,8| = 4,8 ![]() |0| = 0 |0| = 0 ![]() |−3/8| = |3/8| |−3/8| = |3/8| |
| | Множества натуральных, целых, действительных, рациональных и иррациональных чисел. Примеры чисел из каждого множества. | I. Множество всех натуральных чисел N.Натуральные числа – это числа, используемые при счете предметов. 2. Множество всех целых чисел Z.Натуральные числа, ноль и числа, противоположные натуральным. 3. Множество всех рациональных чисел Q. Целые числа и числа, которые можно записать в виде  ( m ( m 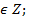 n n 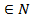 ) (обыкновенные дроби, конечные и бесконечные периодические десятичные дроби). 4. Множество всех действительных чисел R. Рациональные числа и иррациональные числа (числа, которые нельзя записать в виде обыкновенных дробей – бесконечные непериодические десятичные дроби) ) (обыкновенные дроби, конечные и бесконечные периодические десятичные дроби). 4. Множество всех действительных чисел R. Рациональные числа и иррациональные числа (числа, которые нельзя записать в виде обыкновенных дробей – бесконечные непериодические десятичные дроби) |
| | Таблица квадратов натуральных чисел до 25. | Таблица квадратов натуральных чисел от 11 до 29
|
| | Алгебраические дроби. Сложение, вычитание,умножение,деление алгебраических дробей с разными знаменателями | 5. Чтобы сложить (вычесть) алгебраические дроби, нужно: · Найти общий знаменатель дробей (произведение всех различных множителей, из которых состоят знаменатели дробей); · Привести дроби к общему знаменателю, домножив числитель и знаменатель на выбранный дополнительный множитель; · Выполнить сложение (вычитание) с числителями, знаменатель оставить без изменения; · Упростить результат, если возможно. 1.Основное свойство дроби: если числитель и знаменатель алгебраической дроби умножить или разделить на одно и то же число или выражение не равное нулю, то значение дроби не изменится. 2. Чтобы сократить дробь, надо числитель и знаменатель разделить на их общий множитель. 3. Правила действий с дробями: Сложение: Умножение: Деление 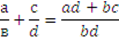 ; ; 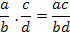 ; ; 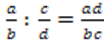 |
| | Многоугольники. Виды многоугольников. | - Сумма углов выпуклого n - угольника равна (n – 2 )·180o.
- Сумма углов выпуклого четырехугольника равна 360o.
- Параллелограмм- это четырехугольник, у которого противоположные стороны попарно параллельны.
4. Свойства параллелограмма А) В параллелограмме противоположные стороны равны и противоположные углы равны.                        Б) Диагонали параллелограмма точкой пересечения делятся пополам. Б) Диагонали параллелограмма точкой пересечения делятся пополам. | 5. Признаки параллелограмма А) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм. Б) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. В) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. | - Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие – не параллельны.
 | |    | | | равнобедренная | прямоугольная | - Прямоугольник – это параллелограмм, у которого все углы прямые.
- Особое свойство прямоугольника
Диагонали прямоугольника равны. | - Признак прямоугольника
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. | - Ромб – это параллелограмм, у которого все стороны равны.
| 11. Особое свойство ромба. Диагонали ромба взаимно перпендикулярны и делят его углы пополам. |     | - Квадрат – это прямоугольник, у которого все стороны равны.
|
| | Площадь квадрата, прямоугольника, треугольника, трапеции, параллелограмма. | Формулы площадей Треугольник Площадь треугольника равна половине произведения его основания  на высоту. h на высоту. h 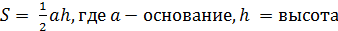 a Параллелограмм Площадь параллелограмма равна произведению его основания на высоту. a Параллелограмм Площадь параллелограмма равна произведению его основания на высоту.  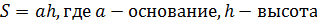 h a Прямоугольник Площадь прямоугольника равна произведению его смежных сторон. h a Прямоугольник Площадь прямоугольника равна произведению его смежных сторон. 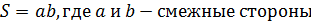  a b Трапеция Площадь трапеции равна a b Трапеция Площадь трапеции равна  произведению полусуммы ее оснований на высоту. произведению полусуммы ее оснований на высоту. 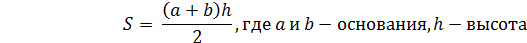 b h a b h a |
| | Теорема Пифагора. Формулировка и примеры. |   В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. a c В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. a c 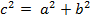  b b |
| | § 17. Функция у = кх2 ,ее свойства и график | Функция у = kx2 (k > 0) ограничена снизу и не ограничена сверху. Область значений функции — луч [0; +°°). Функция выпукла вниз. Свойства функции у = kx2 при k < 0 (рис. 44) Область определения функции — (-°°; +°°). У = 0 при х = 0; у < 0 при х Ф 0. У = kx2 — непрерывная функция. I/наиб = 0 (достигается при х = 0), ука„к не существует. Функция возрастает при х < 0 и убывает при х > 0. Функция ограничена сверху и не ограничена снизу. График постройте самостоятельно по точкам! |
| | § 18. Фукция у = k/x, её свойства и график | 3) Функция у=  и ее график Функция определена при х и ее график Функция определена при х 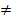 0, принимает все значения, кроме 0. График функции – гипербола. 0, принимает все значения, кроме 0. График функции – гипербола. 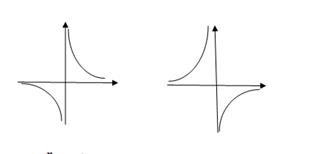 |
| | Построение графиков функций с помощью сдвигов относительно осей. |  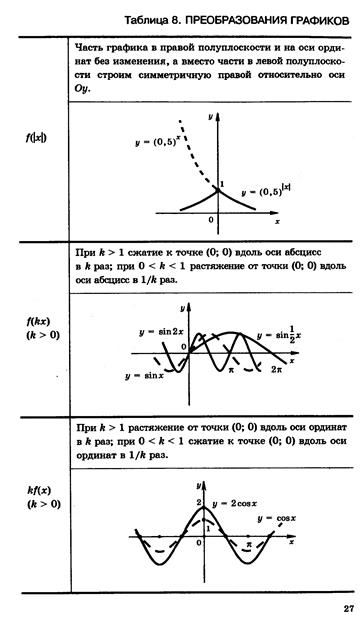 |
| | § 22. Функция у=aх2 + bх + c, ее свойства и график | | Четверть | | | Предмет | алгебра | | Класс | | 1. Функция y = 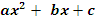 и ее график и ее график График функции y = 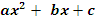 - парабола. - парабола. 2. Алгоритм построения графика функции y = 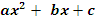 1)Найти координаты вершины параболы: 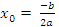 , , 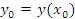 . . 2)Провести ось симметрии х= 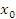 3) Определить направление «ветвей» параболы 4) Найти координаты точек пересечения графика с осью ОХ (нули функции). Для этого решить уравнение у = 0, т.е. 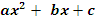 = 0. = 0. 5) Найти координаты точки пересечения графика с осью ОУ: х=0,у=с ; (0; с). 6) Найти координаты дополнительных точек. 7) Построить найденные пять точек и провести через них параболу. |
| | Квадратное уравнение. § 25. Формула корней квадратных уравнений | 3. Решение квадратного уравнения 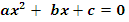 , где a , где a 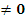 Дискриминант квадратного уравнения D = Дискриминант квадратного уравнения D = 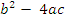 ; ; 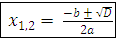  4. Зависимость количества корней квадратного уравнения от дискриминанта 4. Зависимость количества корней квадратного уравнения от дискриминанта | D > 0 | D = 0 | D < 0 | | Два различных действительных корня | Один (два равных) действительный корень | Нет действительных корней | 5. Решение задачи с помощью уравнения проводится в 3 этапа: 1) Запись условия и выбор неизвестного , обозначаемого буквой, 2) Составление уравнения и его решение, 3) Объяснение полученных в результате решения уравнения чисел с точки зрения условия задачи. |
| | Теорема Виетта. Теорема, обратная теореме Виетта. Разложение квадратного трехчлена на множители. | 1. Теорема Виета Для полного квадратного уравнения 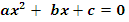 | Для приведенного квадратного уравнения  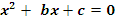 | Если 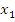 и и 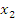 – корни уравнения – корни уравнения 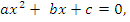 то то 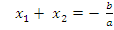 и и 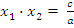 | Если 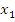 и и 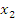 – корни уравнения – корни уравнения 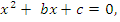 то то 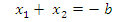 и и 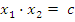 | 2. Разложение квадратного трехчлена на множители: 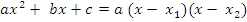 , где , где 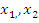 - корни квадратного трехчлена - корни квадратного трехчлена 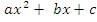 |
| | Решение задач с помощью уравнений. | Решение задачи с помощью уравнения проводится в 3 этапа: 4) Запись условия и выбор неизвестного , обозначаемого буквой, 5) Составление уравнения и его решение, 6) Объяснение полученных в результате решения уравнения чисел с точки зрения условия задачи. |
| | § 30. Иррациональные уравнения | |
| | § 31. Свойства числовых неравенств | 5. Алгоритм решения неравенств f(x) >0 (f(x) <0)методом интервалов: 1) найти значения х , при которых левая часть неравенства обращается в нуль (числитель и знаменатель обращается в нуль) 2) отметить полученные значения на числовой прямой, соответствующие точки могут быть закрашенные ( 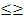 ) или нет ( ) или нет ( 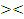 , так же точки из знаменателя) 3) на полученных числовых промежутках определить знак выражения левой части f(x) 4) выбрать промежутки, соответствующие знаку неравенства (+ , так же точки из знаменателя) 3) на полученных числовых промежутках определить знак выражения левой части f(x) 4) выбрать промежутки, соответствующие знаку неравенства (+ 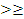 ; ; 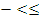 ) 5) записать ответ. ) 5) записать ответ. |
| | § 32. Исследование функций на монотонность | |
| | § 33. Решение линейных неравенств |  |
| | § 34. Решение квадратных неравенств |  |
| | Определение подобных треугольников. Признаки подобия треугольников. | b Подобные треугольники Определение.Два треугольника называются подобными, если углы одного треугольника соответственно равны углам другого треугольника, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.   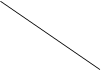  A M ABC A M ABC 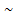 MKP⟺ MKP⟺ 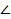 A=∠M, ∠B=∠K, ∠C=∠P и A=∠M, ∠B=∠K, ∠C=∠P и   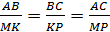 = k (коэффициент подобия) B C K P Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников 1 признак.Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. Если = k (коэффициент подобия) B C K P Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников 1 признак.Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. Если 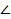 A=∠M, ∠B=∠K, то ABC A=∠M, ∠B=∠K, то ABC 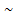 MKP (см.рис.к определению) 2 признак. Если две стороны одного треугольника пропорциональны двум сходственным сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны. Если MKP (см.рис.к определению) 2 признак. Если две стороны одного треугольника пропорциональны двум сходственным сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны. Если 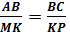 и ∠B=∠K , то ABC и ∠B=∠K , то ABC 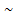 MKP (см.рис.к определению) 3 признак.Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого треугольника, то такие треугольники подобны. Если MKP (см.рис.к определению) 3 признак.Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого треугольника, то такие треугольники подобны. Если 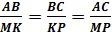 , то ABC , то ABC 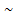 MKP (см.рис.к определению) MKP (см.рис.к определению) |
| | Соотношения между сторонами и углами прямоугольного треугольника | Обязательный минимум | Четверть | | | Предмет | геометрия | | Класс | |  А А
b c С а В Наши рекомендации |
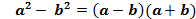 2) Разность кубов
2) Разность кубов 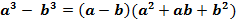 3) Сумма кубов
3) Сумма кубов 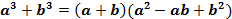 4) Квадрат суммы
4) Квадрат суммы 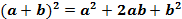 5) Квадрат разности
5) Квадрат разности 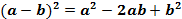 6) Куб суммы
6) Куб суммы 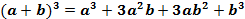 7) Куб разности
7) Куб разности 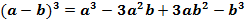








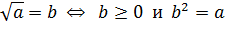 Тождество
Тождество 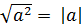 Свойства арифметического квадратного корня: 1)
Свойства арифметического квадратного корня: 1) 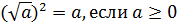 2)Корень из произведения равен произведению корней:
2)Корень из произведения равен произведению корней: 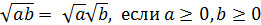 ; 3) Корень из частного равен частному корней:
; 3) Корень из частного равен частному корней: 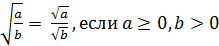



 Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу. Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать, что модуль числа не может быть отрицательным. Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи. 1. Модуль положительного числа равен самому числу. |a| = a, если a > 0; 2. Модуль отрицательного числа равен противоположному числу. |−a| = a, если a < 0; 3. Модуль нуля равен нулю. |0| = 0, если a = 0; 4. Противоположные числа имеют равные модули. |−a| = |a|; Примеры модулей рациональных чисел:
Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу. Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать, что модуль числа не может быть отрицательным. Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи. 1. Модуль положительного числа равен самому числу. |a| = a, если a > 0; 2. Модуль отрицательного числа равен противоположному числу. |−a| = a, если a < 0; 3. Модуль нуля равен нулю. |0| = 0, если a = 0; 4. Противоположные числа имеют равные модули. |−a| = |a|; Примеры модулей рациональных чисел:  ( m
( m 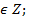 n
n 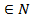 ) (обыкновенные дроби, конечные и бесконечные периодические десятичные дроби). 4. Множество всех действительных чисел R. Рациональные числа и иррациональные числа (числа, которые нельзя записать в виде обыкновенных дробей – бесконечные непериодические десятичные дроби)
) (обыкновенные дроби, конечные и бесконечные периодические десятичные дроби). 4. Множество всех действительных чисел R. Рациональные числа и иррациональные числа (числа, которые нельзя записать в виде обыкновенных дробей – бесконечные непериодические десятичные дроби) 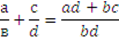 ;
; 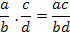 ;
; 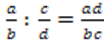

















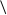



 Б) Диагонали параллелограмма точкой пересечения делятся пополам.
Б) Диагонали параллелограмма точкой пересечения делятся пополам. 







 на высоту. h
на высоту. h 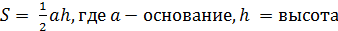 a Параллелограмм Площадь параллелограмма равна произведению его основания на высоту.
a Параллелограмм Площадь параллелограмма равна произведению его основания на высоту. 
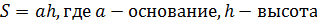 h a Прямоугольник Площадь прямоугольника равна произведению его смежных сторон.
h a Прямоугольник Площадь прямоугольника равна произведению его смежных сторон. 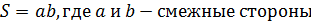
 a b Трапеция Площадь трапеции равна
a b Трапеция Площадь трапеции равна  произведению полусуммы ее оснований на высоту.
произведению полусуммы ее оснований на высоту. 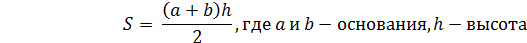 b h a
b h a 
 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. a c
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. a c 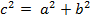
 b
b  и ее график Функция определена при х
и ее график Функция определена при х 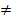 0, принимает все значения, кроме 0. График функции – гипербола.
0, принимает все значения, кроме 0. График функции – гипербола. 


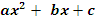 и ее график
и ее график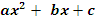 - парабола.
- парабола.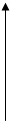

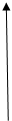

 с
с 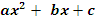
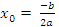 ,
, 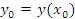 .
.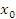
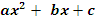 = 0.
= 0.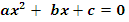 , где a
, где a 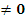 Дискриминант квадратного уравнения D =
Дискриминант квадратного уравнения D = 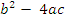 ;
; 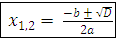
 4. Зависимость количества корней квадратного уравнения от дискриминанта
4. Зависимость количества корней квадратного уравнения от дискриминанта 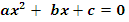

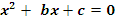
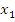 и
и 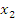 – корни уравнения
– корни уравнения 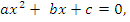 то
то 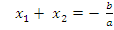 и
и 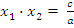
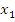 и
и 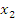 – корни уравнения
– корни уравнения 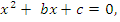 то
то 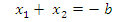 и
и 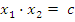
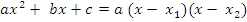 , где
, где 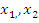 - корни квадратного трехчлена
- корни квадратного трехчлена 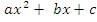
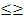 ) или нет (
) или нет ( 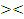 , так же точки из знаменателя) 3) на полученных числовых промежутках определить знак выражения левой части f(x) 4) выбрать промежутки, соответствующие знаку неравенства (+
, так же точки из знаменателя) 3) на полученных числовых промежутках определить знак выражения левой части f(x) 4) выбрать промежутки, соответствующие знаку неравенства (+ 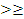 ;
; 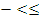 ) 5) записать ответ.
) 5) записать ответ. 




 A M ABC
A M ABC 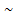 MKP⟺
MKP⟺ 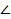 A=∠M, ∠B=∠K, ∠C=∠P и
A=∠M, ∠B=∠K, ∠C=∠P и 

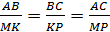 = k (коэффициент подобия) B C K P Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников 1 признак.Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. Если
= k (коэффициент подобия) B C K P Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников 1 признак.Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. Если 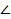 A=∠M, ∠B=∠K, то ABC
A=∠M, ∠B=∠K, то ABC 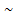 MKP (см.рис.к определению) 2 признак. Если две стороны одного треугольника пропорциональны двум сходственным сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны. Если
MKP (см.рис.к определению) 2 признак. Если две стороны одного треугольника пропорциональны двум сходственным сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны. Если 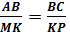 и ∠B=∠K , то ABC
и ∠B=∠K , то ABC 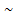 MKP (см.рис.к определению) 3 признак.Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого треугольника, то такие треугольники подобны. Если
MKP (см.рис.к определению) 3 признак.Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого треугольника, то такие треугольники подобны. Если 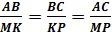 , то ABC
, то ABC 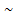 MKP (см.рис.к определению)
MKP (см.рис.к определению)  А
А