Исключаем значения угла a , при которых знаменатель дроби sin a

обращается в нуль: sin a ¹ 0; a ¹ p k , k Î Z ;

Ответ: a ¹ p k , k Î Z .

Упражнения:

№1. Вычислить значения остальных тр. функций, если известно значение cos a = - , .

№2. Вычислить значения остальных тр. функций, если известно значение сtg a = - 2,5 , .

№3. Вычислить:

а) tg a , если sin a = и ; б) cos a , если сtg a = и .

№4. Упростить выражение:

а) ; г) ;

б) ; д) ;

в) ; е) .

№5. Доказать тождество, указав область допустимых значений:

а) ; г) ;

б) ; д) ;

в) ; е) .

№6. Доказать, что при всех допустимых значениях a значение выражения не зависит от a :

1) ; 2) ; 3) .

№7. Найти наибольшее и наименьшее значения выражения:

1) 1 – (cos ²a –- sin ²a ) ; 3) cos ²a · tg ²a + 5 cos ²a – 1 ;

2) 1 – sin a · cos a · tg a ; 4) sin a + 3sin ²a + 3cos ²a .

№8. Доказать тождество:

1) (sin b + sin a ) · ( sin a - sin b ) - (cos a + cos b ) · (cos b – cos a ) = 0;

2) ctg ² a - cos²a = ctg ² a · cos²a ;

3) ;

4) .

8. Периодичность тригонометрических функций.

Определение: Функция называется периодической, если существует число T ¹ 0, прибавление которого к любому значению аргумента не меняет значения функции, то есть для любого x из области определения функции выполняется равенство .

Число T называется периодом функции .

Определение: Наименьший среди положительных периодов функции называется основным периодом функции.

Теорема: Синус и косинус являются периодическими функциями с основным периодом 2p.

sin a = sin (a + 2p ) при a Î (- ∞ ; + ∞)

cos a = cos (a + 2p ) при a Î (- ∞ ; + ∞)

Теорема: Тангенс и котангенс являются периодическими функциями с основным периодом p.

tg a = tg (a + p )

y

x

N

M

- x

y

a

a + p

A

- y

x

ctg a = ctg (a + p ) для любых допустимых значений a .

x

A

y

a

x

M

y

Справедлива следующая теорема.

Теорема: К аргументу любой тригонометрической функции можно прибавлять любое целое число периодов. Из аргумента любой тригонометрической функции можно вычитать любое целое число периодов.

sin a = sin (a + 2pк) , к Î Z tg a = tg (a + pк) , к Î Z

cos a = cos (a + 2pк) , к Î Z ctg a = ctg (a + pк) , к Î Z

9. Четность, нечетность тригонометрических функций

Определение: Функция называется четной, если противоположным значениям аргумента x и – x из области определения соответствует одно и то же значение функции, то есть .

Определение: Функция называется нечетной, если противоположным значениям аргумента x и – x из области определения соответствуют противоположные значения функции, то есть .

y

x

N

M

y

a

A

-y

-x

-a

Теорема: Синус, тангенс и котангенс являются нечетными функциями, косинус является четной функцией.

sin (– a) = –sina , ctg (– a) = – ctga ,

tg (– a) = – tga , cos (– a) = cos a

для всех допустимых значений a .

Пример:

№1. Найти значения тригонометрических функций:

1) cos 10p ; 2) sin 7p ; 3) ; 4) ctg (– 3570º) .

Решение:

1) cos 10p = cos (10p –2p ·5) = cos 0 = 1;

2) sin 7p = sin (7p – 2p ·3) = sin p = 0;

3) ;

4) ctg (– 3570º) = –ctg 3570º =– ctg (3570º – 180º·19) =– ctg (150º–180º) =

= –ctg (–30º) =ctg 30º = .

№2. Вычислить значение выражения: .

Решение:

1. ;

2. ;

3. ;

4.

5. .

Ответ: .

Упражнения:

№1. Вычислить:

1) ; 3) ;

2) ; 4) ;

5) .

№2. Найти значение выражения А :

1) ;

2) ;

3) .

10. Тригонометрические функции суммы и разности двух аргументов.

10.1.

x

y

A

M

x1

y1

N

y2

x2

Косинус и синус суммы и разности двух аргументов.

Рассмотрим в .

ОА- начальный радиус .

- радиус-вектор точки М (x₁; y₁ ), принадлежащей

. a = Ð (ОА , ОМ ) = Ð AO М.

- радиус-вектор точки N (x₂ ; y₂ ), принадлежащей . b = Ð (ОА , ОN ) = Ð AO N.

j = a - b = Ð (ОМ , ОN ) = Ð М O N .

Так как уголj = a - b образован векторами (x₁; y₁ ) и (x₂ ; y₂ ) , воспользуемся формулой :

cos (a - b ) = cos a · cos b + sin a · sin b

Косинус разности двух углов равен сумме произведений косинусов данных углов и синусов данных углов.

Пример: Вычислить cos 15°.

Решение: Представим угол 15° в виде разности углов 45° и 30° , воспользуемся формулой косинуса разности двух углов:

cos (a - b) = cos a · cos b + sin a · sin b

cos 15° = cos (45° - 30°) = cos 45° · cos 30° + sin 45° · sin 30° =

Ответ: cos 15° = 0,945.

cos (a + b) = cos a · cos b - sin a · sin b

Косинус суммы двух углов равен разности произведений косинусов данных углов и синусов данных углов.

Пример: Вычислить cos 75°.

Решение: cos 75° = cos (45° + 30° ) = cos 45° · cos 30° - sin 45° · sin 30° =

Ответ: cos 75° = 0,245.

sin (a + b) = sin a · cos b + cos a · sin b

Синус суммы двух углов равен сумме произведений синуса первого угла на косинус второго угла и косинуса первого угла на синус второго угла.

sin (a - b) = sin a · cos b - cos a · sin b

Синус разности двух углов равен разности произведений синуса первого угла на косинус второго угла и косинуса первого угла на синус второго угла.

Пример: Вычислить sin (a + b ) , если sin a = , cos b = , < a < p , 0 < b < .

Решение:

Для вычисления sin (a + b) по формуле sin (a + b) = sin a · cos b + cos a · sin b необходимо найти cos a и sin b . Воспользуемся формулой sin ² a + cos ² a = 1 .

cos ² a = 1 - sin ² a ; sin ² b = 1 - cos ² b ;

; так как < a < p , cos a < 0 .

sin b = ; так как 0 < b < , sin b > 0 .

.

Ответ: .

Упражнения:

№1. Вычислить: 1) sin 15° ; 3) cos 107° cos 17° + sin 107° sin 17° ;

2) sin 75° ; 4) sin 57° cos 12° - cos 57° sin 12° .

№2. Упростить:

1) sin 2b · cos b + cos 2b · sin b; 2) sin (a + b)- sin a · cos b ;

3) sin ( +a )- cos a ; 4) ;

5) sin ( +a ) · cos (a - ) + cos ( +a ) · sin (a - ) ;p < a < ,

6) cos (30° + a ) - cos (30° - a ) .

№3. Вычислить cos ( - a ) , если tg a = 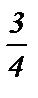, p < a < .

№4. Проверить равенство:

а) sin (90° +a ) = cos a ; б) cos (180° +a ) = - cos a ; в) cos (270° -a ) = - sin a .

№5. Упростить:

1) 2) .