Простейшие операции с матрицами
Проверочная работа
Вычислить значение итоговой стоимости и построить диаграмму. Установите формат (денежный)
| Товар | Цена (в рублях) | Кол-во | Итог |
| 8,98 |
2. Построить график функции y=cos(x)-x для х -10 до 10 с шагом 1
Построить график функции
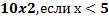
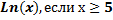
Построения поверхности z=3x+y-5
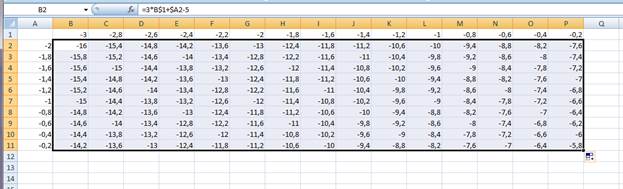
Заполним строку значений аргумента Х, начиная с ячейки В1 (хє [-3;0], шаг=0,2 → автозаполнение).
Заполним столбец значений аргумента У, начиная с ячейки А2 (ує [-2;0], шаг=0,2 → автозаполнение по столбцу).
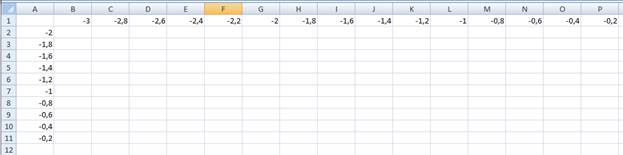
В ячейку В10 запишем формулу: =3*B$1+$A2-5 (знак $ нужен для того, чтобы зафиксировать строку).
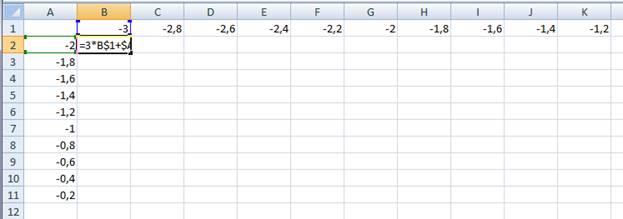
Скопируем эту формулу на все ячейки диапазона B2:Р11 (автозаполнение по столбцу и по строке).
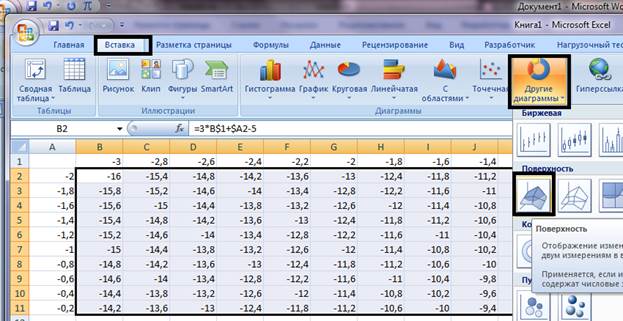
Не снимая выделение с диапазона, вызовем Мастер диаграмм с помощью команды Вставка /Другие диаграммы / поверхность.
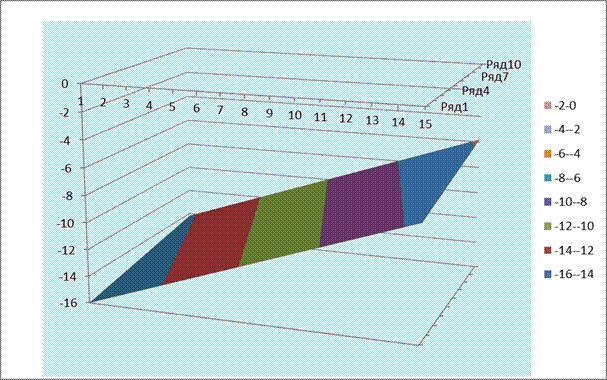
Результат
Построить верхнюю часть эллипсоида:
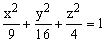
Для построения поверхности необходимо разрешить заданное уравнение относительно переменной z.
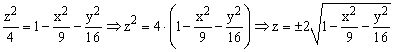 |
Так как в условии речь идет о верхней части эллипсоида, то рассмотрим ОДЗ положительной части уравнения:
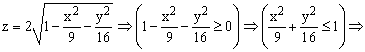 | |
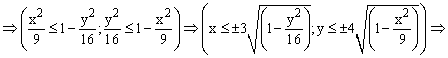 | |
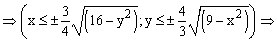 | 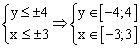 |
Приступим к построению поверхности. В диапазон B1:J1 введем последовательность значений переменной y: -4, -3, …,4, а в диапазон ячеек А2:А14 последовательность значений переменой x: -3, -2,5,…3.
В ячейку В2 введем формулу = 2*(1-($A2^2)/9-(B$1^2)/16)^0,5 и скопируем результат
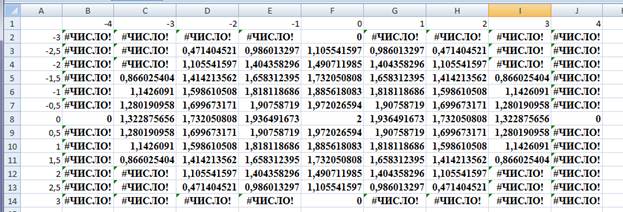
Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой - абсолютную ссылку на строку с этим именем. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:J14 в них будет найдено значение z при соответствующих значениях x, y. Т.о. создается таблица значений z.
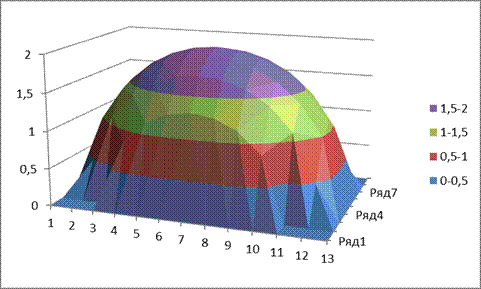
Далее построим поверхность
Задание для самостоятельной работы
Построить часть эллипсоида, заданного уравнением:
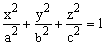 Для а=1, b=2, с=3 Для а=1, b=2, с=3 |
Построить поверхность z = x2-y2 при x, y [-1;1].
Простейшие операции с матрицами
Как и над числами, над матрицами можно проводить ряд операций, причём в случае с матрицами некоторые из операций являются специфическими.
Транспонирование
Транспонированной называется матрица (АТ), в которой столбцы исходной матрицы (А) заменяются строками с соответствующими номерами.
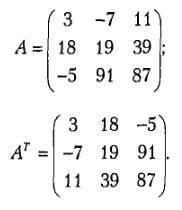
Для осуществления транспонирования в Excel используется функция ТРАНСП, которая позволяет поменять ориентацию массива на рабочем листе с вертикальной на горизонтальную и наоборот.
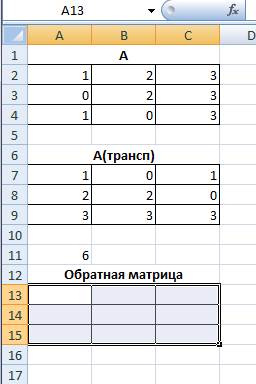
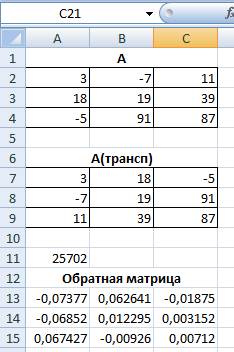
1. Введем данную матрицу в Excel
Для объединения ячеек необходимо выделить диапазон ячеек и щелкнуть правой кнопкой мыши /Формат ячеек / Выравнивание / Объединение ячеек
Выделите диапазон ячеек для транспонированной матрицы.
Далее воспользуемся командой Формулы /Ссылки и массивы /ТРАНСП
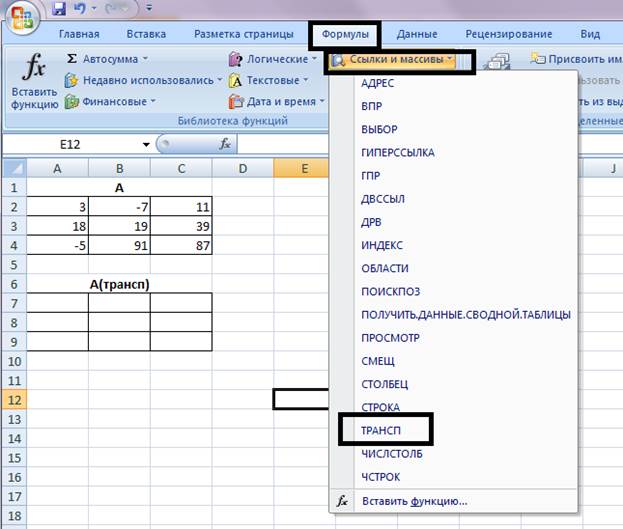
Далее выделите первый массив.
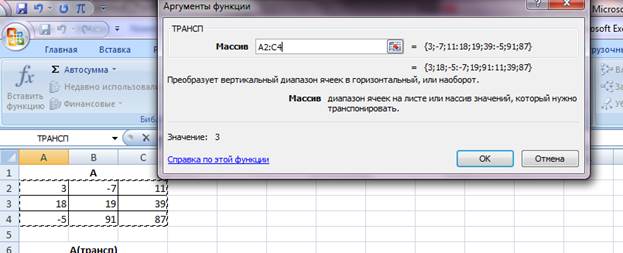
Нажмите CTRL+SHIFT+ENTER
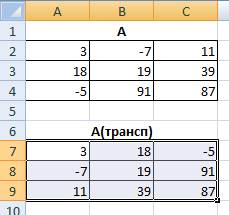
У вас получится результат
Вычисление определителя матрицы
Важной характеристикой квадратных матриц является их определитель. Определитель матрицы – это число, вычисляемое на основе значений элементов массива. Определитель матрицы А обозначается как |А| или ∆.
Определителем матрицы первого порядка А = (а11), или определителем первого порядка, называется элемент а11.
∆1 = |А| = а11
Определителем матрицы второго порядка А = (aij), или определителем второго порядка, называется число, которое вычисляется по формуле:
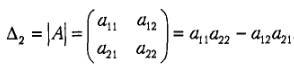
Произведения а11а22 и а12а21 называются членами определителя второго порядка.
С ростом порядка матрицы n резко увеличивает число членов определителя (n!). Например, при n=4 имеем 24 слагаемых. Существуют специальные правила, облегчающие вычисление определителей вручную, учитываются свойства определителей и т. п. При применении компьютера в использовании этих приемов нет необходимости.
В MS Excel для вычисления определителя квадратной матрицы используется функция МОПРЕД.
Для массива А1:С3, состоящего из трёх строк и трёх столбцов (матрица размером 3×3), определитель вычисляется следующим образом:
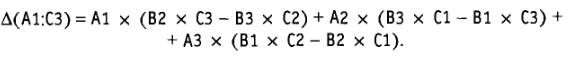
Вычислим определитель данной матрицы
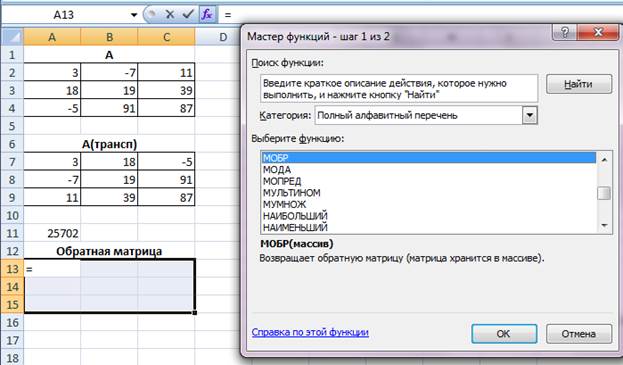
Табличный курсор поставьте в ячейку, в которую требуется получить значение определителя, например, А11, выберем команду Формулы / Вставить функции / Полный алфавитный список / МОПРЕД. После этого щелкните на кнопке ОК.
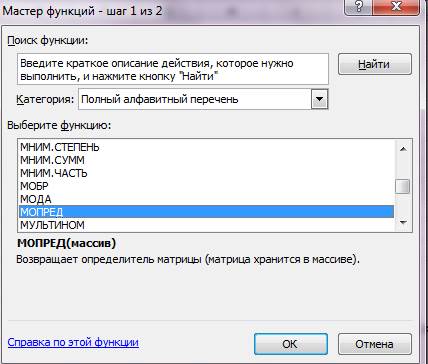
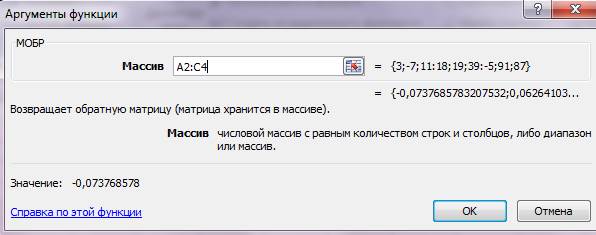
В появившееся диалоговое окно МОПРЕД мышью отодвиньте от исходной матрицы и введите диапазон исходной матрицы А2:С4 в рабочее поле Массив (указателем мыши при нажатой левой кнопке) .
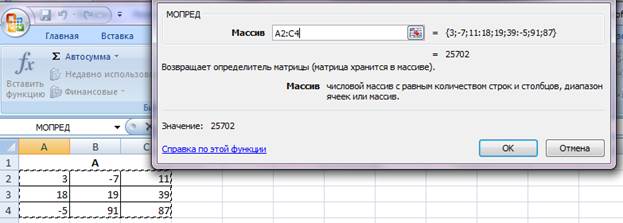
Нажмите CTRL+SHIFT+ENTER. Результат 25702
Нахождение обратной матрицы.
Для каждого числа а≠0 существует обратное число а-1, и для квадратных матриц вводится аналогичное понятие. Обратные матрицы обычно используются для решения систем уравнений с несколькими неизвестными.
Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как слева, так и справа получается единичная матрица:
как следует из определения, обратная матрица является квадратной того же порядка, что и исходная матрица.
Необходимым и достаточным условием существования обратной матрицы является невырожденность исходной матрицы. Матрица называется невырожденной или неособенной, если её определитель отличен от нуля (|А|≠0); в противном случае (|А|=0) матрица называется вырожденной или особенной.
Существуют специальные достаточно сложные алгоритмы для ручного вычисления обратных матриц. В качестве примера того, как вычисляется обратная матрица, рассмотрим квадратную матрицу второго порядка
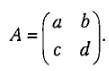
Тогда обратная матрица вычисляется следующим образом:
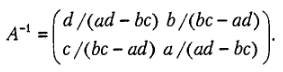
В MS Excel для нахождения обратной матрицы используется функция МОБР, которая вычисляет обратную матрицу для матрицы, хранящейся в таблице в виде массива.
Для вычисления обратной матрицы необходимо
1. Выделить блок ячеек под обратную матрицу
2. Выберите функции МОБР. После этого щелкните на кнопке ОК и выберите исходный массив
4. Нажмите сочетание клавиш CTRL+SHIFT+ENTER .
Сложение и вычитание матриц
Складывать (вычитать) можно матрицы одного размера. Суммой матриц А = (aij) и В = (bij) размера m×n называется матрица C = A + B, элементы которой cij = aij + bij для i = 1,2, …, m; j = 1,2, …, n (то есть матрица складывается поэлементно). Например, если:
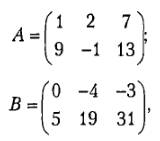
то С = А + В:
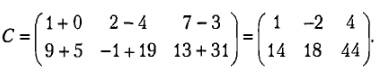
В частном случае А + 0 = А.
Аналогично определяют разность двух матриц С = А – В.
В MS Excel для выполнения операций суммирования и вычитания матриц могут быть использованы формулы, вводимые в соответствующие ячейки.
Умножение матрицы на число
Произведением матрицы А на число k называется матрица В = kA, элементы которой bij = kaij для I = 1,2, …, m; j = 1,2, …, n. Иначе говоря, при умножении матрицы на постоянную каждый элемент этой матрицы умножается на эту постоянную: k*Aij = (k*aij).
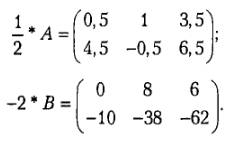 Например, для матриц А и В из предыдущего примера:
Например, для матриц А и В из предыдущего примера:
В частности, произведение матрицы А на число 0 есть нулевая матрица, то есть 0 × А = 0.
В MS Excel для выполнения операции умножения матрицы на число могут быть использованы формулы, вводимые в соответствующие ячейки.
Умножение матриц
Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй.
Пусть А = (aij) m×n, B = (bij) n×p, тогда размерность произведения А×В равна m×p. При этом матрица С называется произведением матриц А и В, если каждый её элемент cij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В:
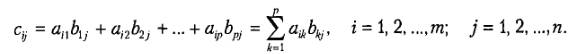 Таким образом, перемножение матриц осуществляется по следующему правилу:
Таким образом, перемножение матриц осуществляется по следующему правилу:

Функция имеет вид МУМНОЖ(массив1;массив2).
Здесь массив1 и массив2 – это перемножаемые массивы. При этом количество столбцов аргумента массив1 должно быть таким же, как количество строк аргумента массив2, и оба массива должны содержать только числа. Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.
Массив С, который является произведением двух массивов А и В, определяется следующим образом:
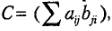
где I – номер строки, а j – номер столбца.
Рассмотрим реализацию данных операций. Заготовьте форму
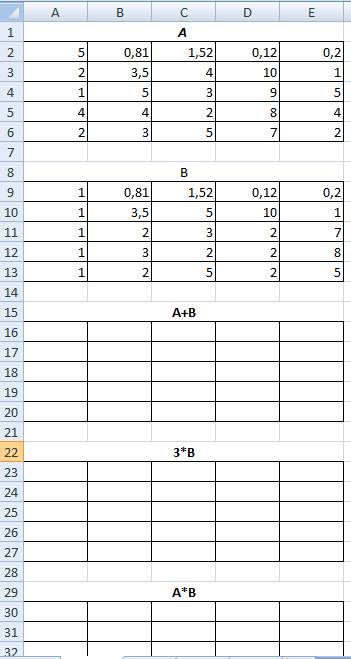
Для сложения матрицы введите формулу и скопируйте результат
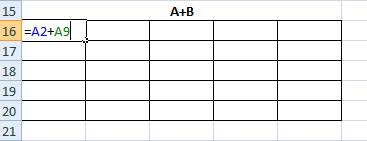
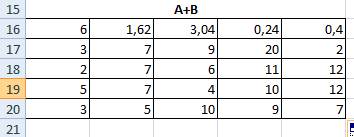
Аналогично для умножения матрицы на число
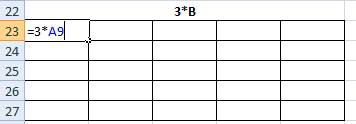
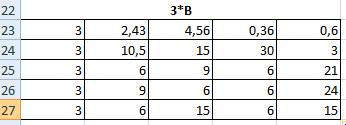
Для умножения воспользуемся функцией МУМНОЖ
Выделим искомый диапазон ячеек
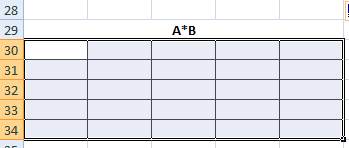
Выберите функцию МУМНОЖ и в появившееся диалоговое окно введите диапазон исходной матрицы А в рабочее поле Массив1 (указателем мыши при нажатой левой кнопке), а диапазон матрицы В введите в рабочее поле Массив2. Нажмите сочетание клавиш CTRL+SHIFT+ENTER.
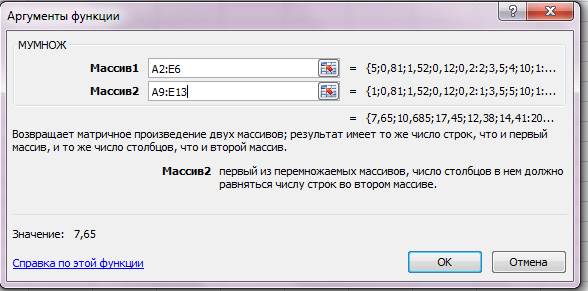
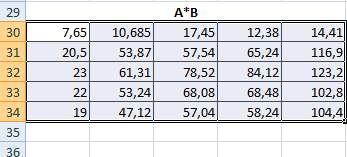
Результат
Дополнительные функции находятся на вкладке Ссылки и массивы.
Задание для самостоятельной работы
Для матриц
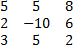
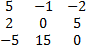
найдите обратные матрицы, определители, транспонированные, умноженные на число 5, сложение и умножение данных матриц.
