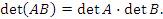II. Определитель (у квадратной матрицы)
Матрицы и определители
I. Операции над матрицами и их свойства
1. Сложение матриц. Операция сложения вводится только для матриц одинаковых размеров.
1) А + В = В + А (переместительное свойство);
2) (А + В)+С = А + (В +С) (сочетательное свойство);
3) А + 0 = А (роль нулевой матрицы).
Умножение матрицы на число.
1) (ab) х А = a х (bА) (сочетательное свойство относительно числового множителя);
2) a(А + В) = aА + aВ (распределительное свойство относительно суммы матриц);
3) (a + b) А = aА + bА (распределительное свойство относительно суммы чисел);
4) 1хА = А (роль числового множителя 1);
5) 0хА = 0 (роль нуля).
Умножение матрицы на матрицу.
Произведение АВ существует только тогда, когда число столбцов матрицы А равно числу строк матрицы В (такие матрицы называются согласованными). Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата
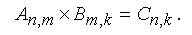
Рассмотрим умножение матриц на примере :
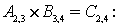
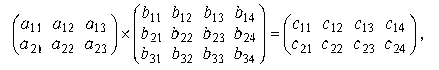
где
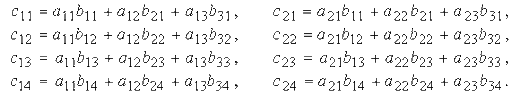
Вообще говоря АВ≠ВА, если АВ=ВА, то матрицы А и В называются перестановочными или коммутирующими.
Если А и Е – квадратные матрицы одного и того же порядка, то АЕ=ЕА=А.
Транспонирование матриц.
Матрица, полученная из данной матрицы А путем замены строк столбцами с сохранением порядка следования элементов, называется транспонированием и обозначается:
АТ(Аt, A').
Свойства операций транспонирования:
1. Amxnó ATnxm
2. (AT)T=A
3. (LA)T=LAT
(A+B)T=AT+BT
4. (AB)T=ATBT
Элементарные преобразования матриц.
1. Перестановка местами двух строк (столбцов) матрицы.
2. Умножение всех элементов данной строки (столбца) матрицы на число λ≠0.
3. Прибавление ко всем элементам данной строки (столбца) матрицы соответствующих элементов другой ее строки (столбца), умноженных на одно и то же число.
Если матрицы получены друг из друга с помощью элементарных преобразований, то они называются эквивалентными и обозначаются A~B.
Теорема:с помощью элементарных преобразований любая матрица А может быть приведена к ступенчатому виду.
Обратная матрица.
Обратная матрица существует только для квадратных матриц, определитель которых ≠0.
Если АВ=ВА=Е, то В – матрица, обратная к А и обозначается А-1.
А-1= 1/detA.
Считаем каждый элемент (А11=(-1)1+1 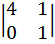 =4. И так далее, потом записываем новую матрицу, обратную А.
=4. И так далее, потом записываем новую матрицу, обратную А.
II. Определитель (у квадратной матрицы)
Любой квадратной матрице А порядка n можно поставить в соответствие число, называемое определителем или детерминантом. Число n при этом называется порядком определителя.
Правила вычисления определителя:
1. n=1. А =(а11); 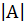 = а11
= а11
2. n=2. А = 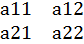 ;
; 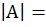 а11* а22- а12* а21
а11* а22- а12* а21
3. n=3. Правило треугольников.
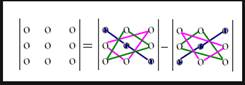
a11·a22·a33 + a12·a23·a31 + a13·a21·a32 - a13·a22·a31 - a11·a23·a32 - a12·a21·a33
| 4. Определители 4-го порядка. Методы их вычисления Теорема Лапласа. Определитель квадратной матрицы А равен сумме произведений элементов любой строки (столбца) этой матрицы на их алгебраическое дополнение. |
Определение.Выражение 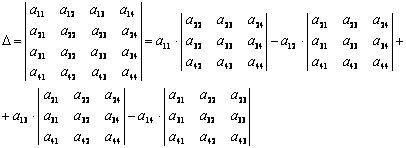 называется определителем 4-го порядка. Этот определитель можно записать в виде: называется определителем 4-го порядка. Этот определитель можно записать в виде: 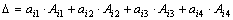 , (1.6) Аij = (-1)i+j Mij , где Аij- алгебраическое дополнение aij , Mij – минор элемента aij квадратной матрицы Аnxn (определитель порядка n-1 той матрицы, которая получается из матрицы А, путем вычеркивания i-той строки и j-того столбца). , (1.6) Аij = (-1)i+j Mij , где Аij- алгебраическое дополнение aij , Mij – минор элемента aij квадратной матрицы Аnxn (определитель порядка n-1 той матрицы, которая получается из матрицы А, путем вычеркивания i-той строки и j-того столбца). |
Свойства определителей:
1. При перестановке местами двух строк (столбцов) определитель меняет знак.
2. Если у определителя есть нулевая строка (столбец), то он равен «0».
3. Если две строки (столбца) матрицы пропорциональны или равны между собой, то определитель этой матрицы равен «0».
4. Определитель треугольной матрицы равен произведению элементов, находящихся на главной диагонали.
5. Общий множитель элементов строки (столбца) можно выносить за знак определителя(Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножению определителя на это число).
6. Определитель транспонированной матрицы равен определителю исходной матрицы:
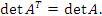
7. Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и то же число.
8. Определитель единичной матрицы =1 (на главной диагонали «1», а остальные «0»).
9. Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей: