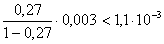Метод простой итерации

Пусть система линейных уравнений Ах = в (1) каким- либо образом приведена к виду х = Сх + f (2), где С – некоторая матрица, f – вектор- столбец. Исходя из произвольного вектора

х₀ = 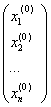, строим итерационный процесс:

х^(k+1) = cx^(k) + f (k=0,1,2,…), или в развернутом виде:

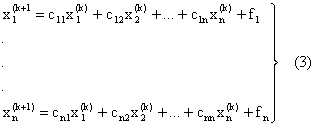
Производя итерации, получим последовательность векторов

х⁽¹⁾, х⁽²⁾,…, х^(k),…

Если элементы матрицы С удовлетворяют одному из условий

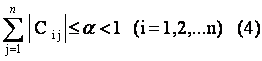или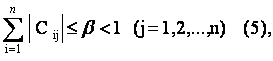

то процесс итерации сходится к точному решению системы Х при любом начальном векторе х⁽⁰⁾, т.е. .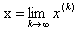

Таким образом, точное решение системы получается лишь в результате бесконечного процесса и всякий вектор х^(к) из полученной последовательности является приближенным решением. Оценка погрешности этого приближенного решения х^(к) дается одной из следующих формул:

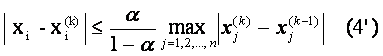
если выполнено условие (4)

или

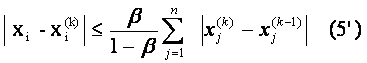
если выполнено условие (5).

Процесс итераций заканчивают, когда указанные оценки свидетельствуют о достижении заданной цели.

Начальный вектор х⁽⁰⁾ может быть выбран, вообще говоря, произвольно. Иногда берут х⁽⁰⁾=f. Однако наиболее целесообразно в качестве компонент вектора х⁽⁰⁾ взять приближенные значения неизвестных, полученные грубой прикидкой. Приведение системы (1) к виду (2) можно осуществить различными способами. Важно только, чтобы выполнялось одно из условий (4) или (5). Ограничимся рассмотрением двух способов.

Первый способ.

Если диагональные элементы матрицы А отличны от нуля, т.е. a_ij 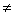0 (i=1,2,…,n), то систему (1) можно записать в виде

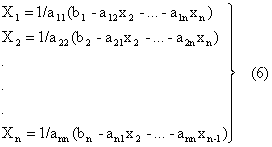
В этом случае элементы матрицы С определяются следующим образом:

С_ij= - a_ij/a_ii (i 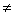j), c_ii=0, и тогда условия (4) и (5) приобретают вид

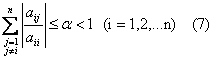
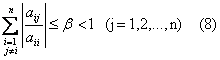
Неравенства (7), (8) будут выполнены, если диагональные коэффициенты для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).

Второй способ показан на примере (2).

Вообще говоря, для любой системы с невырожденной матрицей существуют сходящиеся итерационные методы решения, но далеко не всегда они удобны для практических вычислений.

Если метод итераций сходится, то:

1) Если итерации сходятся достаточно быстро, т. е. Если для решения системы требуется менее n итераций, то получаем выигрыш во времени, так как число арифметических действий, необходимых для одной итерации, пропорционально n² ,а общее число арифметических действий в методе Гаусса, например, пропорционально n³.

2) Погрешности округления в методе итераций сказываются значительно меньше, чем в методе Гаусса. Кроме того, метод итераций являетсясамоисчерпавляющимся, т.е. отдельная ошибка, допущенная в вычислениях, не отражается на окончательном результате, так как ошибочное приближение можно рассматривать как новый начальный вектор.

3) Метод итераций становится особенно выгодным при решении систем, у которых значительное число коэффициентов равно нулю. Такие системы появляются, например, при решении уравнений в частных производных.

4) Процесс итераций приводит к выполнению однообразных операций и сравнительно легко высчитывается на ЭВМ.

Пример 1.

Решить систему

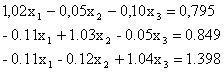
произведя три итерации. Указать погрешность результата.

Решение.

Матрица данной системы такова, что диагональные элементы близки к единице, а все остальные – значительно меньше единицы. Поэтому для применения метода итераций естественно записать систему в виде

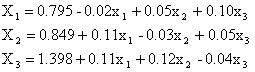
Условия сходимости для полученной системы выполнены

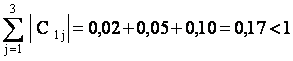
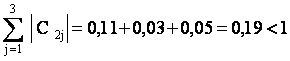
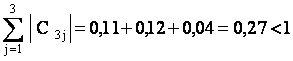
Берем в качестве начального вектора х⁽⁰⁾ столбец свободных членов, округлив его элементы до двух знаков после запятой:

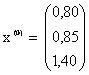
Далее последовательно находим при k = 1

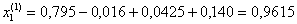
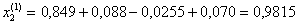
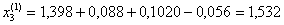
при k = 2

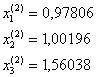
при k = 3

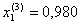
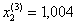
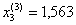
Значения неизвестных при k =2 и k = 3 отличны не более чем на 0,003, поэтому, если в качестве приближенных значений неизвестных взять 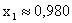, , 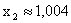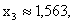то погрешность этих приближенных значений не превзойдет