Прямая и плоскость в пространстве
Матрицы
 Совокупность
Совокупность 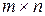 чисел, расположенный в виде прямоугольной таблицы из
чисел, расположенный в виде прямоугольной таблицы из 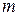 строк и
строк и 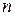 столбцов называется матрицейразмерности
столбцов называется матрицейразмерности 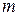 на
на 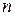 .
.
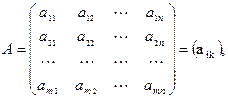
(1.1)
где 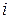 меняется от 1 до
меняется от 1 до 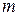 ,
, 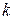 меняется от 1 до
меняется от 1 до 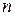
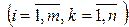 .
.
 Числа, составляющие матрицу, называются ее элементами:
Числа, составляющие матрицу, называются ее элементами: 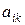 - элемент, находящийся в
- элемент, находящийся в 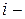 ой строке и
ой строке и 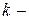 ом столбце.
ом столбце.
 Если
Если 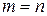 , то матрица называется квадратной порядка
, то матрица называется квадратной порядка 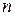 .
.
 Квадратная матрица, у которой равны нулю все элементы, не лежащие на главной диагонали
Квадратная матрица, у которой равны нулю все элементы, не лежащие на главной диагонали 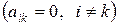 , называется диагональной.
, называется диагональной.
 Диагональная матрица, у которой все диагональные элементы равны 1 называется единичной:
Диагональная матрица, у которой все диагональные элементы равны 1 называется единичной:
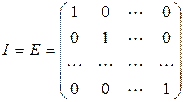 . (1.2)
. (1.2)
Одной из важнейших характеристик матрицы порядка 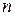 называется число - ее определитель, который обозначается
называется число - ее определитель, который обозначается 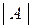 или
или 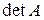 .
.
 Минором
Минором 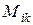 элемента
элемента 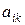 называется определитель, полученный из данного вычеркиванием
называется определитель, полученный из данного вычеркиванием 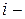 ой строки и
ой строки и 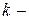 ого столбца, на пересечении которых находится элемент
ого столбца, на пересечении которых находится элемент 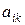 .
.
 Алгебраическим дополнением
Алгебраическим дополнением 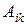 элемента
элемента 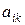 называется число, найденное по формуле
называется число, найденное по формуле
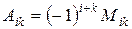 (1.3)
(1.3)
 Определителем
Определителем 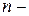 го порядка называется число, равное сумме произведений элементов любой строки (столбца) определителя на их алгебраические дополнения:
го порядка называется число, равное сумме произведений элементов любой строки (столбца) определителя на их алгебраические дополнения:
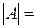
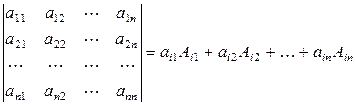 (1.4)
(1.4)
Таким образом,
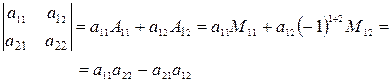
Итак, 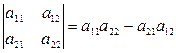 (1.5)
(1.5)
При вычислении определителей можно применять следующие их свойства.
1. 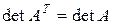 , где
, где 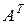 - транспонированная матрица (получена из данной матрицы заменой строк на столбцы с сохранением номеров элементов), т.е. строки и столбцы определителя равноправны.
- транспонированная матрица (получена из данной матрицы заменой строк на столбцы с сохранением номеров элементов), т.е. строки и столбцы определителя равноправны.
2. При перестановке двух соседних строк (столбцов) определитель меняет знак.
3. Если все элементы строки (столбца) равны нулю, то и определитель равен нулю.
4. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.
Определитель не изменится если его строку заменить линейной комбинацией этой и любой другой строк (суммой этой строки и любой другой, умноженной на одно и то же, не равное нулю число).
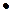 Две матрицы
Две матрицы 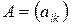 и
и 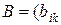 ) называются равными, если
) называются равными, если
они одной размерности и их соответствующие элементы равны, т.е. при всех 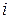 и
и 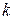
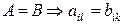 (1.6)
(1.6)
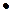 Суммой двух матриц одинаковой размерности А и В называется матрица С, каждый элемент которой равен сумме соответствующих элементов:
Суммой двух матриц одинаковой размерности А и В называется матрица С, каждый элемент которой равен сумме соответствующих элементов:
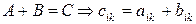 (1.7)
(1.7)
 Чтобы умножить матрицу А на число
Чтобы умножить матрицу А на число 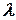 надо каждый элемент этой матрицы умножить на
надо каждый элемент этой матрицы умножить на 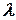 :
:
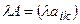 (1.8)
(1.8)
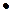 Если матрица А имеет размерность
Если матрица А имеет размерность 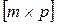 , а матрица В -
, а матрица В - 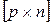 , то произведением матрицы А на В называется матрица С размерности
, то произведением матрицы А на В называется матрица С размерности 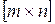 , элементы которой определяются равенствами:
, элементы которой определяются равенствами:
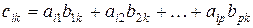 (1.9)
(1.9)
 Матрица
Матрица 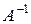 называется обратной по отношению к квадратной матрице А, если
называется обратной по отношению к квадратной матрице А, если
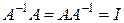 (1.10)
(1.10)
 Квадратная матрицу имеет обратную тогда и только тогда, когда ее определитель не равен 0.
Квадратная матрицу имеет обратную тогда и только тогда, когда ее определитель не равен 0.
 Для того, чтобы найти обратную матрицу надо:
Для того, чтобы найти обратную матрицу надо:
1. Вычислить ее определитель.
2. Заменить элементы матрицы их алгебраическими дополнениями и транспонировать полученную матрицу, которая называется присоединенной обозначим ее 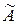 .
.
3. Разделить матрицу 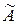 на определитель данной матрицы.
на определитель данной матрицы.
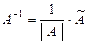 (1.11)
(1.11)
Система вида
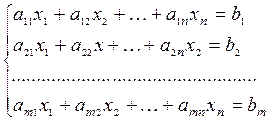 (1.12)
(1.12)
называется системой 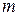 линейных уравнений с
линейных уравнений с 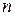 неизвестными. Эту систему можно записать в матричном виде:
неизвестными. Эту систему можно записать в матричном виде:
АХ = В, (1.12а)
Где 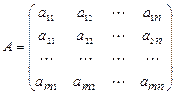 ,
, 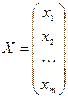 ,
, 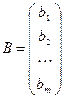 .
.
Одним из методов решения системы (1.12) является метода Гаусса. Для его применения надо:
1) расширенную матрицу 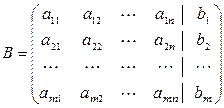
привести к треугольному виду, а именно
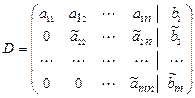
заменяя строки, начиная со второй линейной комбинацией этой строки и предыдущей.
2) По треугольной матрице 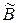 записать систему линейных уравнений (можно показать, что эта система будет эквивалентна данной системе) и решить ее «снизу вверх».
записать систему линейных уравнений (можно показать, что эта система будет эквивалентна данной системе) и решить ее «снизу вверх».
Векторы
1. Вектор – это направленный отрезок. Обозначаются векторы 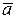 или или 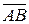 , где А – начало вектора, а В – его конец. Пусть , где А – начало вектора, а В – его конец. Пусть 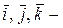 единичные, взаимно перпендикулярные векторы такие, что направление единичные, взаимно перпендикулярные векторы такие, что направление 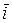 совпадает с направлением оси ОХ, совпадает с направлением оси ОХ, 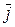 - оси ОУ, - оси ОУ, 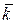 оси ОZ , тогда вектор оси ОZ , тогда вектор 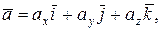 где где 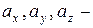 проекции вектора проекции вектора 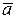 на соответствующие оси называются координатами этого вектора. на соответствующие оси называются координатами этого вектора. 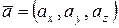 | ||
Пусть даны координаты точек А и В и векторов 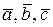 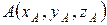 , , 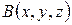 , , 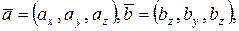 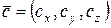 , тогда , тогда | ||
| 2. Координаты вектора по координатам начала и конца. | 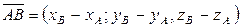 | |
| 3. Длина вектора | 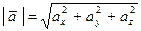 | |
4. Равные векторы, 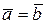 имеют равные координаты имеют равные координаты | 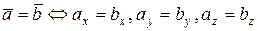 | |
| 5. Сумма (разность) векторов | 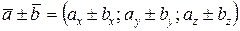 | |
6. Произведение вектора 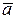 на скаляр (число) на скаляр (число) 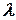 : : | 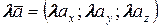 | |
7. Скалярным произведением вектора 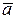 на вектор на вектор 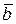 назы- вается число, равное произве-дению длин этих векторов на косинус угла между ними: назы- вается число, равное произве-дению длин этих векторов на косинус угла между ними: 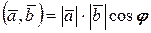 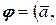 ^ ^ 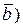 | 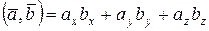 | |
| 8. Косинус угла между векто-рами равен скалярному про-изведению этих векторов на произведение их длин | 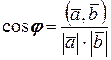 , , 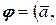 ^ ^ 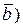 | |
9. Векторным произведением 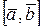 называется вектор называется вектор 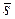 , такой что 1) , такой что 1) 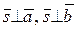 , , 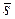 направлен так, что кратчайший поворот от направлен так, что кратчайший поворот от 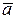 к к 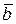 с конца с конца 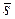 наблюдается против часовой стрелки; 2) наблюдается против часовой стрелки; 2) 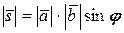 | 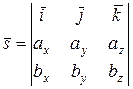 | |
10. Площадь параллелограмма, построенного на векторах 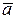 и и 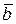 равна длине векторного про- изведения этих векторов. равна длине векторного про- изведения этих векторов. | 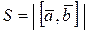 | |
11. Смешанное произведение трех векторов 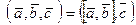 = = | 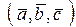 = = 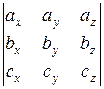 | |
12. Объем параллелепипеда, построенного на векторах 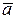 , , 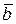 и и 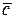 равен модулю их сме –шанного произведения равен модулю их сме –шанного произведения | 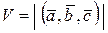 | |
| 13. Векторы называются компланарными, если они лежат или параллельны одной плоскости | 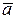 , , 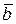 и и 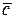 компланарны тогда и только тогда, когда компланарны тогда и только тогда, когда 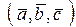 =0 =0 | |
| 14. Перпендикулярность (ортогональность) векторов | 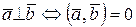 | |
| 15. Параллельность (коллинеарность) векторов | 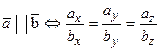 | |
16. Направляющие косинусы вектора 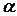 - угол между - угол между 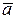 и положительным направлением оси ОХ, и положительным направлением оси ОХ, 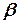 - между - между 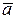 и положительным направлением оси ОY, и положительным направлением оси ОY, 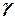 - между - между 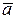 и положительным направлением оси OZ и положительным направлением оси OZ | 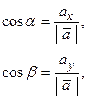 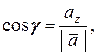 | |
17. Орт вектора 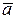 ( ( 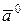 )- единичный вектор того же направления, что и вектор )- единичный вектор того же направления, что и вектор 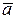 | 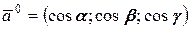 | |
| 18. Координаты точки С – середины отрезкаАВ | 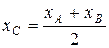 , , 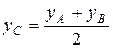 , , 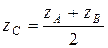 | |
Прямая и плоскость в пространстве
1.Уравнение плоскости, проходя-щей через точку 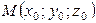 перпендикулярно вектору перпендикулярно вектору 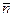 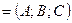 , , 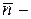 нормальный вектор нормальный вектор | 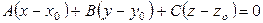 |
2.Общее уравнение плоскости 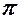 | 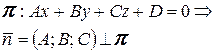 |
Пусть 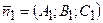 - нормальный вектор плоскости - нормальный вектор плоскости 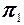 , а , а 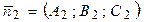 - нормальный вектор плоскости - нормальный вектор плоскости 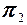 , тогда имеют место соотношения , тогда имеют место соотношения | |
| 3. Перпендикулярность плоскостей | 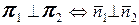 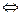 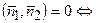 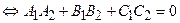 |
| 4. Параллельность плоскостей | 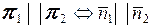 |
5. Угол между плоскостями 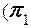 ^ ^ 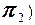 | 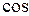 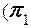 ^ ^ 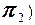 = = 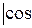 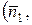 ^ ^ 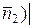 |
6. Расстояние от точки 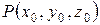 до плоскости до плоскости 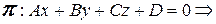 | 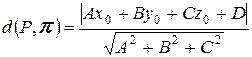 |
Пусть прямая 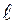 проходит через точку проходит через точку 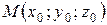 параллельно век-тору параллельно век-тору 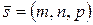 , ( , ( 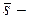 направляющий вектор прямой направляющий вектор прямой 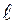 ), тогда ), тогда  | |
7. Канонические уравнения прямой 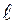 | 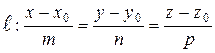 |
8. Параметрические уравнения прямой 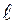 | 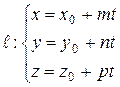 |
Пусть 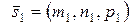 - направляющий вектор прямой - направляющий вектор прямой 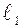 , а , а 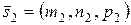 - прямой - прямой 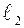 , тогда имеют место соотношения: , тогда имеют место соотношения: | |
| 9. Параллельность прямых | 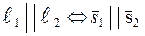 |
| 10. Перпендикулярность пря-мых | 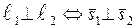 |
| 11. Угол между прямыми | 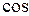 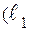 ^ ^ 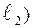 = = 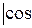 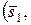 ^ ^ 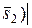 |
