Метод Драгилева А. В. (решение систем нелинейных уравнений)
Метод Драгилева развивает идею метода продолжения по параметру. Продолжение по параметру предполагает использование в качестве независимой переменной параметр, искусственно введённый в систему или назначенный из числа переменных, находящихся в системе изначально. Возьмём за основу один из самых простых вариантов метода продолжения по параметру. Пусть (1) система уравнений относительно Y:
 |
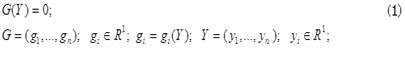
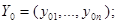Выберем точку
 |
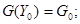Значение, которое в этой точке примет система (1), будет
И рассмотрим новую систему уравнений:
В этой системе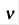 
– параметр, который в случае 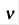= 0 обращает (1a) в (1), а в случае, когда 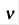равен 1, то в точке
| |
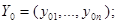левая часть (1а) обращается в 0. Таким образом, если в (1а) предположить, что:
 |
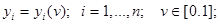Изменяя параметр от 1 до 0, можно от решения (1а) прийти к решению (1). Участок кривой, который описывает при этом (1а), должен соответствовать монотонному изменению всех координат. Это более слабое условие, чем для метода Ньютона, но если речь идёт о поиске решения почти “вслепую”, метод продолжения по параметру имеет мало преимуществ перед методами типа метода Ньютона.
Если в (1а) 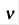рассматривать в качестве n+1 координаты, то (1а) станет системой n уравнений относительно n+1 переменной. И когда значение n+1-я переменная будет принимать значение 0, то остальные переменные будут доставлять решение исходной системе уравнений. Начальное значение для 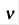1, а значения остальных координат выбираются как начальная точка для нахождения решения системы нелинейных уравнений (1).
Рассмотрим систему из n уравнений, в которой количество переменных равно n+1. Такая система описывает некую кривую в пространстве размерности n+1:
 |
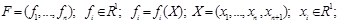Строим кривую (2), приняв в качестве независимой переменной длину дуги самой кривой. Координаты точек кривой получаем как решение задачи Коши для системы обыкновенных дифференциальных уравнений, начальными данными для которой будут координаты заранее известной точки, принадлежащей этой кривой.
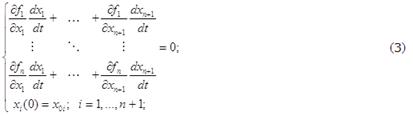
(3) - это однородная система линейных уравнений n относительно n+1 производных от искомых координат. Решаем систему с помощью правила Крамера. За свободную переменную можно принять любую производную, например, n+1 производную. Присвоим ей значение главного определителя системы, чтобы избавиться от знаменателей. И вместо (3) получаем следующую систему уравнений:
Длина дуги не зависит от выбора параметра t, и она возрастает вместе с t. Значение t=0 соответствует выбранной начальной точке, от которой кривая будет строиться в обоих направлениях, в “положительном” направлении шаг интегрирования будет положительным, а в “отрицательном” – отрицательным. Для решения (3а) можем применить стандартный алгоритм численного решения задачи Коши, чтобы построить кривую (2).
В процессе построения кривой 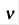может менять знак, это будет означать, что кривая пересекает пространство размерности n, и в этом месте будет область, содержащая решение (1). Количество найденных решений будет соответствовать числу перемен знака параметра. Кривая может проходить точки экстремумов. Это позволяет находить решения весьма удалённые от начальной точки и находить более одного решения для одной начальной точки. Можно сказать, метод имеет слабую зависимость от начального приближения.
---------------------------------------------------------------------------------------------
Этот метод был разработан в 1979 году КФМН Драгилевым Анатолием Владимировичем (1923 –1997) г.
---------------------------------------------------------------------------------------------