Проходящей через три заданные точки

Пусть М₁(x₁, y₁ ,z₁), М₂(x₂, y₂ ,z₂), М₃(x₃, y₃ ,z₃) - три заданные точки и М(x, y ,z) – произвольная точка плоскости.

Тогда векторы 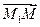, , 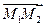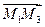лежат в одной плоскости, т.е. компланарны. Условием компланарности трех векторов является равенство нулю определителя третьего порядка, составленного из координат этих векторов,

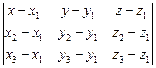= 0.

(3.4)

Это – уравнение плоскости, проходящей через три заданные точки.

Если плоскость пересекает оси координат в точках М₁(а, 0 , 0), М₂(0, b, 0), М₃(0, 0 , c), то уравнение (3.4) примет вид

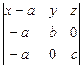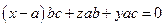= 0 Þ Þ =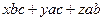

= .

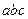Деля последнее уравнение на 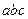, получим уравнение

.

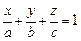(3.5)

В этом уравнении a, b, c – отрезки, отсекаемые плоскостью на осях координат 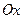, , 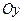,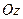соответственно, поэтому оно называется уравнением плоскости в отрезках.

Пример 3.2

Составить уравнение плоскости, проходящей через три заданные точки: М₁(2, –1 , 3), М₂(–1, 1 , 4), М₃(–2, 5 , 2).

Решение

Подставив координаты точек в уравнение (3.4), получим

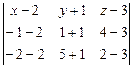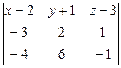= 0 Þ = 0,

Раскладывая определитель по элементам первой строки, получим

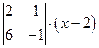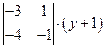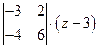– + = 0, Þ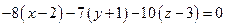

Þ , Þ 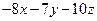+16–7+30= = 0, Þ 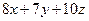– 39 = 0.

Угол между двумя плоскостями

Рассмотрим задачу о вычислении угла между двумя плоскостям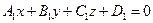и и .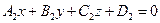

Угол между плоскостями измеряется линейным углом, который равен углу между нормальными векторами 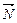₁(A₁, B₁, C₁) и 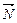₂(A₂, B₂, C₂) этих плоскостей. Поэтому

.

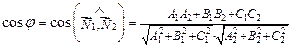(3.6)

Если плоскости ортогональны, то ортогональны (взаимно перпендикулярны) и их нормальные векторы. В этом случае 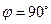, , 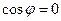тогда из формулы (3.6) следует условие ортогональности плоскостей

.

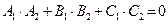(3.7)

Если плоскости параллельны, то параллельны и их нормальные векторы. Координаты параллельных векторов пропорциональны:

.

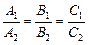(3.8)

Уравнения (3.8) представляют собой условия параллельности плоскостей.

Общие уравнения прямой

Прямую линию в пространстве можно рассматривать как линию пересечения двух плоскосте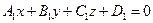й и 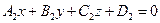, т.е. как множество точек, координаты которых удовлетворяют системе уравнений

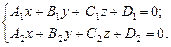
Эти уравнения называются общими уравнениями прямой.

Канонические уравнения прямой

Прямая в пространстве определяется однозначно, если известна точка М₀(х₀, y₀, z₀), через которую проходит эта прямая, и вектор 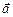(m, n, p), параллельный этой прямой. Такой вектор называют направляющим вектором прямой.

z

M0

M1

M

O

y

х

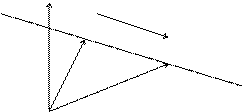
Рис. 3.2

Составим уравнение прямой, проходящей через точку М₀, параллельно вектору 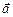(рис.3.2). Пусть 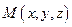– произвольная точка, лежащая на прямой L, тогда вектор

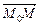= (x – x₀, y – y₀, z – z₀) коллинеарен вектору 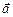(m, n, p). Условием коллинеарности векторов является пропорциональность координат, поэтому получаем уравнения

,

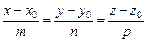(3.9)

Эти уравнения называются каноническими уравнениями прямой.

Пример 3.3

Составить канонические уравнения прямой, проходящей через точку М₀(1,–2, 3) параллельно вектору 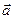= (2, 0, –3).

Решение

Подставим координаты точки М₀ и координаты вектора 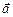в уравнение (3.9), получим

.

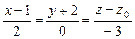Уравнения прямой,