Прямоугольная система координат
Аналитическое описание векторов и точек пространства осуществляется при помощи чисел.
Введем в пространстве прямоугольную декартову систему координат x, y, z, т.е. три взаимно перпендикулярные прямые (оси), проходящие через точку О, называемую началом. Прямые направлены и называются осями координат x, y, z. Предполагается, что выбрана единица масштаба.
Направление осей координат зададим единичными векторами (ортами) 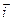 ,
, 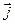 ,
, 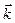 .
.
Возьмем произвольную точку М. Вектор  называется радиус-вектором точки М:
называется радиус-вектором точки М:  . Радиус-вектор, в свою очередь, определяет некоторый вектор
. Радиус-вектор, в свою очередь, определяет некоторый вектор  , который можно переносить в пространстве параллельно самому себе. Найдем проекции вектора
, который можно переносить в пространстве параллельно самому себе. Найдем проекции вектора  на оси координат: очевидно, что
на оси координат: очевидно, что


Такая картинка называется разложением вектора  по трем координатным осям. Проекции радиус вектора
по трем координатным осям. Проекции радиус вектора  на координатные оси обозначим через x, y, z.
на координатные оси обозначим через x, y, z.
Координатами точки М в пространстве называются проекции вектора  на соответствующие координатные оси: M (x, y, z).
на соответствующие координатные оси: M (x, y, z).
 (*) или
(*) или  .
.
Проекции вектора на координатные оси называются координатами вектора.
Равенство (*) – основное равенство векторной алгебры. Его называют разложением вектора  по координатным осям (по базису
по координатным осям (по базису 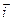 ,
, 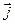 ,
, 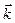 ).
).
Действия над векторами в проекциях.
Пусть даны два радиус-вектора в разложении по координатным осям:
 или
или 
 или
или 
1. два радиус-вектора равны  тогда и только тогда, когда равны их проекции:
тогда и только тогда, когда равны их проекции:

2. Чтобы умножить радиус-вектор на число, надо каждую из его проекций умножить на это число:
 или
или  .
.
3. Чтобы сложить (вычесть) два радиус-вектора, надо сложить (вычесть) их одноименные координаты.
 или
или  .
.
Координаты вектора 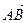 .
.

Пусть даны координаты точек  и
и  . Найдем координаты вектора
. Найдем координаты вектора  . Рассмотрим радиус-векторы:
. Рассмотрим радиус-векторы:  и
и  .
.
Очевидно, что  . В координатной форме:
. В координатной форме:  .
.
Чтобы найти координаты вектора  , нужно из координат его конца вычесть координаты начала.
, нужно из координат его конца вычесть координаты начала.
Обозначим:  . Тогда
. Тогда  или
или  .
.
Т.к. произвольный вектор всегда можно сделать радиус-вектором, то свойства действий 1, 2, 3 остаются в силе.
Условие коллинеарности векторов в координатной форме.
Пусть  и
и  - коллинеарные векторы.
- коллинеарные векторы.
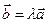 (*).
(*).
Если векторы коллинеарны, то их координаты пропорциональны:

Пример 1.  ,
,  .
.
Пример 2.  . Коллинеарны ли векторы
. Коллинеарны ли векторы  и
и  ?
?

Скалярное произведение векторов.
Скалярным произведением двух векторов  и
и 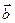 называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними.
 или
или  (1)
(1)
 Физический смысл. Работа при прямолинейном перемещении материальной точки на расстояние S=|MN| под действием постоянной силы F вычисляется по формуле:
Физический смысл. Работа при прямолинейном перемещении материальной точки на расстояние S=|MN| под действием постоянной силы F вычисляется по формуле:  . Если ввести вектор перемещения
. Если ввести вектор перемещения  , то можно записать эту формулу в виде:
, то можно записать эту формулу в виде:
 .
.
