Линейные операции над векторами
Векторы
1 На плоскости даны два вектора 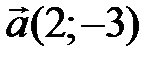 и
и 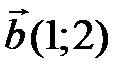 . Найдите разложение вектора
. Найдите разложение вектора 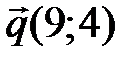 по базису
по базису 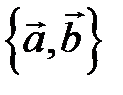 .
.
2 Даны три последовательные вершины параллелограмма 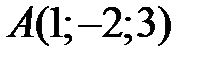 ,
, 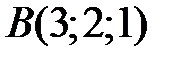 ,
, 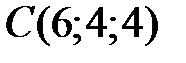 . Найдите его четвертую вершину
. Найдите его четвертую вершину 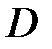 .
.
3 Даны вершины четырехугольника 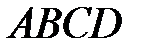 :
: 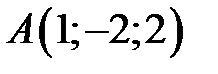 ,
, 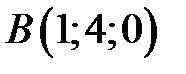 ,
, 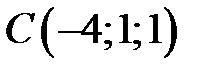 ,
, 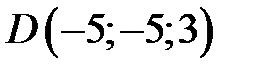 . Докажите, что его диагонали взаимно– перпендикулярны.
. Докажите, что его диагонали взаимно– перпендикулярны.
4 В четырехугольнике 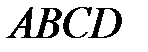
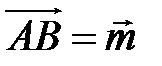 ,
, 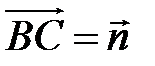 ,
, 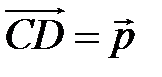 . Найдите разложение вектора
. Найдите разложение вектора 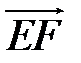 , где
, где 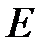 и
и 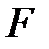 ― середины диагоналей
― середины диагоналей 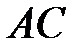 и
и 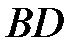 по векторам
по векторам 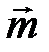 ,
, 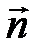 ,
, 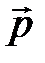 .
.
5 Дан правильный шестиугольник 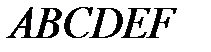 . Найдите разложение векторов
. Найдите разложение векторов 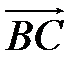 ,
, 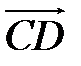 ,
, 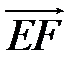 ,
, 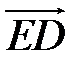 по векторам
по векторам 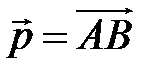 ,
, 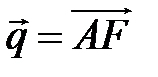 .
.
6 Дана трапеция 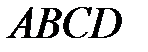 , у которой основание
, у которой основание 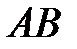 в два раза больше основания
в два раза больше основания 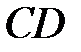 . Точки
. Точки 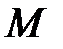 и
и 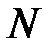 ― середины оснований. Найдите разложение векторов
― середины оснований. Найдите разложение векторов 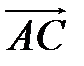 ,
, 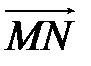 и
и 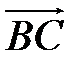 по векторам
по векторам 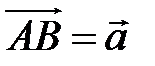 ,
, 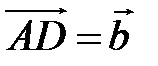 .
.
7 В треугольнике 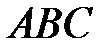 проведены медианы
проведены медианы 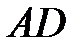 ,
, 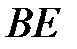 ,
, 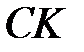 . Докажите, что
. Докажите, что 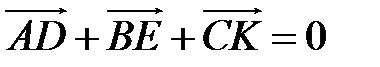 .
.
8 Точка  ― центр правильного шестиугольника
― центр правильного шестиугольника 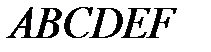 . Найдите разложение векторов
. Найдите разложение векторов 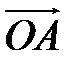 ,
, 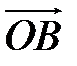 ,
, 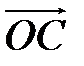 ,
, 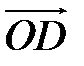 по векторам
по векторам 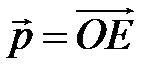 ,
, 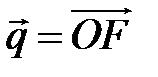 .
.
9 Дан параллелепипед 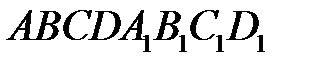 , в котором
, в котором 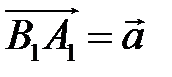 ,
, 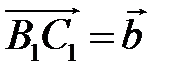 ,
, 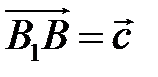 . Разложите вектор
. Разложите вектор 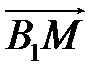 по векторам
по векторам 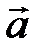 ,
, 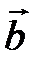 и
и 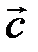 , где
, где 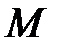 ― точка пересечения
― точка пересечения 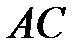 и
и 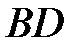 .
.
10 Дан параллелограмм 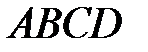 ,
, 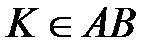 ,
, 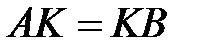 ,
, 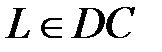 ,
, 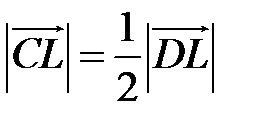 . Выразите вектор
. Выразите вектор 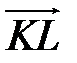 через векторы
через векторы 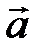 и
и 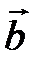 , если
, если 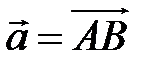 ,
, 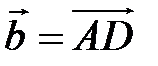 .
.
11 Дан параллелограмм 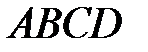 ,
, 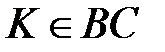 ,
, 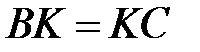 ,
, 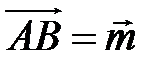 ,
, 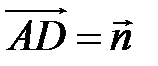 . Выразите вектор
. Выразите вектор 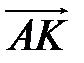 через векторы
через векторы 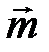 и
и 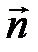 .
.
12 Дан параллелограмм 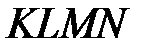 ,
, 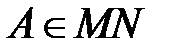 ,
, 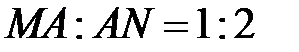 ,
, 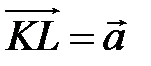 ,
, 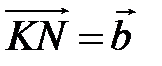 . Выразите вектор
. Выразите вектор 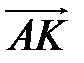 через векторы
через векторы 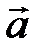 и
и 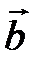 .
.
13 Даны три вектора 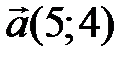 ,
, 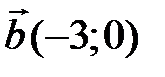 ,
, 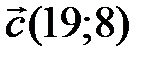 . Найдите разложение векто-ра
. Найдите разложение векто-ра 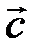 по векторам
по векторам 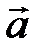 и
и 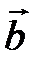 . Чему равны координаты вектора
. Чему равны координаты вектора 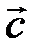 в базисе
в базисе 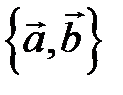 ?
?
14 Найдите разложение вектора 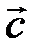 по векторам
по векторам 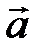 и
и 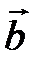 , если
, если 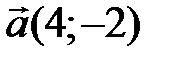 ,
, 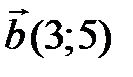 и
и 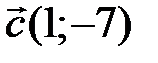 . Чему равны координаты вектора
. Чему равны координаты вектора 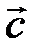 в базисе
в базисе 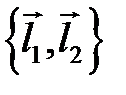 , если
, если 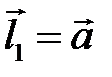 ,
, 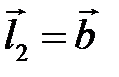 ?
?
15 В ромбе 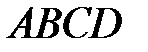 за базисные взяты векторы
за базисные взяты векторы 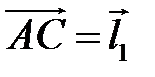 и
и 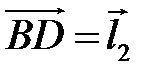 . Найдите координаты векторов
. Найдите координаты векторов 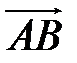 ,
, 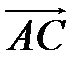 ,
, 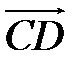 ,
, 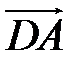 в этом базисе.
в этом базисе.
16 На трех некомпланарных векторах 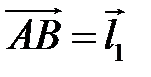 ,
, 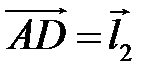 и
и 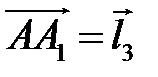 построен параллелепипед
построен параллелепипед 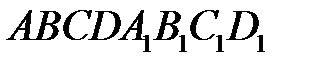 . Найдите координаты векторов
. Найдите координаты векторов 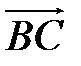 ,
, 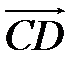 ,
, 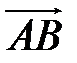 ,
, 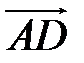 ,
, 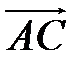 ,
, 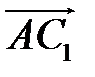 ,
, 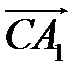 ,
, 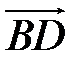 ,
, 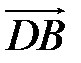 в базисе
в базисе 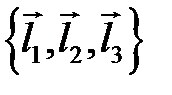 .
.
17 В правильном шестиугольнике 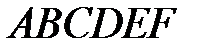 векторы
векторы 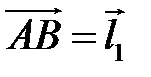 и
и 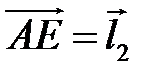 выбраны в качестве базисных. Найдите в этом базисе координаты векторов
выбраны в качестве базисных. Найдите в этом базисе координаты векторов 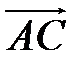 ,
, 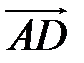 ,
, 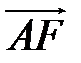 ,
, 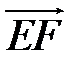 .
.
18 Пусть 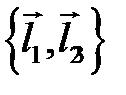 ― произвольный базис на плоскости. Диагонали параллелограмма построены на векторах
― произвольный базис на плоскости. Диагонали параллелограмма построены на векторах 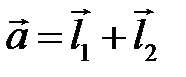 и
и 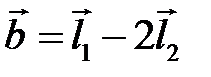 . Найдите координаты этих диагоналей.
. Найдите координаты этих диагоналей.
19 Проверьте, что четыре точки 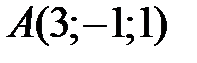 ,
, 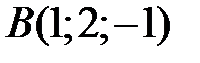 ,
, 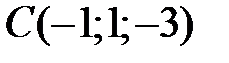 ,
, 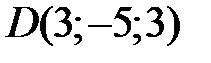 служат вершинами трапеции.
служат вершинами трапеции.
20 Дан тетраэдр 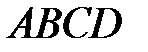 .
. 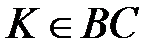 ,
, 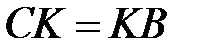 ,
, 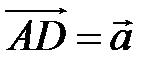 ,
, 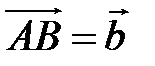 ,
, 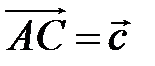 . Выразите вектор
. Выразите вектор 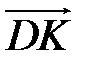 через векторы
через векторы 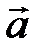 ,
, 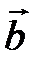 ,
, 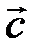 .
.
21 На плоскости даны два вектора 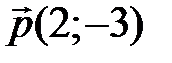 и
и 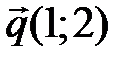 . Найдите разложение вектора
. Найдите разложение вектора 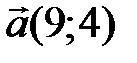 по базису
по базису 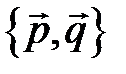 .
.
22 Даны точки 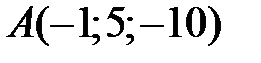 ,
, 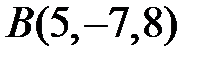 ,
, 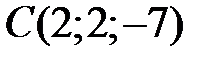 ,
, 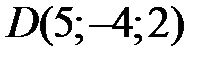 . Проверьте, что векторы
. Проверьте, что векторы 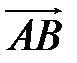 и
и 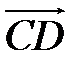 коллинеарны; установите, длина которого из них больше и во сколько раз, как они направлены – противоположно или сонаправленно?
коллинеарны; установите, длина которого из них больше и во сколько раз, как они направлены – противоположно или сонаправленно?
23 Даны три вектора 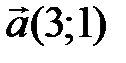 ,
, 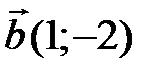 ,
, 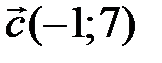 . Определите разложение вектора
. Определите разложение вектора 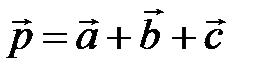 по базису
по базису 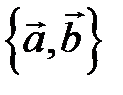 .
.
24 На плоскости даны четыре точки 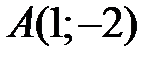 ,
, 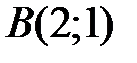 ,
, 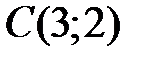 ,
, 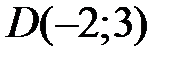 . Определите разложение векторов
. Определите разложение векторов 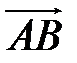 ,
, 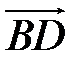 ,
, 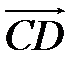 и
и 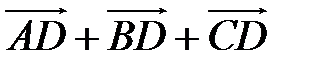 , принимая в качестве базисных
, принимая в качестве базисных 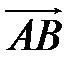 и
и 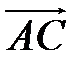 .
.
25 В ромбе 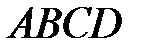 даны диагонали
даны диагонали 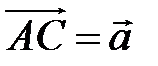 ,
, 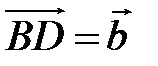 . Разложите по этим двум векторам все векторы, которые совпадают с медианами
. Разложите по этим двум векторам все векторы, которые совпадают с медианами 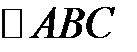 .
.
26 Даны три вектора 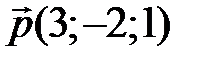 ,
, 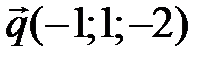 ,
, 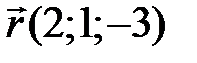 . Найдите разложение вектора
. Найдите разложение вектора 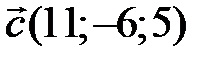 по базису
по базису 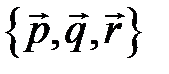 .
.
27 Векторы 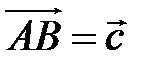 ,
, 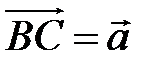 ,
, 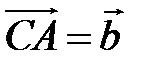 образуют треугольник
образуют треугольник 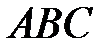 . Выразите через векторы
. Выразите через векторы 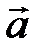 ,
, 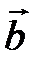 ,
, 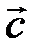 векторы
векторы 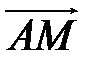 ,
, 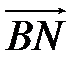 ,
, 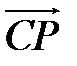 , которые совпадают с медианами треугольника
, которые совпадают с медианами треугольника 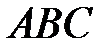 .
.
28 Проверьте, является ли четырехугольник с вершинами в точках 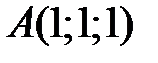 ,
, 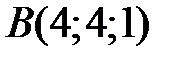 ,
, 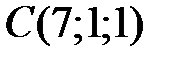 ,
, 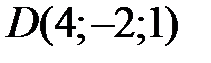 квадратом.
квадратом.
29 Дан треугольник с вершинами 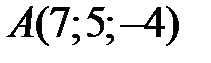 ,
, 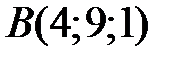 ,
, 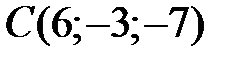 . Вычислите длину медианы, проведенной из вершины
. Вычислите длину медианы, проведенной из вершины 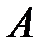 , и периметр
, и периметр 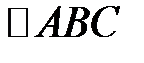 .
.
30 Найдите длины диагоналей параллелограмма, построенного на векторах 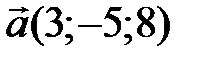 ,
, 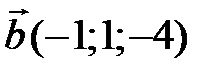 .
.
