Согласование длинной линии и нагрузки

Расчет переходной проводимости ЛРП, обеспечивающей формирование заданного прямоугольного импульса, основывается на заданном значении сопротивления нагрузки R, причем обеспечивается условие R = r [3], [4]. Параметры ЛПР определяются по (3.1) и (3.2).

Поскольку на практике отношение сопротивлений a = R/r, называемое коэффициентом согласования, строго говоря, никогда не равно единице, необходимо оценить величину допустимых отклонений значений a, не нарушающих существенно процесс формирования импульсов. Обратимся вновь к схеме формирования импульсов на рис. 2.13. Учитывая, что r = R, запишем (2.6) в виде

.

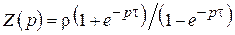Преобразованная функция I(p) для тока нагрузки i(t)будет следующий:

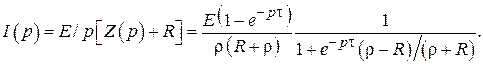(3.3)

Следуя примененному в 2.1 приему и разлагая в бесконечный ряд последнюю дробь выражения (3.3), получим

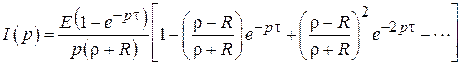. (3.4)

Величину

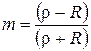(3.5)

называют коэффициентом отражения. Найдем связь между коэффициентами согласования a и отражения m.

Разделим числитель и знаменатель выражения (3.5) на r. Получим . Решив это уравнение относительно a, найдем, что a =
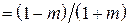. Таким образом, в случае согласованной нагрузки a = 1 и m = 0.

При R > r коэффициент согласования a > 1, а коэффициент отражения m < 0; при R < r коэффициент согласования 1 > a > 0, а m >0. Если ввести в зависимость (3.4) коэффициент m, то получим

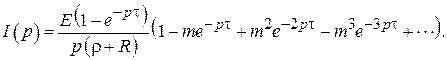(3.6)

Зависимости (3.4) и (3.6) подобны рассмотренному выражению (2.5). Аналогично предыдущему, учитывая, что 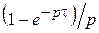есть преобразованная функция прямоугольного импульса длительностью t с амплитудой, равной единице, и, применяя теорему запаздывания, находим почленно исходную функцию тока i(t). Ток будет представлять собой сумму прямоугольных импульсов длительностью t, возникающих последовательно в момент времени t = 0, t, 2t, 3t... и, соответственно, обладающих амплитудами I1 = E/(r + R); I2 = I1|m|; I3 = I1m2; ...; In = I1|m|(n – 1).

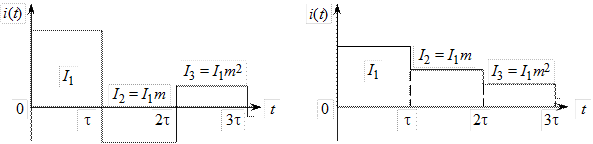
Рис. 3.3 Рис. 3.4

При a < 1 m > 0 и, следовательно, полярность импульсов поочередно изменяется. При a > 1 m < 0 и все импульсы имеют одинаковую полярность. На рис. 3.3 и 3.4 графически представлены токи нагрузки для значений m = +0,5 и m = –0,5, т. е. для значений a = 1/3 и a = 3. В промежуточном случае при a = 1 и m = 0 основной импульс тока является единственным.

Значения напряжений на нагрузке и токи в цепи, действующие тотчас по окончании основного импульса, отнесенные к амплитуде основного импульса, равны абсолютному значению коэффициента отражения U2/U1 = I2/I1 = |m|.

Отсюда по заданному допустимому значению U2/U1можно найти область допустимых значений a. Если m £ 0,1, то для m = 0,1 a1 = 0,82, а для m = –0,1 a2 = 1,22. Таким образом, сопротивление нагрузки R должно лежать в пределах: 0,82r < R < 1,22r.

При изменении a изменяется также энергия импульса в нагрузке, равная Wн = E2Rt/(r + R)2. Эта величина имеет максимальное значение при R = r, равное

Wнmax = E2t/4r.

Обозначим относительное уменьшение энергии импульса по сравнению с ее максимальным значением:

D = 1 – Wн/Wнmax.

Тогда

D = 1 – 4Rr/(R + r)2 = 1 – 4a/(1 + a)2.

Отсюда

a2– 2a(1 + D)/(1 – D) + 1 = 0,1.

Соответственно,

a = (1 + D ± 2 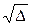)/(1 – D).

Задаваясь D = 0,05, получим a1 = 1,56 и a2 = 0,64. Следовательно, чтобы уменьшение энергии импульса по отношению к максимальному значению не превышало 5 %, необходимо ограничить значения сопротивления нагрузки в пределах 0,64r < R < 1,56r. Таким образом, даже резкая несогласованность сопротивлений влияет на значение энергии основного импульса незначительно, что положительно проявляется на практике. Это свойство генераторов импульсов позволяет обеспечить стабильную работу импульсных электротехнологических установок, нагрузки которых в большинст­ве случаев либо являются нелинейными, либо изменяются во времени.