Форма и параметры импульсов
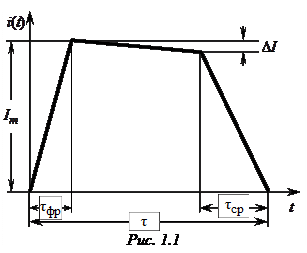В импульсной технике применяются импульсы токов или напряжений самых различных форм. Основными идеализированными формами являются прямоугольные, трапецеидальные, треугольные, экспоненциальные и колокольные. При этом различают такие участки импульсов, как фронт, вершина, срез, основание и хвост. Основные параметры импульсов следующие (рис. 1.1): 
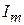– амплитуда импульса; DI – спад вершины импульса; t – длительность импульса; 
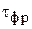– длительность фронта; 
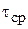– длительность среза. Измерение длительностей как самих импульсов, так и их отдельных участков становится малоопределенным при работе с реальными импульсами, не имеющими простой геометрической формы (рис. 1.2). Поскольку определение временных параметров импульсов такой формы затруднительно, для характеристики формы реальных импульсов введено понятие об активных длительностях, определяющихся разностями соответствующих моментов времени, в которые импульс i(t) принимает значения 
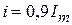и 
.
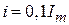Тогда временные параметры импульсов можно определить как междецильные интервалы:
; 
; 
.
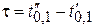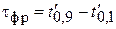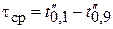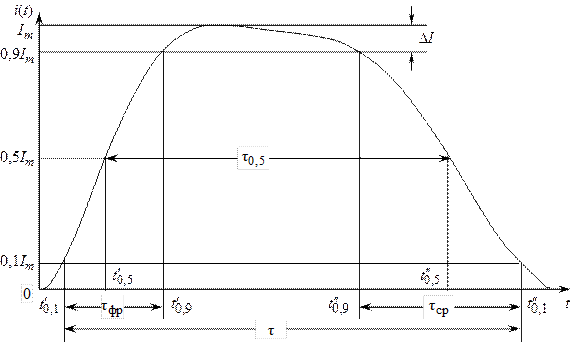
Рис. 1.2
Для импульсов, не имеющих явно выраженных фронта, среза и плоской части, вводится понятие длительности импульса на уровне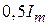 
, т. е. 
.
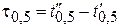Прямоугольные импульсы, получаемые с помощью ФД или ОИЛ, имеют на своей вершине колебания, которые называются осцилляциями и чаще всего являются нежелательными. Неравномерность вершины определяется значением выброса импульса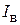 
, который, в свою очередь, определяет пиковое значение импульса 
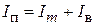. При этом высота импульса 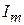, выражающая его номинальное значение, обычно определяется без учета осцилляций [4].
Средним значением последовательности импульсов, определяющим постоянную составляющую импульсного процесса, называется величина
.
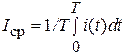Для последовательности прямоугольных импульсов тока с амплитудой Im
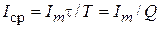. (1.1)
Действующее значение последовательности импульсов тока произвольной формы
.
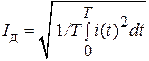Для последовательности прямоугольных импульсов тока с амплитудой Im
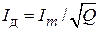. (1.2)
Из сопоставления формул (1.1) и (1.2) следует, что действующее значение параметров импульсного процесса больше его среднего значения в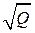 
раз.
При генерировании в нагрузке импульсов произвольной формы среднее значение тока за время длительности импульса t
,
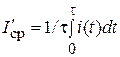а действующее значение
.
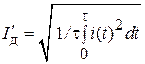На отрезке времени 0…t среднее и действующее значения импульсов произвольной формы могут быть представлены эквивалентными прямоугольными импульсами с амплитудам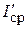и 
и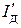 
. Тогда среднее и действующее значения тока нагрузки за период равны, соответственно,
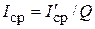и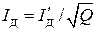 
.
В тех случаях, когда в нагрузке генерируются импульсы полусинусоидальной формы, среднее и действующее значения тока за время t равны, соответственно,
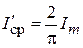, а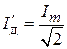 
.
Токи нагрузки за период частоты следования импульсов:
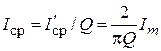, (1.3)
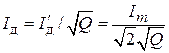. (1.4)
Отношение среднего и действующего значений тока
.
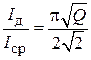В ряде случаев, когда форма импульсов не является определяющей для электрофизического процесса, достаточно использовать полный разряд емкостного накопителя величиной C, заряжаемого до максимального напряжения Umв паузу между импульсами. В резистивной нагрузке R будут генерироваться импульсы экспоненциальной формы, длительность которых теоретически равна бесконечности. Примем во внимание, что за время t ³ 5RC практически вся энергия, запасенная в емкостном накопителе, реализуется в нагрузке, а длительность периода T >> 5RC . Тогда среднее значение тока нагрузки
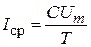. (1.5)
Действующее значение тока нагрузки Iдможно найти следующим образом. Средняя мощность, выделяемая в резистивной нагрузке,
.
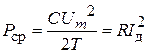Отсюда
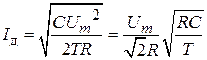. (1.6)
Введем понятие скважности для этого случая как
.
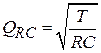Тогда зависимость (1.4) примет вид
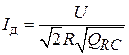
и из сопоставления (1.5) и (1.6) отношение действующего и среднего значений токов
.
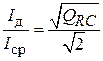Следует отметить, что на практике достаточно часто в цепь разряда емкостного накопителя включается дополнительная индуктивность L для ограничения скорости нарастания тока силового коммутатора. При этом форма импульса отличается от экспоненциальной, а фронт импульса приобретает конечную длительность, отличную от нуля. Если выдерживается соотношение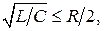 
т. е. процесс разряда емкостного накопителя является апериодическим или критическим и происходит за отрезок времени, существенно меньший, чем длительность периода, то зависимости (1.5) и (1.6) остаются справедливыми. В тех случаях, когда 
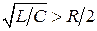, процесс разряда емкостного накопителя будет колебательным. При наличии коммутатора, обладающего вентильными свойствами, импульс тока нагрузки будет иметь форму, близкую к полусинусоидальной, и тогда для определения приближенных значений среднего и действующего токов могут быть использованы зависимости (1.3) и (1.4).