Точка пересечения прямой и плоскости

Дана прямая: 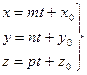(1) и плоскость: Ax + By + Cz + D = 0 (2).

Найдем координаты точки пересечения прямой и плоскости. Если прямая (1) и плоскость (2) пересекаются, то координаты точки пересечения удовлетворяют уравнениям (1) и (2):

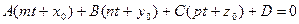отсюда

, .

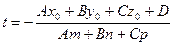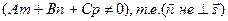Подставляя найденное значение t в (1), получим координаты точки пересечения.

1) Если Am + Bn + Cp = 0, а Ax₀ + By₀ + Cz₀ + D ≠ 0, то 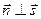и t не существует, т.е. прямая и плоскость не имеют ни одной общей точки. Они параллельны.

2) Am + Bn + Cp = 0 и Ax₀ + By₀ + Cz₀ + D = 0. В этом случае t может принимать любые значения и 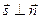, т.е. прямая параллельна плоскости и имеет с ней общую точку, т.е. она лежит в плоскости.

Пример 1. Найти точку пересечения прямой 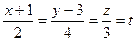с плоскостью 3x – 3y + 2z – 5 = 0.

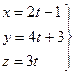, 3(2t – 1) – 3(4t + 3) + 2·3t – 5 = 0 => -17=0, что невозможно ни при одном t, т.е. прямая и плоскость не пересекаются.

Пример 2. Найти точку пересечения прямой 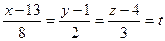и плоскости: x + 2y – 4z + 1 = 0.

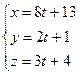, 8t + 13 + 2(2t + 1) – 4(3t + 4) + 1 = 0, 0 + 0 = 0. Это верно при любом значении t, т.е. прямая лежит в плоскости.

Пример 3. Найти точку пересечения прямой 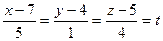и плоскости 3x – y + 2z – 5 = 0.

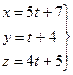, 3(5t + 7) – t – 4 + 2(4t + 5) – 5 = 0, 22t + 22 = 0, t = -1, x = 5(-1) + 7 = 2, y = -1 + 4 = 3, z = 4(-1) + 5 = 1, M(2, 3, 1) – точка пересечения прямой и плоскости.

Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.

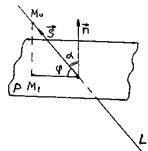Углом между прямой и плоскостью называется острый угол ц между прямой и ее проекцией на плоскость.

Пусть заданы прямая и плоскость:

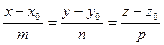и .

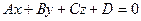Пусть прямая пересекает плоскость и образует с ней угол ц ( ). Тогда б = 90⁰ – ц или б = 90⁰ + ц – это угол между нормальным вектором плоскости и направляющим вектором прямой 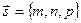. Но 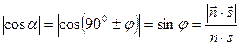. Значит

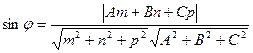(3).

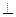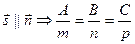а) Если L P, то - условие перпендикулярности прямой и плоскости.

б) Если L||P, то 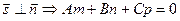- условие параллельности прямой и плоскости.

в) Если прямая L||P и при этом точка M0(x0, y0, z0) 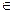P, то прямая лежит в данной плоскости. Аналитически:

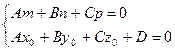- условия принадлежности прямой и плоскости.

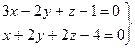Пример. Дана прямая и точка М₀(1, 0, –2). Через точку М₀ провести плоскость, перпендикулярную данной прямой. Уравнение искомой плоскости ищем в виде: A(x – 1) + B(y – 0) + C(z + 2) = 0. В данном случая , ,

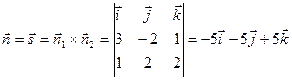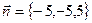-5(x – 1) – 5y + 5(z + 2) = 0, - x – y + z + 3 = 0.

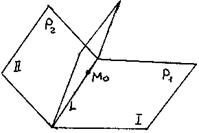
Пучок плоскостей.

Пучок плоскостей – множество всех плоскостей, проходящих через заданную прямую – ось пучка.

Чтобы задать пучок плоскостей, достаточно задать его ось. Пусть уравнение этой прямой задано в общем виде:

.

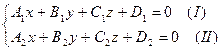Составить уравнение пучка – значит составить уравнение, из которого можно получить при дополнительном условии уравнение любой плоскости пучка, кроме, б.м. одной. Умножим II уравнение на л и сложим с I уравнением:

A₁x + B₁y + C₁z + D₁ + л(A₂x + B₂y + C₂z + D₂) = 0 (1) или

(A₁+ лA₂)x + (B₁+ лB₂)y + (C₁ + лC₂)z + (D₁ + лD₂) = 0 (2).

л – параметр – число, которое может принимать действительные значения. При любом выбранном значении л уравнения (1) и (2) линейные, т.е. это – уравнения некоторой плоскости.

1. Покажем, что эта плоскость проходит через ось пучка L. Возьмем произвольную точку M₀(x₀, y₀, z₀) 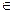L. Следовательно, М₀ 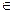Р₁ и М₀ 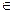Р₂. Значит:

.

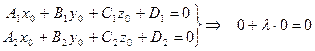Следовательно, плоскость, описываемая уравнением (1) или (2) принадлежит пучку.

2. Можно доказать и обратное: всякая плоскость, проходящая через прямую L, описывается уравнением (1) при соответствующем выборе параметра л.

Пример 1. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + y + 5z – 1 = 0 и 2x + 3y – z + 2 = 0 и через точку М(3, 2, 1).

Записываем уравнение пучка: x + y + 5z – 1 + л(2x + 3y – z + 2) = 0. Для нахождения л учтем, что М 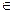Р:

3 + 2 + 5 – 1 + л(6 + 6 – 1 + 2) = 0 => л = 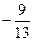, т.е.

x + y + 5z – 1 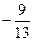(2x + 3y – z + 2) = 0, 5x + 14y – 74z + 31 = 0.

Пример 2 (Э). Составить уравнение плоскости, которая проходит через прямую 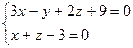и точку М₀ (4, -2, -3).

Запишем 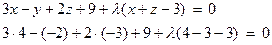; 17 + л = 0; л = -17

3x – y + 2z + 9 + 17x + 17z – 51 = 0; 20x – y + 19z – 42 = 0.

Пример 3 (Э). Составить уравнение плоскости, проходящей через прямую 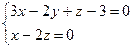перпендикулярно плоскости x – 2y + z + 5 = 0. 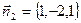; 3x – 2y + z – 3 + л(x – 2z) = 0; (3 + л)x – 2y + (1 – 2 л)z – 3 = 0; 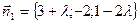; ; 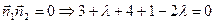л = 8; 11x – 2y – 15z – 3 = 0.