Основы логики предикатов первого порядка
Логика – наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Описания предметных областей, выполненные с помощью логических языков, называются логическими (формальными) моделями [2]. Основная идея подхода при построении логических моделей состоит в том, что вся информация, необходимая для решения прикладных задач, рассматривается как совокупность фактов (аксиом) и утверждений, которые представляются как формулы в некоторой логике. Знания отображаются совокупностью таких формул, а получение новых знаний сводится к реализации процедур логического вывода.
Логика предикатов первого порядка является дальнейшим развитием традиционной логики Аристотеля и логики высказываний. Одним из ключевых понятий логики высказываний является непосредственно высказывание – выражение, записанное с помощью определенного синтаксиса, которому можно приписать истинностное значение (истина или ложь). Например, выражения «В сутках 24 часа» или «Инопланетяне существуют» являются высказываниями, так как могут быть истинными или ложными (в зависимости от принятой объективной или субъективной точки зрения). При этом само выражение в логике высказываний представляется неделимым целым, т.е. его нельзя разделить на отдельные компоненты и соответственно использовать сведения об его структуре.
Логика предикатов позволяет расчленить высказывание, представленное в виде предиката, на предикатный символ[1] (выражение, означающее свойство сущности или тип отношения между сущностями) и терм/термы (выражение/выражения, означающие значение свойства сущности или связываемые отношением сущности). Непосредственным аналогом предиката в программировании является логическая (булева) функция, где имя функции – предикатный символ, а ее аргументы – термы. Например, в предикате (логической функции) «простое_число(X)»: «простое_число» – предикатный символ (имя функции), а «X» – терм (аргумент функции). При одних значениях X (например, 13 или 17) это высказывание истинно, при других (например, 10 или 18) – ложно.
Предикат первого порядка часто называют атомарной формулой (атомом), что означает неделимость предиката на подформулы, эквивалентные по своей семантике другому предикату. Номер порядка означает, что в качестве термов нельзя использовать другие предикаты. В то же время за счет использования логических операций (связок) предикаты можно объединять в более сложные высказывания.
Для элементов языка логики предикатов используется следующий синтаксис:
· логическая константа – true (истина) и false (ложь);
· константа – символьное выражение, начинающееся со строчной буквы (например, cat, blue);
· переменная – символьное выражение, начинающееся с прописной буквы или знака подчеркивания (например, X, Сat, _blue);
· функция и предикат – символьное выражение, начинающееся со строчной буквы, за которым следует список аргументов (термов), заключенных в скобки (например, кошка(катя), sin(X), друзья(вася, петя));
· список – упорядоченный набор элементов (константы, переменные или предикаты), указанных через запятую и заключенных в квадратные скобки (например, [red, blue], [X, Сat, _blue], [кошка(катя)]);
· терм – константа, переменная, функция или список;
· логическая операция:
o Ø – отрицание;
o Ù – логическое И (конъюнкция, логическое умножение);
o Ú – логическое ИЛИ (дизъюнкция, логическое сложение);
o ® (Þ) – импликация (если - то);
o « (º) – эквивалентность;
· квантор переменной – логический оператор, с помощью которого высказывание о какой-либо сущности преобразуется в высказывание о совокупности (множестве) таких сущностей:
o $ – квантор существования;
o " – квантор всеобщности;
· вспомогательный символ – круглые скобки, запятая, +, - и т. п.;
· формула (предложение, правило, правильно построенная формула) – предикат, логическое выражение или одна из следующих конструкций: ØА, AÙB, AÚB, A®B, A«B, ("X) A и ($X) А, где A и B – формулы,
а X – переменная. Результатом вычисления формулы является либо истина, либо ложь.
Приоритет операций и кванторов при исчислении формул показан ниже.
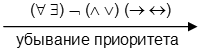
В скобках показаны операции (кванторы) с одинаковым приоритетом. Если в формуле используются операции (кванторы) с одинаковым приоритетом, то порядок исчисления слева-направо. Изменение порядка исчисления можно добиться за счет использования круглых скобок.
Примеры формул:
· если Маша мать X и Y, то X является братом или сестрой Y:
мать(маша, X) Ù мать(маша, Y) ® брат(X, Y) Ú сестра(X, Y).
· если X – человек, то он смертен:
человек(X) ® смертен(Х).
Квантор существования $ указывает, что предложение истинно, по крайней мере, для одного значения переменной. Например, $X друзья(X, петя) – существует, по крайней мере, один субъект X, который является другом Пети.
Квантор всеобщности " указывает, что предложение истинно для всех значений переменной. Например, "X человек(X) ® смертен(Х) – все люди смертны.
При комбинации кванторов важен порядок их использования. Например, для предиката любит(Х, Y), означающего, что X любит Y (обратное необязательно):
· "X$Y любит(Х, Y) – любой Х любит хотя бы одного Y;
· "Y$X любит(Х, Y) – любого Y любит хотя бы один Х;
· $X"Y любит(Х, Y) – существует такой Х, который любит всех;
· $Y"X любит(Х, Y) – существует такой Y, которого любят все;
· "X"Y любит(Х, Y) и "Y"Х любит(Х, Y) – любой X любит всех Y и любой Y любим всеми X (эквивалентные предложения);
· $X$Y любит(Х, Y) – существует такой X, который любит хотя бы одного Y;
· $Y$Х любит(Х, Y) – существует такой Y, которого любит хотя бы один X.
Основы Пролога
Наиболее известным языком логического программирования, реализующим модифицированную логику предикатов первого порядка, является Пролог (Prolog – PROgramming LOGig, логическое программирование). В нем отсутствует возможность использования кванторов, а составные формулы записываются в виде фраз Хорна.
Программа на Прологе состоит из предложений (формул), каждое из которых должно заканчиваться точкой. В общем случае предложение имеет вид:
B :- A1, ... , An.
B – заголовок или голова предложения, A1, ..., An – тело. В предложении ключевой логической операцией является перевернутая импликация
(B :- A эквивалентно B A). Символ «:-» означает «следует из», символ «,» – конъюнкция (логическое И, Ù).
При необходимости применения дизъюнкции (логическое ИЛИ, Ú) используется символ «;», действующий до следующей дизъюнкции, окончания правила или закрывающей круглой скобки.
Таблица 1
Примеры использования дизъюнкции в Прологе
| Логика предикатов | Пролог |
| (A1 Ù ... Ù An) Ú (B1 Ù ... Ù Bm) ® C | C :- A1, ... , An; B1, ... , Bm. |
| A Ù (B Ú C) ® D | D :- A, (B ; C). |
Предложения в Прологе бывают трех видов:
· факт – предложение, у которого нет тела. В терминах логики предикатов, факт – это и есть предикат. Например, факт, что Наташа является мамой Даши, может быть записан в виде[2]:
mama('Наташа', 'Даша').
· правило – предложение, истинность заголовка которого в виде предиката зависит от истинности одной или нескольких формул, указанных в теле. Например, бабушка человека – мама его мамы или мама его папы. Соответствующие правила будут иметь вид:
grandmama(X, Y):-
mama(X, Z), mama(Z, Y).
grandmama(X, Y):-
mama(X, Z), papa(Z, Y).
или
grandmama(X, Y):-
mama(X, Z), mama(Z, Y);
mama(X, Z), papa(Z, Y).
или
grandmama(X, Y):-
mama(X, Z), (mama(Z, Y); papa(Z, Y)).
· вопрос (запрос, цель) – предложение, состоящее только из тела. Автоматическая система логического вывода Пролога рассматривает вопрос как цель, к которой надо стремиться. Если цель будет достигнута, Пролог выдает положительный ответ (true), иначе – отрицательный (false). Обычно в интерпретаторах Пролога вопросы задаются в отдельном командном окне и перед каждым новым вопросом ставится «?-». Например, вопросы с ответами «Наташа является мамой Даши?» и «Кто является мамой Даши?» выглядят:
?- mama('Наташа', 'Даша').
true.
и
?- mama(X, 'Даша').
X='Наташа'.
Предложения, записанные с использованием перевернутой импликации, называются фразами Хорна. Разновидности предложений Пролога, записанные в виде фраз Хорна (B A), можно интерпретировать следующим образом:
· факт: B true;
· правило: B A;
· вопрос: true A.
Во всех предложениях можно использовать переменные. Считается, что переменные в теле одного правила неявно связаны квантором всеобщности.
Переменные могут быть свободными или связанными.
Свободная переменная – переменная, которая еще не получила значения. Она не равняется ни нулю, ни пробелу; у нее вообще нет никакого значения. Такие переменные называют также неконкретизированными.
Переменная, которая получила какое-то значение, называется связанной. Такой переменной не может быть присвоено новое значение, т. е., по сути, переменная становится константой.
Областью действия переменной в Прологе является одно предложение. В разных предложениях может использоваться одно и то же имя переменной для обозначения разных сущностей. Исключением из правила определения области действия является анонимная переменная, которая обозначается символом подчеркивания «_». Анонимная переменная предписывает интерпретатору (компилятору) проигнорировать значение аргумента (терма). Если в правиле несколько анонимных переменных, то все они отличаются друг от друга, несмотря на то, что записаны с использованием одного и того же символа «_». Анонимные переменные могут записываться только в качестве терма предиката. Использовать их в выражениях (например, арифметических) нельзя. Пример использования анонимной переменной в вопросе «Есть ли у Даши мама?»:
?- mama(_, 'Даша').
true.
Таким образом, программа на Прологе состоит из фактов и правил, выражающих некоторые знания о предметной области. Вопросы – предложения, истинность которых нас интересует. Если запрос не содержит переменных, то вычисление его значения дает ответ «true» при его истинности, либо ответ «false» при его ложности. Если же в вопросе есть переменные, то ищутся их значения (интерпретация), при которых это предложение и другие необходимые предложения программы становятся истинными.
Для поиска ответа на вопрос (доказательства целевого утверждения)
в Прологе используется метод перебора с возвратами[3] (поиск в глубину).
В то же время, за счет структуры и порядка формул можно добиться реализации поиска в ширину.
