Доказательство неразрешимости логики первого порядка методом Геделя

Для доказательства неразрешимости логики первого порядка достаточно продемонстрировать, как по данной машине Т с входным значением n (то есть когда машина находится на самой левой единице в сплошной последовательности из n единиц при пустых символах в остальных клетках ленты) построить такие предложение I и конечное множество предложений Г, что машина Т при входном значении 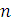останавливается тогда и только тогда, когда Г ├ I.

Не существует эффективной процедуры, позволяющей решать, останавливается ли произвольная машина Тьюринга Т при произвольном входном значении n и по данной машине Тьюринга Т можно построить примитивно рекурсивную функцию g, обладающую следующим свойством: какое бы n мы не взяли, g (n, t) = 0 в точности тогда, когда t – номер шага, более позднего, чем тот, на котором машина T останавливается, если ее запустить при входном значении n. (по определению функции g, если шаг t не таков, то g (x, t) = <a, b, c> = 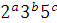для некоторых a, b, c и потому g (x, t) > 0. Если же t – такой шаг, то g (x, t) = 0.

Таким образом, если дана машина Т, то можно эффективно построить некоторую конечную последовательность q₀, q₁, …, q_r примитивно рекурсивных функций, удовлетворяющую двум условиям: 1) каждая функция g_i либо является базисной функцией, либо получается из некоторых предыдущих функций с помощью композиции или примитивной рекурсии и 2) для всякого n машина T, запущенная на входном значении n, в конце концов останавливается тогда и только тогда, когда g_r(n, t) = 0 для некоторого t.

Построим теперь по данной T последовательность примитивно рекурсивных функций, удовлетворяющую условиям 1) и 2). Каждой функции g_i поставим в соответствие свой функциональный символ g_i с тем же числом аргументов, что и g_i. Пусть g₀ = '. Используя эти символы, выпишем для каждого g_i одну или две очевидные формулы, определяющие функцию g_i Например,

если g_i = z, то "x g_i(x) = 0

если g_i = s, то "x g_i(x) = x'

если g_i = 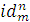, то "x₁ … "x_m … "x_n g_i(x₁, …, x_m, …, x_n) = x_m

Если g_i получается из предшествующих ей функций g_j и g_k c помощью примитивной рекурсии, то "x g_i(x, 0) =g_j(x) и "x "y g_i(x, y') =g_k(x, y, g_i(x, y))

Если же g_i получается из предшествующих ей функций g_о и 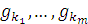путем композиции, то "x g_i(x) =g_j 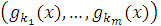(для краткости заменили здесь x₁, x₂, …, x_n на x, a "x₁, "x₂, …, "x_n на "x)

Запишем также формулы "x x ' ≠ 0 и "x "y (x ' = y ' → x = y). Обозначим теперь через Г множество всех этих формул, а через I – формулу .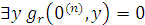

Утверждение. Машина T при входном значении 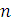останавливается тогда и только тогда, когда Г ├ I.

«Тогда». Пусть Г ├ I. Обозначим через 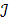модель, областью которой служит множество натуральных чисел и которая интерпретирует символ 0 как 0, а функциональные символы g_i – как 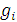. Все предложения из Г истинны в 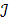. Поскольку Г ├ I, предложение I истинно также. Следовательно, для некоторого 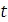справедливо 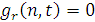. Согласно 2), T останавливается на .

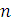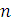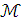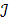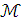«Только тогда». Предположим, что Т останавливается при входном значении . Для доказательства соотношения Г ├ I предположим, что – произвольная модель, в которой все предложения из Г истинны, и покажем, что из этого предположения следует истинность в . Пусть теперь 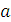– интерпретация символа 0 в модели 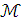, a – при всяком 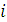– интерпретация в 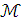символа g_i. Пусть, далее, 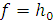(так что 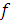– интерпретация в 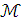символа ), и пусть 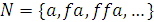. Так как формулы 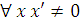и 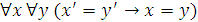истинны в 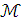, функция 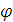, для которо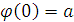й и 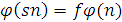, является изоморфизмом множества {0, 1, 2,…} натуральных чисел на множество N. Таким образом, можно считать, что N и является в действительности множеством натуральных чисел, 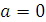, ограничение функции 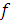на множество N есть 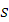, а потому всякий нумерал е обозначает число 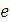в .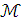

Индукцией по 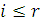легко доказывается, что для всех 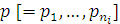р в N справедливо 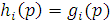(а потому 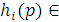N). Рассмотрим в деталях наиболее трудный случай, когда функция 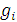получается примитивной рекурсией из функци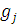й и 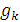причем 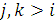. Итак, пусть для всех 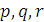из N выполняются равенства 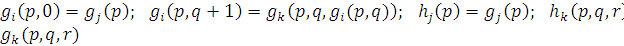.Нам нужно доказать, что 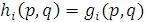для всех и 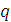. Но так как формулы 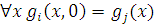и 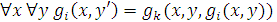содержатся в Г, справедливы равенства 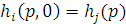и 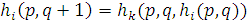. Но тогда 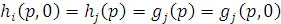и если 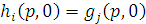, то, полагая 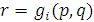, получим 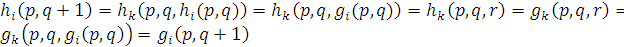. Таким образом, индукцией по 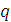заключаем, что 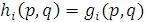для всех 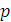и .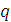

Поскольку 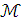при входном значении 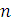останавливается, можно утверждать, что для некоторого 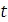справедливо 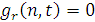, откуда 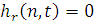, а потому 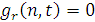истинно в 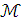, а значит, и I = 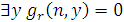истинно в 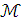, и доказательство заканчивается.

Заключение

Логика первого порядка обладает рядом полезных свойств, которые делают ее очень привлекательной в качестве основного инструмента формализации математики. Главными из них являются полнота (это означает, что для любой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием).

Логика первого порядка обладает свойством компактности: если некоторое множество формул невыполнимо, то невыполнимо также некоторое его конечное подмножество.

Являясь формализованным аналогом обычной логики, логика первого порядка дает возможность строго рассуждать об истинности и ложности утверждений и об их взаимосвязи, в частности, о логическом следовании одного утверждения из другого, или, например, об их эквивалентности.

В ходе исследования были рассмотрены основные понятия логики первого порядка и изучены доказательства неразрешимости логики первого порядка. Для этого было разобрано понятие машины Тьюринга, доказана неразрешимость проблемы ее остановки. На основе полученного выведена неразрешимость логики первого порядка. Так же разобрано доказательство неразрешимости логики первого порядка методом Геделя.