Глава 6. интеллектуальные технологии и системы

ЛОГИЧЕСКИЕ МОДЕЛИ

Основная идея подхода при построении логических моделейпредставления знаний состоит в том, что вся информация, необходимая для решения прикладных задач, рассматривается как совокупность фактов и утверждений, которые представляются как формулы в некоторой логике. Знания отображаются совокупностью таких формул, а получение новых знаний сводится к реализации процедур логического вывода.

В основе логических моделей представления знаний лежит понятие формальной теории, задаваемое четверкой: S = < В, F , A , R >, где В — счетное множество базовых символов (алфавит), F >— множество, называемое формулами, А — выделенное подмножество априори истинных формул (аксиом), R — конечное множество от ношений между формулами, называемое правилами вывода.

Достоинства логических моделей представления знаний:

1. В качестве «фундамента» здесь используется классический аппарат математической логики, методы которой достаточно хорошо изучены и формально обоснованы.

2. Существуют достаточно эффективные процедуры вывода, в том числе реализованные в языке логического программирования Пролог.

3. В базах знаний можно хранить лишь множество аксиом, а все остальные знания получать из них по правилам вывода.

Однако действительность не укладывается в рамки классической логики. Так называемая человеческая логика, применяемая при работе с неструктурированными знаниями, — это интеллектуальная модель с нечеткой структурой, и в этом ее отличие от «старой» (классической) логики. Таким образом, логики, адекватно отражающей человеческое мышление, к настоящему времени еще не создано.

ПРОДУКЦИОННЫЕ МОДЕЛИ

Психологические исследования процессов принятия решений человеком показали, что рассуждая и принимая решения, человек использует правила продукций, или продукционные правила (от англ. Production — правило вывода, порождающее правило).

В общем случае продукционное правило можно представить в следующем виде:

i : S; L; A→B; Q

где i — индивидуальный номер продукции;

S — описание класса ситуаций, в котором данная структура может использоваться;

L — условие, при котором продукция активизируется;

А→В — ядро продукции, например: «ЕСЛИ A1, A2,,..., Ап ТО В» . Такая запись означает, что «если все условия от A1 до Аn являются истиной, то В также истина» или же «когда все условия от A1 до Аn становятся истиной, то следует выполнить действие B»;

Q — постусловие продукционного правила, описывает операции и действия (процедуры), которые необходимо выполнить после выполнения В. Например, внести изменения в данные либо в саму продукцию.

Пример:

ЕСЛИ у является отцом х , ( A 1 )

z является братом у, ( A 2 )

ТО z является дядей х , (В)

В этом случае n =2. При n =0 получаем знания, состоящие только из вывода, то есть простой факт, например, «Атомный вес железа равен 55,8471». Суть использования правил продукции для представления знаний состоит в том, что левой части ставится в соответствие некоторое условие, а правой части — действие: ЕСЛИ <перечень условия>, ТО <перечень действий>. В такой интерпретации левая часть правил оценивается по отношению к базе данных (известному набору фактов) системы, и если эта оценка в определенном смысле соответствует логическому значению «ИСТИНА», то выполняется действие, заданное в правой части продукции.

В общем случае под условием понимается некоторое предложение — образец, по которому осуществляют поиск в базе знаний, а под действием — действия, выполняемые при успешном исходе поиска, — это могут быть реальные действия, если система управляющая, или заключение — вывод, представляющий собой новое (фактуальное) знание, или некоторая цель.

При использовании продукционной модели база знаний состоит из набора правил. Программа, управляющая перебором правил, называется машиной вывода. Механизм выводов связывает знания воедино, а затем выводит из последовательности знаний заключение.

Пример:

Пусть в базе знаний вместе с описанными выше знаниями содержатся еще и такие знания:

ЕСЛИ z является отцом х ,

z является отцом у,

х и у не являются одним и тем же лицом,

ТО х и у являются братьями;

где х , у, z - переменные.

Пусть также в базе данных (рабочей памяти) имеются факты:

α является отцом β ,

α является отцом γ ,

β является отцом δ .

Тогда из этих знаний можно формально вывести заключение, что

γ является дядей δ .

В продукционных системах, основанных на знаниях, процесс обработки информации может осуществляться двумя способами. Первый предполагает обработку информации в прямом направлении (метод сопоставления), когда образцом для поиска служит левая часть продукционного правила — условие, то есть задача решается в направлении от исходного состояния к целевому. Это соответствует стратегии «от данных к цели» или стратегии управления данными. После разрешения возникающих конфликтов выполняются правые части продукционных правил, что соответствует логическому выводу новых утверждений. После добавления выведенных утверждений в базу данных процедура повторяется. Процесс оканчивается, если выполняется продукционное правило, предписывающее прекращение поиска, или в базу данных поступает утверждение, являющееся решением. При втором подходе обработка информации осуществляется в обратном направлении — метод «генерации» или выдвижения гипотезы и ее проверки (стратегия «от цели к данным»). При каждом обратном движении возникает подцелевое состояние, из которого целевое может быть получено при прямом движении. В этом случае проверяются правые части продукционных правил с целью обнаружить в них искомое утверждение. Если такие продукционные правила существуют, то проверяется, удовлетворяется ли левая часть продукционного правила. Если да, то гипотеза считается подтвержденной, если нет — отвергается.

Таким образом, продукционные правила могут применяться к описанию состояния и описывать новые состояния (гипотезы) или же, напротив, использовать целевое состояние задачи как базу, когда система работает в обратном направлении. При этом продукционные правила применяются к целевому описанию для порождения подцелей (образуют систему редукций).

Пример:

Имеется фрагмент БЗ из двух правил:

П 1 : ЕСЛИ «отдых - летом» и «человек - активный»,

ТО «ехать в горы».

П 2 : ЕСЛИ «любит солнце»,

«отдых летом».

Предположим в систему поступили данные:

«человек - активный» и «любит солнце»

Прямой вывод:исходя из данных, получить ответ.

1-й проход:

Шаг 1. Пробуем П 1 не работает -

не хватает данных «отдых - летом».

Шаг 2. Пробуем П 2 , работает,

в базу поступает факт «отдых - летом».

2-й проход:

Шаг 3. Пробуем П 1 , работает,

активируя цель «ехать в горы», которая и выступает,

например, как совет, который дает система.

Обратный вывод:

подтвердить выбранную цель при помощи имеющихся правил и данных.

1-й проход:

Шаг 1. Цель - «ехать в горы»:

становятся новой целью, и имеется правило, где она в правой части.

Шаг 2. Цель «отдых летом»:

правило П ₂ подтверждает цель и активизирует ее.

2-й проход:

Шаг 3. Пробуем П ₁ , подтверждается искомая цель.

Свойства продукционных моделей:

Модульность — отдельные продукционные правила могут быть добавлены, удалены или изменены в базу знаний независимо от других; кроме того, модульный принцип разработки (сборки) продукционных систем позволяет автоматизировать их проектирование.

Каждое продукционное правило — самостоятельный элемент знаний (локальный источник знаний); отдельные продукционные правила связаны между собой только через поток данных, которые они обрабатывают.

Простота интерпретации — «прозрачная» структура продукционных правил облегчает их смысловую интерпретацию.

Естественность — знания в виде «что делать и когда» являются естественны ми с точки зрения здравого смысла.

Недостатки продукционных систем проявляются тогда, когда число правил становится большим и возникают непредсказуемые побочные эффекты от изменения старого и добавления нового правила. Кроме того, затруднительна оценка целостного образа знаний, содержащихся в системе.

Продукционные модели (наряду с фреймами) являются наиболее распространенными средствами представления знаний. Они близки к логическим моделям, что позволяет организовывать на их базе эффективные процедуры вывода, и в то же время более наглядно (чем классические логические модели) отражают знания. Продукционная модель чаще всего применяется в промышленных экспертных системах. Она привлекает разработчиков своей наглядностью, высокой модульностью, легкостью внесения дополнений и изменений и простотой логического вывода.

СЕМАНТИЧЕСКИЕ СЕТИ

Способ представления знаний с помощью сетевых моделейнаиболее близок к тому, как они представлены в текстах на естественном языке. В его основе лежит идея о том, что вся необходимая информация может быть описана как совокупность троек ( arb ), где а и b — объекты или понятия, а r — бинарное отношение между ними. Формально сетевые модели представления знаний могут быть заданы в виде

H = < I , C ₁ ,…, C_n , Г>, где

I — множество информационных единиц,

С ₁ ,..., С_п — множество типов связей между элементами

I , отображение Г задает между информационными единицами, входящими в I , связи из заданного набора типов связей {С _i }.

В зависимости от типов связей {С _i } различают:

· Классифицирующие сети — в них используются отношения структуризации, они позволяют вводить в базы знаний различные иерархические отношения между элементами множества I .

· Функциональные сети— вычислительные модели, характеризующиеся наличием функциональных отношений, они позволяют описывать процедуры вычислений одних информационных единиц через другие.

· Сценарии — в них используются каузальные отношения (причинно-следственные или устанавливающие влияние одних явлений или фактов на другие), а также отношения типов «средство — результат», «орудие — действие» и т. д.

Если в сетевой модели допускаются связи различного типа, то ее называют семантической сетью.

Термин «семантическая» означает «смысловая», а сама семантика — это наука, устанавливающая отношения между символами и объектами, которые они обозначают, то есть наука, определяющая смысл знаков.

Семантическая сеть —это модель, основой для которой является формализация знаний в виде ориентированного графа с размеченными вершинами и дугами. Вершинам соответствуют объекты, понятия или ситуации, а дугам — отношения между ними. Это наиболее общая модель представления знаний, так как в ней имеются средства реализации всех характерных для знаний свойств: внутренней интерпретации, структурированности, семантической метрики и активности.

Достоинства сетевых моделей: большие выразительные возможности; наглядность системы знаний, представленной графически; близость структуры сети, представляющей систему знаний, семантической структуре фраз на естественном языке; соответствие современным представлениям об организации долговременной памяти человека.

Недостатки: сетевая модель не дает (точнее, не содержит) ясного представления о структуре предметной области, которая ей соответствует, поэтому формирование и модификация такой модели затруднительны; сетевые модели представляют собой пассивные структуры, для обработки которых необходим специальный аппарат формального вывода и планирования. Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети поставленной задачи. Это, в свою очередь, обусловливает еще один недостаток модели — сложность поиска вывода на семантических сетях.

Еще раз подчеркнем, что сетевые модели являются очень наглядным и достаточно универсальным средством представления знаний. Однако их формализация в конкретных моделях представления, использования и модификации знаний оказывается достаточно трудоемкой, особенно при наличии множественных отношений между ее элементами.

ФРЕЙМОВЫЕ МОДЕЛИ

Термин фрейм( frame — каркас, рамка) предложен М. Минским в 70-е годы для обозначения структуры знаний для восприятия пространственных сцен. Эта модель, как и семантическая сель, имеет глубокое психологическое обоснование. Под фреймом понимается абстрактный образ или ситуация. В психологии и философии известно понятие абстрактного образа. Например, слово «комната» вызывает образ комнаты — «жилое помещение с четырьмя стенами, полом, потолком, окнами и дверью». Из этого описания ничего нельзя убрать, например, убрав окна, мы получим уже чулан, а не комнату. Но в нем есть «слоты», или «щели», — незаполненные значения некоторых атрибутов — количество окон, цвет стен, высота потолка, покрытие пола и др. Такой образ и называется фреймом (фреймом минимального описания). Фреймом называется также и формализованная модель этого образа.

Фреймовая модель,основанная на теории М. Минского, представляет собой систематизированную в виде единой теории технологическую модель памяти человека и его сознания. Важным элементом в этой теории является понятие фрейма — структуры данных для представления некоторого концептуального объекта. Информация, относящаяся к этому фрейму, содержится в составляющих фрейма — слотах. В отличие от моделей других типов, во фреймовых моделях фиксируется жесткая структура, которая называется протофреймом (фреймом-прототипом, или образцом). В общем случае фрейм определяется следующим образом:

f = [( r ₁ , v ₁ ,), … ,( r _n , v _n )], где

f — имя фрейма;

v_i — значение слота,

или

(ИМЯ ФРЕЙМА:

(имя 1-го слота: значение 1-го слота),

(имя 2-го слота: значение 2-го слота),

…

(имя n-го слота: значение n-го слота)).

Значением слота может быть практически что угодно (числа или математические соотношения, тексты на естественном языке или программы, правила вывода или ссылки на другие слоты данного фрейма). В качестве значения слота может выступать набор слотов более низкого уровня, что позволяет во фреймовых представлениях реализовать «принцип матрешки».

В качестве значения слота может выступать имя другого фрейма; так образуются сети фреймов. Все фреймы взаимосвязаны и образуют единую фреймовую структуру, в которой органически объединены декларативные и процедурные знания. Это дает возможность достаточно естественно производить композицию и декомпозицию информационных структур аналогично тому, как это делал бы человек при описании структуры своих знаний.

Кроме фреймов-образцов, или прототипов, хранящихся в базе знаний, различают фреймы-экземпляры, которые создаются для отображения реальных ситуаций на основе поступающих данных. При конкретизации (означивании) фрейма ему и слотам присваиваются конкретные имена, и происходит заполнение слотов. Таким образом, из протофреймов получаются фреймы-экземпляры.

Например, структура таблицы, содержащей список работников, записанная в виде протофрейма , имеет вид

(СПИСОК РАБОТНИКОВ:

Фамилия (значение слота 1);

Год рождения (значение слота 2);

Специальность (значение слота 3);

Стаж (значение слота 4).

Если в качестве значений слотов использовать реальные данные из таблицы, то получится фрейм-экземпляр.

Важнейшим свойством фреймов является заимствованное из теории семантических сетей наследование свойств. И во фреймах, и в семантических сетях наследование происходит по АКО-связям (от A Kind Of = это). Слот АКО указывает на фрейм более высокого уровня иерархии, откуда неявно наследуются, то есть переносятся значения аналогичных слотов, причем наследование свойств может быть частичным.

Фреймовые модели является достаточно универсальными, поскольку позволяют отобразить все многообразие знаний о мире:

· через фреймы-структуры для обозначений объектов и понятий (заем, залог, вексель);

· фреймы-роли (менеджер, кассир, клиент);

· фреймы-сценарии (банкротство, собрание акционеров, празднование именин);

· фреймы-ситуации (тревога, авария, рабочий режим устройства и т. д.).

Основными достоинствами модели фреймов как модели представления знаний являются способность отражать концептуальную основу организации памяти человека, а также естественность, наглядность представления, модульность, поддержка возможности использования значений слотов по умолчанию. Однако фрейм-представление является не конкретным языком представления знаний, а некоторой идеологической концепцией, реализуемой по-разному в различных языках. Теория фреймов послужила толчком к разработке нескольких языков представления знаний, которые благодаря своим широким возможностям и гибкости стали в последние годы довольно распространенными языками. Отметим, кроме того, что концепция объектно-ориентированного программирования может рассматриваться как реальное воплощение понятий, близких фрейму, в традиционных языках программирования.

Основным недостатком фреймовых моделей является отсутствие механизмов управления выводом. Отчасти этот недостаток устраняется при помощи присоединенных процедур, реализуемых силами пользователя системы.

Рассмотренные модели представления знаний во многом близки между собой. По сути, они обладают одинаковыми возможностями описывать и представлять знания. Разница состоит лишь в том, насколько удобно и естественно представлять те или иные знания в виде логических формул, семантических сетей, фреймов или продукций.

Если говорить о взаимосвязях рассмотренных выше моделей, то можно отметить следующее. Логические и продукционные модели отличаются достаточно выраженной процедурной формой, поэтому их часто используют для описания процедурных знаний. Вместо логического вывода, характерного для логических моде лей, в продукционных моделях используется вывод, основанный на знаниях. Модели знаний, опирающиеся на семантические сети, используют для описания декларативных знаний.

В системах искусственного интеллекта могут использоваться и несколько моде лей представления знаний одновременно. Например, в качестве значений некоторых слотов во фрейме могут выступать продукции. Именно смешанные представления оказываются наиболее многообещающими. В продукционных системах используются некоторые элементы логических и сетевых моделей. Поэтому они позволяют организовывать эффективные процедуры вывода (близость к логическим моделям) и наглядно отражать знания в виде сетей (близость к семантическим сетям). В них отсутствуют жесткие ограничения, характерные для логических исчислений, что дает возможность изменять интерпретацию элементов продукции. Кроме того, в результате применения правил вывода к фрагментам сетевого описания происходит трансформация сети за счет смены ее фрагментов, наращивание сети и исключение из нее ненужных фрагментов.

Фрейм можно рассматривать как фрагмент семантической сети, предназначенной для описания объекта (ситуации) проблемной области со всей совокупностью присущих ему свойств. Фреймовый подход к представлению знаний более жест кий, чем основанный на использовании семантической сети. Все то об объекте или ситуации, что важно с позиции решаемой задачи, не «размывается» в сети, а представляется во фрейме. В свою очередь, фрейм можно представить в виде сети, состоящей из вершин и дуг (отношений), так, что «нижние уровни» фрейма заканчиваются слотами, которые заполняются конкретной информацией при вызове фрейма.

Обобщая анализ моделей представления знаний, можно сделать два основных вывода:

Невозможно дать универсальные рекомендации по выбору модели. Выбор конкретной модели определяется возможностью и удобством представления исследуемой проблемной области с учетом необходимости не только представления, но и использования знаний. Однако чаще используются эвристические, не логические модели представления знаний.

Наиболее мощными оказываются смешанные представления.

ЭКСПЕРТНЫЕ СИСТЕМЫ, ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Современные экспертные системы широко используются для тиражирования опыта и знаний ведущих специалистов практически во всех сферах экономики. Традиционно знания существуют в двух видах — коллективный опыт и личный опыт. Если большая часть знаний в предлагаемой области представлена в виде коллективного опыта (например, высшая математика), эта предметная область не нуждается в экспертных системах. Если в предметной области большая часть знаний является личным опытом специалистов высокого уровня (экспертов), если эти знания по каким-либо причинам слабо структурированы, такая предметная область нуждается в экспертных системах.

Экспертные системы — это сложные программные комплексы, аккумулирующие знания специалистов в конкретных предметных областях и тиражирующие этот эмпирический опыт для консультаций менее квалифицированных пользователей. На рис. 6.1 изображены основные компоненты экспертной системы.

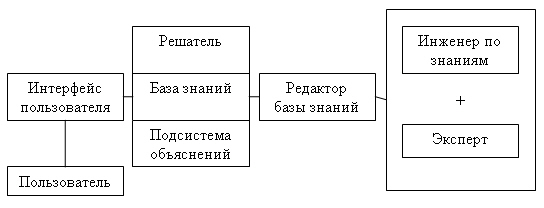
Рис. 6.1. Обобщенная структура экспертной системы

Пользователь — специалист предметной области, для которого предназначена система. Обычно его квалификация недостаточно высока, и поэтому он нуждается в помощи и поддержке со стороны экспертной системы.

Инженер по знаниям — специалист по искусственному интеллекту, выступает в роли промежуточного звена между экспертом и базой знаний (инженер-интерпретатор).

Интерфейс пользователя — комплекс программ, реализующий диалог пользователя с экспертной системой на стадии как ввода информации, так и получения результатов.

База знаний — ядро экспертной системы, совокупности знаний предметной области, записанная на машинный носитель в форме, понятной эксперту и пользователю (обычно на некотором языке, приближенном к естественному). Параллельно такому «человеческому» представлению существует база знаний во внутреннем «машинном» представлении.

Решатель — программа, моделирующая ход рассуждений эксперта на основании знаний, имеющихся в базе знаний.

Подсистема объяснений — программа, позволяющая пользователю получить ответы на вопросы: «Как была получена та или иная информация?» и «Почему система приняла такое решение?». Ответ на вопрос «Как?» — это трассировка всего процесса получения решения с указанием использованных фрагментов базы знаний, то есть всех шагов цепи умозаключения. Ответ на вопрос «Почему?» — ссылка на умозаключение, непосредственно предшествовавшее полученному решению, то есть отход на один шаг назад.

Интеллектуальный редактор базы знаний — программа, представляющая инженеру по знаниям возможность создавать базы знаний в диалоговом режиме.

Инструментальные средства построения экспертных систем:

о связано с тем, что парадигма объектно-ориентированного программирования тесно связана с фреймовой моделью представления знаний, кроме того, традиционные языки используются для создания других классов инструментальных средств искусственного интеллекта.

Языки искусственного интеллекта. Lisp, Prolog. Универсальность этих языков меньшая, чем у традиционных языков, но это компенсируется богатыми возможностями по работе с символьными и логическими данными, что крайне важно для задач искусственного интеллекта. На основе языков искусственно го интеллекта создаются специализированные компьютеры (например, Лисп- машины).

«Оболочки»( shells ) — «пустые» версии существующих экспертных систем, то есть готовые экспертные системы без базы знаний. Они вообще не требуют работы программистов для создания готовой экспертной системы. Требуются только специалисты в предметной области для заполнения базы знаний. Однако если некоторая предметная область плохо укладывается в модель, используемую в некоторой оболочке, заполнить базу знаний в этом случае весьма непросто.

Существующие компьютеры имеют принципы работы, в корне отличные от принципов работы человеческого мозга, поэтому основные надежды на развитие искусственного интеллекта связаны с построением нейрокомпьютеров.

НЕЙРОН, НЕЙРОННЫЕ СЕТИ, ОСНОВНЫЕ ПОНЯТИЯ

Нейрон (формальный, искусственный) —элементарный преобразующий элемент, как составная часть нейросети, в свою очередь, состоит из элементов трех типов и выполняет две основные функции — взвешенное суммирование и нелинейное пре образование. Элементы нейрона — умножители (синапсы), сумматор и нелинейный преобразователь. Синапсы осуществляют связь между нейронами, умножают входной сигнал (x_j ) на число, характеризующее силу связи, — вес синапса ( w_j ). Сумма тор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов и внешних входных сигналов. Нелинейный преобразователь выполняет нелинейную функцию одного аргумента — выхода сумматора. Таким образом, нейрон в целом реализует скалярную функцию векторного аргумента.

Функционирование нейрона можно разбить на два такта (в соответствии с двумя его функциями):

1. В сумматоре вычисляется величина возбуждения, полученного нейроном, 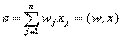(для простоты смещение w0 не учитывается).

2. Возбуждение пропускается через преобразующую (активационную) функцию f(•), в результате чего определяется выходной сигнал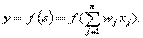

На рис. 76.2 представлена укрупненная схема нейрона.

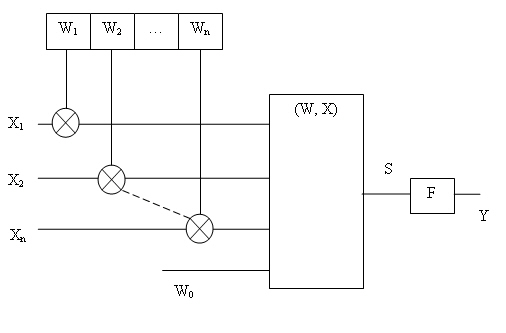
Рис. 6.2. Структурная схема нейрона

Наиболее часто используются следующие функции активации:

1. Пороговая (ступенчатая) функция 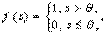где θ — порог срабатывания нейрона.

Концептуально каждый нейрон может рассматриваться, как ПРАВИЛО «ЕСЛИ (w, x) > θ и, ТО выдать импульс». Следует отметить, что, например, «небольшая» нейронная сеть для распознавания образов может содержать десятки миллионов нейронов. Обработка базы знаний, содержащей такое число правил, трудно реализуема даже на современных процессорах.

2. Сигмоидная ( логистическая )функция. Функция называется сигмоидной , если она ограничена по минимальному и максимальному значениям и имеет везде положительную производную. Кроме этого предполагается, что функция быстро сходится к верхнему пределу при s →+∞ и к нижнему при s →-∞. На пример, 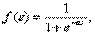где а — параметр (а > 0), 0 < f ( s ) < 1.

График сигмоидной функции качественно близок к изображению передаточной характеристики биологического нейрона. Сигмоидная функция приближается к ступенчатой с порогом θ = 0 при a →+ ∞. Очевидно, пороговая функция более удобна при аппаратной реализации нейрона, тогда как сигмоидная функция предпочтительна в аналитических исследованиях, поскольку она монотонна, всюду дифференцируема и имеет непрерывные производные любого порядка. Так ,f’ = af (1-f).

3. Гиперболический тангенс f (s) = th ( as) = 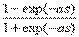, -1<f(s)<1. Свойство не четности тангенса, а также то, что f (0), иногда оказывается очень удобным.

Таким образом, каждый нейрон характеризуется вектором весовых множителей и параметрами преобразующей функции. Нейрон способен получать сигналы и в зависимости от их интенсивности и собственных характеристик выдавать выход ной сигнал. При этом если выходной сигнал нейрона близок к единице, то говорят, что нейрон возбужден.

Под нейронной сетью обычно понимается структура, состоящая из связанных между собой нейронов, аксиоматическое определение которых было дано ранее. К настоящему времени предложено большое количество способов объединения нейронов в нейросеть (при этом говорят о «топологии» нейросети ).

Не ограничивая общности, можно считать, что нейроны в сети расположены слоями. Обычно выделяют входной слой, на который подается возбуждающий сигнал, выходной слой, с которого снимают переработанный сетью сигнал, а все остальные слои называют скрытыми (поскольку они не видны пользователю). Очевидно, что для адекватного решения задачи функционирования сети нужно правильно выбрать значения весов связей между нейронами — обучить сеть.

Возможны несколько типов классификации существующих нейросетей. Наиболее часто используются следующие:

- по типу входной информации:

· сети, анализирующие двоичную информацию;

· сети, оперирующие с действительными числами;

- по методу обучения:

· сети, которые для того чтобы удовлетворять поставленным критериям требуют предварительного обучения перед включением их в реальную обстановку, — модели с учителем;

· сети, не требующие предварительного обучения, способные самообучаться (совершенствовать свои характеристики) в процессе работы;

- по характеру распространения информации:

· однонаправленные сети, в которых информация распространяется только в одном направлении от одного слоя элементов к другому;

· рекуррентные сети, в которых выходной сигнал элемента может вновь по ступать на этот элемент и другие элементы сети этого же или предыдущих слоев в качестве входного сигнала (сети с обратными связями);

- по способу преобразования входной информации:

· автоассоциативные;

· гетероассоциативные.

Они отличаются следующим. На всей сети или на одном ее слое задаются в определенный момент времени исходные состояния нейронов x =(x₁ , x₂ ,…, x_n ) то есть задается входной образ. Затем этот образ трансформируется в соответствии с функциями преобразования элементов. Информация распространяется по сети, происходит ее обработка. В однонаправленных сетях информация распространяется от слоя к слою, и выходной слой выдает результирующий вектор y =(y₁ , y₂ , …, y_m ) . (В однослойных сетях происходит стабилизация сети в одном из состояний.) После этого считываются значения узлов сети, представляющих выходной вектор. Возможны два варианта:

· х ≠ у — гетероассоциативная сеть, осуществляющая отображение входного вектора х в выходной вектор у;

· входной вектор х представляет искаженный или сжатый образ эталона x _>0 .

Такая сеть называется автоассоциативной.

Выходной вектор, получающийся в результате работы нейросети, характеризует состояние элементов сети. Смысл, который имеют значения этого вектора, определяется в зависимости от решаемой проблемы.

Решение задачи на нейрокомпьютере принципиально отличается от решения той же задачи на обычной ЭВМ. Решение задачи на обычной ЭВМ заключается в обработке вводимых данных в соответствии с априори разработанной и записанной в нее программой. Для составления программы необходимо разработать алгоритм, то есть определенную последовательность математических и логических действий, необходимых для решения этой задачи. Алгоритмы и программы разрабатываются людьми, а компьютер используется лишь для выполнения большого количества элементарных операций: сложения, умножения, проверки логических условий и т. п.

Нейрокомпьютер же используется как «черный ящик», который можно обучить решению задач из какого-нибудь класса. Нейрокомпьютеру «предъявляются» исходные данные задачи и ответ, который соответствует этим данным. Нейрокомпьютер должен сам построить внутри себя алгоритм решения этой задачи, чтобы выдать ответ, совпадающий с правильным . Естественно ожидать, что чем больше различных пар (исходные данные — ответ) будет предъявлено нейрокомпьютеру, тем более адекватную решаемой задаче модель он сформулирует. Более того, если после этапа обучения нейрокомпьютеру предъявить исходные данные, которых он раньше не встречал, то желательно, чтобы он, тем не менее, выдал правильное решение. В этом заключается способность нейрокомпьютера к обобщению. Поскольку в основе устройства нейрокомпьютера лежит искусственная нейросеть, то процесс обучения состоит в настройке параметров этой сети. При этом, как правило, топология сети считается неизменной, а к подстраиваемым параметрам обычно относятся параметры нейронов и величины синаптических весов. Обычно в литературе под обучением принято понимать процесс изменения весов связей между нейронами.

Классификация методов обучения нейронных сетей:

- по способу использования учителя:

· с учителем. Сети предъявляются примеры входных и выходных данных. Сеть преобразует входные данные и сравнивает свой выход с желаемым. После этого проводится коррекция весов с целью получить лучшую согласованность выходов;

· с последовательным подкреплением знаний. В этом случае сети не дается желаемое значение выхода, а только ставится оценка, хорош выход или плох;

· без учителя. Сеть сама вырабатывает правила обучения путем выделения оценочных признаков из набора входных данных;

- по использованию элементов случайности:

· детерминированные методы. В них шаг за шагом осуществляется процедура коррекции весов сети, основанная на использовании их текущих значений, входов сети, выходов нейронов и некоторой дополнительной информации, например значений желаемых выходов сети;

· стохастические методы. Они основываются на использовании случайных изменений весов в ходе обучения.

МОДЕЛИ НЕЙРОННЫХ СЕТЕЙ

ПОЛНОСВЯЗНЫЕ СЕТИ ХОПФИЛДА

Сеть Хопфилда (представлена на рис. 6.4) — однослойная сеть. Все нейроны связаны друг с другом связями w_ij , причем сигнал с выхода нейрона может подаваться на его же вход и необязательно w_ij = w_ji .

Рис. 6.4. Полносвязная сеть Хопфилда

Поскольку сигнал с выхода каждого нейрона подается на входы всех остальных, входной вектор начинает циркулировать, преобразуясь по сети до тех пор, пока сеть не придет в устойчивое состояние (то есть когда все нейроны на каждом последующем цикле будут вырабатывать тот же сигнал, что и на предыдущем). Очевидно, возможны случаи бесконечной циркуляции входного вектора без достижения устойчивого состояния.

Выберем функцию элементов в виде:

Состояние сети — множество текущих значений сигналов х от всех нейронов. Функционирование сети геометрически может быть представлено как движение вектора х , характеризующего состояние сети, на кубе [0,1]^п. Когда подается но вый входной вектор, сеть переходит из вершины в вершину, пока не стабилизируется. Устойчивая вершина определяется сетевыми весами, текущими входами и величиной порога. Если входной вектор частично неправилен или неполон, то сеть стабилизируется в вершине, ближайшей к желаемой.

В общем случае все возможные состояния сети образуют некое подобие холмистой поверхности, а текущие состояния сети аналогичны положениям тяжелого шарика, пущенного на эту поверхность, — он движется вниз по склону в ближайший локальный минимум. Каждая точка поверхности соответствует некоторому сочетанию активностей нейронов в сети, а высота подъема поверхности в данной точке характеризует «энергию» этого состояния. Энергия данного сочетания активностей определяется как сумма весов связей между парами активных нейронов, взятая со знаком минус (при 0 = 0).

Таким образом, если связь между двумя какими-то нейронами имеет большой положительный вес, то сочетания, в которых эти нейроны актив