Несущие изогнутые сетчатые плоскости В.Г. Шухова
Говоря об инженерном и изобретательском творчестве вообще и о Шухове в частности, часто главный упор делают на здравый смысл, как компас в работе. Но в этом случае многое может оказаться вне поля зрения, что не устроило бы инженера столь большого масштаба. Только на подлинно научной основе можно прийти к принципиально новому, к парадоксальным выводам и решениям.
Сочетание качеств опытного практика и хорошего теоретика помогло В. Г. Шухову подходить к созданию новых конструкторских форм на основе научного анализа возможных технических решений в широком диапазоне, их обстоятельной математической обработки.
На исходе XIX столетия появилась новая форма конструкции: регулярные поверхности двоякой отрицательной кривизны, получившие название гиперболоида (рис. 1) и гиперболического параболоида (ГИПАР) (рис. 2). Эти регулярные поверхности были известны в математике с давних пор. 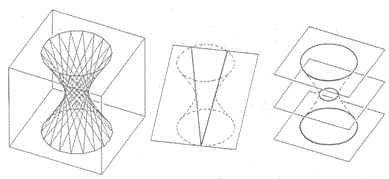
Рис.1. Гиперболоид и его характеристические сечения.
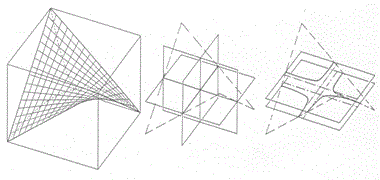
Рис.2. Гиперболический параболоид и его характеристические сечения.
Независимо друг от друга русский инженер В. Г. Шухов и каталонский архитектор Антони Гауди (1852—1926 гг.) выявили конструктивные и производственно-технические преимущества применения таких поверхностей в строительстве. Шухов построил в 1896 г. на Всероссийской выставке в Нижнем Новгороде свою первую башню в виде гиперболоида. Архитектор Гауди, известный своеобразным оформлением зданий в Барселоне, был, кроме того, и выдающимся конструктором. После первых шагов по изучению формообразования (предположительно в 1884 г.) он с 1909 г. начал применять гиперболический параболоид — перекошенную (в трех измерениях) плоскость — как конструкционное решение для форм стен и сводов кирпичных построек.
Тому, что гиперболоид и гиперболический параболоид Шухова — Гауди из регулярных поверхностей и других форм строительных конструкций оказались наиболее предпочтительными, имеются две причины. Первая связана с тем, что их седловидная форма придает даже тонкостенным пространственным конструкциям сравнительно высокую устойчивость. Второй практической причиной их применения в строительстве является то, что эти перекошенные поверхности можно просто изготовить из прямых элементов. Ведь, согласно определению, регулярные поверхности двоякой кривизны образуются в результате перемещения прямой образующей по двум направляющим. При образовании указанных форм в строительстве на смену плоскости (простой поверхности) приходит сетка или решетка с одинаковым шагом линейных элементов. Статические анализы Шухова все дальше уводили его от конструкций «иерархического типа» (стойки, прогоны, стропила, обрешетины и др.) к изогнутым сетчатым плоскостям, которые могли быть изготовлены из одинаковых элементов с ячейками или шагом (рис. 3) примерно такого же размера. Сетчатые башни в форме гиперболоидов явились составной частью этого процесса развития [5].
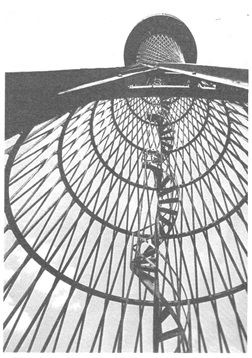
Рис.3. Водонапорная башня Шухова в Полибино. Получение поверхности двоякой кривизны с помощью прямых стержневых элементов.
Во времена бурного развития машиностроения естественным было воздействие его концепций (механики) на принципы конструирования инженерных сооружений (статику). Действительно, обнаруживается связь механического движения с геометрией регулярных поверхностей. В качестве примера можно назвать вращение, трансляцию или перенос (перемещение вдоль прямой или кривой) и винтовое движение по спирали. Шухов множество раз успешно использовал этот вид формообразования для разработки новых конструкционных форм.
Графическая статика, получившая к тому времени достаточное развитие, привела инженера и использующего инженерный подход архитектора к формам, возникающим не из геометрии, а из силового поля. Это формы, которые не установлены изначально в своих пропорциях (как, например, квадрат, круг или стрельчатая арка), а освобождены от этих ограничений и могут быть созданы с помощью статического метода в соответствии с силами, действующими на конструкцию.
