Суждения и отношения между ними
КОНТРОЛЬНЫЕ ЗАДАНИЯ
ПО МАТЕМАТИКЕ
Для студентов педагогического факультета
Могилев 2006
Пособие содержит задания по всем основным темам курса математики для педагогического факультета, по каждой теме – 25 вариантов.
Задания могут использоваться для составления контрольных работ, проведения зачетов, организации самостоятельной и индивидуальной работы студентов как заочного отделения, так и дневного.
С О Д Е Р Ж А Н И Е
| Номер задания | Т е м а | Стр. |
| 1. | Суждения и отношения между ними. | |
| 2. | Логическая функция и ее область истинности. | |
| 3. | Умозаключения, основанные на правилах логического следования. | |
| 4. | Операции над числовыми множествами. | |
| 5. | Разбиение множества на классы. Отношения между множествами | |
| 6. | Соответствие между множествами. Виды соответствий. | |
| 7. | Бинарное отношение на множестве. Свойства отношений. | |
| 8. | Теоретико-множественный смысл арифметических операций. | |
| 9. | Теоретико-множественное обоснование правил, связанных с операциями сложения и вычитания. | |
| 10. | Свойства арифметических операций. | |
| 11. | Связь между компонентами арифметических операций. | |
| 12. | Аксиоматический смысл арифметических операций. | |
| 13. | Метод математической индукции. | |
| 14. | Системы счисления. | |
| 15. | НОД и НОК целых неотрицательных чисел. | |
| 16. | Делимость целых неотрицательных чисел. | |
| 17. | Арифметические действия над действительными числами. | |
| 18. | Системы и совокупности неравенств с одной переменной. | |
| 19. | Системы уравнений с двумя переменными. | |
| 20. | Системы неравенств с двумя переменными. | |
| 21. | Свойства геометрических фигур (вычисления). | |
| 22. | Свойства геометрических фигур (доказательства). | |
| 23. | Геометрические преобразования (осевая симметрия). | |
| 24. | Геометрические преобразования (параллельный перенос, центральная симметрия). | |
| 25. | Геометрические преобразования (гомотетия, поворот). |
Суждения и отношения между ними
Два суждения заданы своими логическими формулами.
а) Установите отношения между этими суждениями.
б) Сформулируйте суждения, соответствующие этим формулам.
1. А Ú В Ú С и A Ú (Ø B É C)
2. Ø В ~ (Ø С Ú Ø А) и (Ø A É B) Ú (А É C)
3. А Ú В Ù С и A Ù Ø (B É C)
4. А Ù В Ù С и (A É Ø B) Ú C
5. Ø A Ù (B ~ C) и Ø А É В Ú С
6. Ø A Ú B É C и A É В Ù Ø С
7. A Ù (Ø B Ú Ø C) и A Ú (В ~ Ø С)
8. Ø A Ú (Ø B É Ø C) и Ø А Ù С ~ B
9. Ø A ~ Ø B Ú Ø C и В Ù С Ù Ø А
10. A É Ø (B Ù C) и А Ù С Ú Ø В
11. A Ù Ø B É Ø C и С ~ А Ú В
12. A Ú B É Ø C и Ø А É ØВ Ù С
13. Ø A Ù (Ø B ~ C) и Ø А Ú Ø(С É В)
14. Ø A É B Ù C и Ø С Ú А Ù В
15. A Ú (B É C) и Ø А Ù С É В
16. A É (B É C) и Ø (А Ù В) Ú С
17. A ~ B É C и А Ú Ø (В Ù Ø С)
18. A É B Ú C и А Ù (В ~ С)
19. С Ú Ø (А Ú В) и А Ù Ø В É Ø С
20. A Ú B ~ Ø C и Ø А Ù В É Ø С
21. Ø A Ù Ø B) Ú C и (Ø В ~ С) Ú А
22. Ø A É B Ù Ø C и А Ú Ø (В É С)
23. (A ~ Ø С) Ù Ø В и А Ù Ø (В É Ø С)
24. (B Ú Ø C) Ù Ø A и С É Ø (А Ù В)
25. Ø A Ù Ø B ~ C и Ø В Ù С É А
Разбиение множества на классы.
Отношения между множествами
1. При опросе 100 депутатов оказалось: английский язык знают 30 человек, немецкий – 40, только английский и немецкий языки –10 человек, только немецкий и французский –12 человек, только английский и французский – 8 человек, только немецкий – 14 человек; 20 депутатов не знают ни одного из названных иностранных языков.
Пусть I – множество опрошенных депутатов;
А – множество депутатов, которые знают английский язык;
В – множество депутатов, которые знают французский язык;
С – множество депутатов, которые знают немецкий язык.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
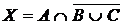 и
и 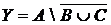
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько депутатов знают не менее двух иностранных языков?
2. При опросе 70 учеников оказалось: увлекаются спортом 22 человека, поют в хоре – 32 человека, занимаются в драмкружке 27 человек; 10 учеников посещают драмкружок и поют в хоре, 6 – поют в хоре и занимаются спортом, 8 спортсменов посещают драмкружок, 3 ученика занимаются спортом, поют в хоре и ходят в драмкружок.
Пусть: I – множество опрошенных учеников;
А – множество учеников, которые посещают драмкружок;
В – множество учеников, поющих в хоре;
С – множество учеников, которые занимаются спортом.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
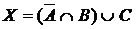 и
и 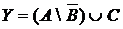
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько учеников занимаются только в одном кружке ?
3. Из 40 студентов педфака во время сессии получили "6" по белорусскому языку 19 человек, по философии – 22 человека, 4 студента поучили “6” только по белорусскому языку, 11 – только по философии, 5 – только по математике; 7 студентов получили "6" по философии и математике, 5 из них имеют оценку «6» и по белорусскому языку.
Пусть: I – множество студентов педфака;
А – множество студентов, которые получили "6" по математике;
В – множество студентов, которые получили "6" по белорусскому языку;
С – множество студентов, которые получили "6" по философии.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
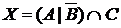 и
и 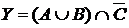
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько студентов получили не более одной шестерки?
4. Из 100 студентов 26 изучают немецкий язык, 48 – французский, 23 студента изучают немецкий, но не английский язык, 16 – только немецкий, 8 – немецкий и французский и также 8 – английский и французский; 24 студента не изучают ни одного из этих языков.
Пусть: I – множество опрошенных студентов;
А – множество студентов, изучающих английский язык;
В – множество студентов, изучающих французский язык;
С – множество студентов, изучающих немецкий язык.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
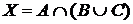 и
и 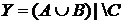
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько студентов изучают только один иностранный язык?
5. Из 50 студентов педфака досрочно сдали зачет по математике 19 человек, по педагогике – 21 человек, по философии – 12, 8 студентов сдали зачет по педагогике и философии, 5 – по математике и философии, 4 – по математике и педагогике, 3 студента получили зачет по всем этим дисциплинам.
Пусть: I – множество студентов педфака;
А – множество студентов, сдавших зачет по математике;
В – множество студентов, сдавших зачет по педагогике;
С – множество студентов, сдавших зачет по философии.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
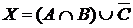 и
и 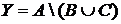
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько студентов сдали только два зачета?
6. В классе 38 учеников. Из них 16 занимаются футболом, 18 – хоккеем, 15 – волейболом; 8 учеников увлекаются футболом и волейболом, 4 – футболом и хоккеем, 5 – хоккеем и волейболом и 5 учащихся не занимаются спортом.
Пусть: I – множество учеников в классе;
А – множество учеников, которые занимаются футболом;
В – множество учеников, которые занимаются хоккеем;
С – множество учеников, которые занимаются волейболом.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
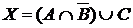 и
и 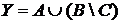
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько учеников занимаются только одним видом спорта?
7. При опросе 100 учеников оказалось: 19 учеников занимаются только лыжами, 20 – только коньками, 30 – только гимнастикой; 9 учеников занимаются лыжами и коньками, но не гимнастикой, 6 – лыжами и гимнастикой, но не коньками, 5 – гимнастикой и коньками, но не лыжами, 9 учеников не занимаются ни одним из указанных видов спорта.
Пусть: I – множество опрошенных учеников;
А – множество учеников, которые занимаются лыжами;
В – множество учеников, которые занимаются коньками;
С – множество учеников, которые занимаются гимнастикой.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
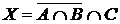 и
и 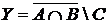
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько учеников занимаются только одним видом спорта?
8. В группе 28 студентов. Из них 4 отличника, 18 – поют в хоре, 14 –занимаются спортом; 3 студента-отличника поют в хоре, 2 студента-отличника занимаются спортом, 10 студентов только поют в хоре, 1 студент–отличник поет в хоре и занимается спортом.
Пусть: I – множество студентов группы;
А – множество студентов –отличников;
В – множество студентов, которые поют в хоре;
С – множество студентов, которые занимаются спортом.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
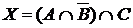 и
и 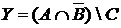
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько студентов–отличников не поют в хоре?
9. При опросе 110 человек оказалось: 44 человека знают английский язык, 50 – немецкий, 49 – французский; 14 человек знают английский и французский языки, 12 – французский и немецкий, 13 – английский и немецкий; 5 человек знают все три языка.
Пусть: I – множество опрошенных людей;
А – множество людей, знающих английский язык;
В – множество людей, знающих немецкий язык;
С – множество людей, знающих французский язык.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
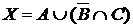 и
и 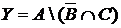
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько человек не знают ни одного из названых языков?
10. При опросе 100 депутатов оказалось: 63 человека увлекаются теннисом, 20 – лыжами, 25 – футболом; теннисом и футболом – 18, футболом и лыжами – 13, теннисом и лыжами – 12; 10 человек занимаются всеми названными видами спорта.
Пусть: I – множество опрошенных депутатов;
А – множество депутатов, которые занимаются теннисом;
В – множество депутатов, которые занимаются лыжами;
С – множество депутатов, которые занимаются футболом.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
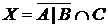 и
и 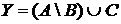
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько депутатов увлекаются только одним видом спорта?
11. Дано 80 натуральных чисел. Среди них 29 – четные, 23 – делятся на 5; 17 четных чисел не делятся на 3; 11 четных чисел не делятся ни на 5, ни на 3; 9 четных чисел делятся на 5; 7 чисел делятся на 3 и на 5; 22 числа не делятся ни на 2, ни на 3, ни на 5.
Пусть: I – множество данных натуральных чисел;
А – множество четных чисел;
В – множество чисел, которые делятся на 5;
С – множество чисел, которые делятся на 3.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
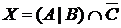 и
и 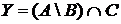
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько нечетных чисел делятся на 3 и 5?
12. Из 80 студентов педфака 29 занимаются в драмкружке, 23 – поют в хоре, 31 – занимаются танцами; 12 студентов из драмкружка занимаются танцами, 9 поют в хоре и посещают драмкружок, 7 поют в хоре и танцуют; 3 студента занимаются всеми тремя видами художественной самодеятельности.
Пусть: I – множество студентов педфака;
А – множество студентов, которые занимаются в драмкружке;
В – множество студентов, которые поют в хоре;
С – множество студентов, которые занимаются танцами.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
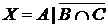 и
и 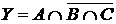
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько студентов занимаются только двумя видами деятельности?
13. Среди 80 геометрических фигур имеется: красных – 29, треугольных – 31, больших – 23; красных треугольников – 12, красных и больших фигур – 9, больших треугольников – 7; 9 красных треугольников не являются большими.
Пусть: I – множество данных геометрических фигур;
А – множество красных фигур;
В – множество треугольных фигур;
С – множество больших фигур.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
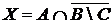 и
и 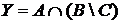
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько треугольных фигур не являются красными?
14. Среди 60 опрошенных учеников 11 класса увлекаются музыкой 21 человек, танцами – 23; 5 человек любят танцы и компьютерные игры, 4 – танцы и музыку, 15 – только музыку, 16 – любят музыку, но не любят компьютеры; 14 учеников не увлекаются ни музыкой, ни танцами, ни компьютерами.
Пусть: I – множество опрошенных учеников;
А – множество учеников, которые увлекаются музыкой;
В – множество учеников, которые увлекаются танцами;
С – множество учеников, которые увлекаются играми.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
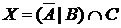 и
и 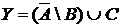
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько учеников любят только музыку и танцы?
15. Среди 60 геометрических фигур имеется: 21 синяя, 23 квадратных. При этом 17 квадратов не являются синими и не являются большими; 1 синий квадрат не является большим; 2 больших квадрата не являются синими и 2 большие синие фигуры не являются квадратами; 11 фигур не являются ни синими, ни большими, ни квадратным.
Пусть: I – множество геометрических фигур;
А – множество синих фигур;
В – множество квадратных фигур;
С – множество больших фигур.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
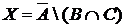 и
и 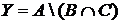
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько синих фигур не являются квадратными?
16. Среди 40 геометрических фигур 26 желтых, 25 больших, 27 круглых, 15 желтых и больших, 18 больших и круглых, 16 желтых и круглых, 1 фигура не является ни круглой, ни большой, ни желтой.
Пусть: I – множество геометрических фигур;
А – множество желтых фигур;
В – множество круглых фигур;
С – множество больших фигур.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
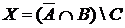 и
и 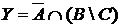
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько фигур являются круглыми или желтыми?
17. Из 40 студентов сдали экзамен по математике 26 человек, по педагогике – 25; 5 студентов сдали экзамен по математике и педагогике, но не сдали по философии; 8 – сдали по педагогике и философии и не сдали по математике; 6 – сдали по математике и философии и не сдали по педагогике; 2 студента сдали только по педагогике, 1 студент не сдал ни одного экзамена.
Пусть: I – множество студентов;
А – множество студентов, которые сдали экзамен по математике;
В – множество студентов, которые сдали экзамен по педагогике;
С – множество студентов, которые сдали экзамен по философии.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
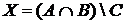 и
и 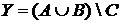
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько студентов сдали не менее двух экзаменов?
18. Дано 110 натуральных чисел. Среди них 44 четных, 46 делятся на 5, 49 делятся на 3, 13 четных чисел делятся на 5, 15 четных чисел делятся на 3; 14 чисел делятся на 5 и на 3, из них 3 – четные.
Пусть: I – множество данных натуральных чисел;
А – множество четных чисел;
В – множество чисел, которые делятся на 5;
С – множества чисел, которые делятся на 3.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
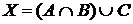 и
и 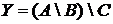
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько четных чисел не делятся ни на 3, ни на 5?
19. Среди 108 натуральных чисел имеется: 44 двузначных числа, 49 чисел делятся на 3, 19 двузначных чисел не делятся ни на 3, ни на 5; 22 числа делятся на 5, но не делятся на 3 и не являются двузначными; 23 числа делятся на 3, но не делятся на 5 и не являются двузначными; 3 двухзначных числа делятся на 3 и на 5, а 9 двузначных чисел делятся только на 5.
Пусть: I – множество данных натуральных чисел;
А – множество двузначных чисел;
В – множество чисел, которые делятся на 5;
С – множество чисел, которые делятся на 3.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
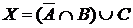 и
и 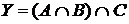
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько двузначных чисел делятся на 3 или 5?
20. При опросе 50 учеников оказалось: 16 человек увлекаются математикой, 11 – химией, 22 – иностранным языком, причем 7 математиков занимаются и химией, 5 химиков и 4 математика любят иностранный язык, 15 учеников не отдают предпочтения ни одному из названных предметов.
Пусть: I – множество опрошенных учеников;
А – множество учеников, которые увлекаются математикой;
В – множество учеников, которые увлекаются химией;
С – множество учеников, которые любят иностранный язык.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
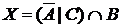 и
и 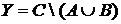
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько учеников любят математику или химию?
21. Из 78 студентов педфака 30 занимаются музыкой, 28 посещают драмкружок, 26 любят спорт; 14 студентов посещают драмкружок и занимаются музыкой, 12 – занимаются музыкой и спортом, 7 – ходят в драмкружок и занимаются спортом, двое увлекаются всеми тремя занятий.
Пусть: I – множество студентов педфака;
А – множество студентов, которые увлекаются музыкой;
В – множество студентов, которые увлекаются спортом;
С – множество студентов, которые занимаются в драмкружке.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
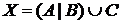 и
и 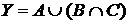
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько студентов занимаются спортом или музыкой?
22. Среди 78 натуральных чисел имеется: двузначных чисел – 28, 30 чисел – делятся на 3, 26 – делятся на 7; 14 двузначных чисел делятся на 3; 12 чисел делятся на 3 и на 7; 7 двузначных чисел делятся на 7; 20 чисел не являются двузначными и не делятся ни на 3, ни на 7.
Пусть: I – множество данных натуральных чисел;
А – множество двузначных чисел;
В – множество чисел, которые делятся на 3;
С – множество чисел, которые делятся на 7.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
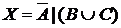 и
и 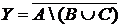
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько недвузначных чисел делятся на 3 или 7?
23. Среди 48 опрошенных студентов оказалось: 16 изучают английский язык, 24 – немецкий, 12 – французский; 8 студентов изучают английский и немецкий языки, 8 – французский и немецкий, 4 – французский и английский, причем двое из них не изучают немецкий.
Пусть: I – множество опрошенных студентов;
А – множество студентов, которые изучают английский язык;
В – множество студентов, которые изучают французский язык;
С – множество студентов, которые изучают немецкий язык.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
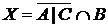 и
и 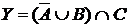
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько человек изучают только один язык?
24. Среди 100 геометрических фигур имеется: красных – 30, больших – 40; 10 – красных и больших, но не круглых; 12 – больших круглых, но не красных; 8 – красных и круглых, но не больших; 14 больших фигур не являются ни красными, ни круглыми; 20 фигур – не большие, не красные, не круглые.
Пусть: I – множество геометрических фигур;
А – множество красных фигур;
В – множество круглых фигур;
С – множество больших фигур.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
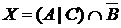 и
и 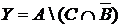
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько фигур являются красными или небольшими?
25. При опросе 110 человек оказалось: английский язык знают 44 человека, немецкий – 46, французский – 49, 13 человек владеют английским и немецким языками, 14 – немецким и французским, 15 – английским и французским; 8 человек не знают ни одного из этих иностранных языков.
Пусть: I – множество опрошенных людей;
А – множество людей, которые знают английский язык;
В – множество людей, которые знают французский язык;
С – множество людей, которые знают немецкий язык.
а) Отметьте штриховкой на диаграмме Эйлера–Венна множества
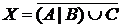 и
и 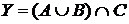
и сформулируйте характеристическое свойство элементов этих множеств.
б) В каком отношении находятся множества Х и Y ?
в) Сколько элементов содержат множества Х и Y ?
г) Сколько человек знают только два иностранных языка?
Связь между компонентами
Арифметических операций.
Решите уравнение, используя правила нахождения неизвестных компонент арифметических операций.
1. (420 : (160 – 1000 : х) + 24) × 5 = 180.
2. (((120 + х) × 40 : 2 + 200) : 131) : 20 = 1.
3. 1225 : ((13х - 30) × 4 : 12 – 10) = 7.
4. (10638 : х +2112 × 275 – 8597) : 6757 = 229.
5. 125125 : ((1001 – (1100х – 160) : 24) × 55) = 25.
6. 54756 : (51545 × (47859 – 47856х)) : 305) = 108.
7. 4 : ((48 – 5х) × 7 : 3 – 3) = 1.
8. ((87 – 24х) : 3 : 29 + 15) : 4 = 4.
9. ((3х – 54) × 8 – 159) : 21 = 21.
10. (((1835 + х) + 732545) : 937 – 375) × 412 = 168920.
11. ((239112 : (220 – х) + 1111) – 4432) × 398 = 0.
12.117 × (1056 : х + 12) : 195 + 40 = 100.
13. 7294545 : (45 × (х : 23 – 19500)) + 63 = 1000.
14. (420 : (160 – х : 8) + 24) × 5 = 180.
15. ((458 – х) : 2 – 112) × 18 + 6 = 1212.
16. ((25х + 200) : 30 – 88) × 50 – 86 = 14.
17. (((8х – 98) : 2 + 56) × 36 – 268) : 500 = 4.
18. ((12х + 1) × 20 + 200) : 131 – 19 = 1.
19. ((146 – 49х) : 2 + 156) × 16 – 635 = 2245.
20. ((11х + 98) : 3 – 37) × 15 + 69 = 279.
21. ((195х + 217) × 3 – 11) : 175 = 7.
22. 1335 : ((3189 – 3х) × 4 : 28 + 10) = 3.
23. ((15х + 1) × 60 : 2 – 200) : 104 = 20.
24. ((1154 – 7х) : 2 + 2398) : 11 – 159 = 107.
25. ((12563208 : х – 343581) × 3 + 809) : 17 = 1000.
Системы счисления.
Выполните действия в заданной системе счисления.
Сделайте проверку: переведите данные числа в десятичную систему счисления, выполните действия, переведите ответ в исходную систему счисления.
1. (13115 + 10105) : 4; 14. (2346 – 1456) × 146 ;
2. (23516 + 146 ) : 5 ; 15. (2232 4 : 3) – 124 ;
3. 5267 – (1507 : 6) ; 16. (25127 + 34137) : 3 ;
4. (2478 + 10138) × 358 ; 17. (40678 – 15258) : 5 ;
5. (101223 – 22123) ×1213 ; 18. (1159 + 1079) × 8 ;
6. (12467 : 5) + 1517 ; 19. 1213 + (102103 : 2);
7. (32017 + 2047) : 6 ; 20. (10536 – 2556) × 216 ;
8. (17149 – 7319) : 7 ; 21. (4135 + 12135) × 325 ;
9. (3326 + 5046) : 126 ; 22. (12167 – 1367) × 157 ;
10. (122034 – 30024):214 ; 23. (12334 + 1224) × 314 ;
11. (101110012 – 11001102) × 112 ; 24. (204315 × 115) : 225 ;
12. (15436 + 11446) × 216 ; 25. (33304 – 3234) × 134 ;
13. (15546 – 5356) × 1146 .
НОД и НОК чисел.
Вычислите НОД и НОК двух чисел двумя способами:
а) по каноническому разложению чисел;
б) с помощью алгоритма Евклида.
1. 1960 и 588; 14. 4620 и 7700;
2. 4608 и 24894; 15. 3072 и 2112;
3. 1980 и 720 16. 1320 и 9960;
4. 1995 и 1260; 17. 1155 и 5385;
5. 4608 и 774; 18. 8415 и 1515;
6. 1760 и 84700; 19. 84700 и 1430;
7. 13464 и 1644; 20. 1850 и 680;
8. 1530 и 1020; 21. 1875 и 29835;
9. 13464 и 6897; 22. 4326 и 13608;
10. 4628 и 8840; 23. 5720 и 139425;
11. 85800 и 7644; 24. 57596 и 24990;
12. 7888 и 7308; 25. 70785 и 172788.
13. 9405 и 18525.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
ПО МАТЕМАТИКЕ
Для студентов педагогического факультета
Могилев 2006
Пособие содержит задания по всем основным темам курса математики для педагогического факультета, по каждой теме – 25 вариантов.
Задания могут использоваться для составления контрольных работ, проведения зачетов, организации самостоятельной и индивидуальной работы студентов как заочного отделения, так и дневного.
С О Д Е Р Ж А Н И Е
| Номер задания | Т е м а | Стр. |
| 1. | Суждения и отношения между ними. | |
| 2. | Логическая функция и ее область истинности. | |
| 3. | Умозаключения, основанные на правилах логического следования. | |
| 4. | Операции над числовыми множествами. | |
| 5. | Разбиение множества на классы. Отношения между множествами | |
| 6. | Соответствие между множествами. Виды соответствий. | |
| 7. | Бинарное отношение на множестве. Свойства отношений. | |
| 8. | Теоретико-множественный смысл арифметических операций. | |
| 9. | Теоретико-множественное обоснование правил, связанных с операциями сложения и вычитания. | |
| 10. | Свойства арифметических операций. | |
| 11. | Связь между компонентами арифметических операций. | |
| 12. | Аксиоматический смысл арифметических операций. | |
| 13. | Метод математической индукции. | |
| 14. | Системы счисления. | |
| 15. | НОД и НОК целых неотрицательных чисел. | |
| 16. | Делимость целых неотрицательных чисел. | |
| 17. | Арифметические действия над действительными числами. | |
| 18. | Системы и совокупности неравенств с одной переменной. | |
| 19. | Системы уравнений с двумя переменными. | |
| 20. | Системы неравенств с двумя переменными. | |
| 21. | Свойства геометрических фигур (вычисления). | |
| 22. | Свойства геометрических фигур (доказательства). | |
| 23. | Геометрические преобразования (осевая симметрия). | |
| 24. | Геометрические преобразования (параллельный перенос, центральная симметрия). | |
| 25. | Геометрические преобразования (гомотетия, поворот). |
Суждения и отношения между ними
Два суждения заданы своими логическими формулами.
а) Установите отношения между этими суждениями.
б) Сформулируйте суждения, соответствующие этим формулам.
1. А Ú В Ú С и A Ú (Ø B É C)
2. Ø В ~ (Ø С Ú Ø А) и (Ø A É B) Ú (А É C)
3. А Ú В Ù С и A Ù Ø (B É C)
4. А Ù В Ù С и (A É Ø B) Ú C
5. Ø A Ù (B ~ C) и Ø А É В Ú С
6. Ø A Ú B É C и A É В Ù Ø С
7. A Ù (Ø B Ú Ø C) и A Ú (В ~ Ø С)
8. Ø A Ú (Ø B É Ø C) и Ø А Ù С ~ B
9. Ø A ~ Ø B Ú Ø C и В Ù С Ù Ø А
10. A É Ø (B Ù C) и А Ù С Ú Ø В
11. A Ù Ø B É Ø C и С ~ А Ú В
12. A Ú B É Ø C и Ø А É ØВ Ù С
13. Ø A Ù (Ø B ~ C) и Ø А Ú Ø(С É В)
14. Ø A É B Ù C и Ø С Ú А Ù В
15. A Ú (B É C) и Ø А Ù С É В
16. A É (B É C) и Ø (А Ù В) Ú С
17. A ~ B É C и А Ú Ø (В Ù Ø С)
18. A É B Ú C и А Ù (В ~ С)
19. С Ú Ø (А Ú В) и А Ù Ø В É Ø С
20. A Ú B ~ Ø C и Ø А Ù В É Ø С
21. Ø A Ù Ø B) Ú C и (Ø В ~ С) Ú А
22. Ø A &
