Разложение целого числа по степеням основания в различных системах счисления
Системы счисления.
Совокупность приемов наименования и записи чисел называется счислением. Под системой счисления понимается способ представления любого числа с помощью ограниченного алфавита символов, называемых цифрами. Счисление представляет собой частный случай кодирования, где слово, записанное с использованием определенного алфавита и по определенным правилам, называется кодом. Применительно к счислению это код числа.
Различают позиционные и непозиционные системы счисления. В непозиционных системах счисления каждое число обозначается соответствующей совокупностью символов. Характерным представителем непозиционных систем является римская система счисления со сложным способом записи чисел и громоздкими правилами выполнения арифметических операций.
Например запись МСМХСVIII означает, что записано число 1998 (М – тысяча, С – сто, Х – десять, V – пять, I – единица и т. д.).
Алфавит римской системы счисления:
G = { I, V, X, L, С , D, M }, где
I – единица (1),
V – пять (5),
X – десять (10),
L – пятьдесят (50),
С – сто (100),
D – пятьсот (500),
M – тысяча (1000).
Примеры:
IX = 9 XC = 90 CМ = 900
XI = 11 CX = 110 МC = 1100
VIII = 8 LXXX = 80 DCCC= 800
Позиционные системы счисления обладают большими преимуществами в наглядности представления чисел и в простоте выполнения арифметических операций.
В позиционной системе счисления значение числа определяется не только набором входящих в него цифр, но их местом (позицией) в последовательности цифр, изображающих это число, например, числа 127 и 721.
Позиционной является десятичная система счисления, используемая в повседневной жизни. Помимо десятичной существуют другие позиционные системы счисления, и некоторые из них нашли применение в информатике.
Количество символов, используемых в позиционной системе счисления, называется ее основанием. Его обозначают буквой q. В десятичной системе счисления используется десять символов (цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, и основанием системы является число десять. Все эти символы составляют алфавит системы счисления, который обозначается – G.
Особое место среди позиционных систем счисления занимают системы со степенными весами разрядов, в которых веса смежных позиций цифр (разрядов) отличаются по величине в постоянное количество раз, равное основанию q системы счисления.
В общем случае в такой позиционной системе счисления с основанием q любое число x может быть представлено в виде полинома разложения:
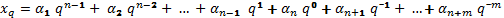, (1.1)
или в свернутом виде:
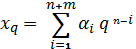
где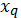 
– запись числа в системе счисления с основанием q;
q – основание системы счисления;
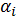– целые числа, меньше q;
n – число разрядов (позиций) в целой части числа;
m – число разрядов в дробной части числа.
Например:
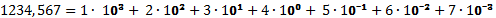
Для обозначения используемой системы счисления ее основание указывается в индексе. Изображение числа 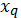в виде последовательности коэффициентов 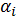полинома является его условной сокращенной записью (кодом).
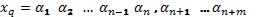, (1.2)
Запятая отделяет целую часть числа от дробной и служит началом отсчета значений веса каждой позиции (разряда).
В информатике применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную и шестнадцатеричную, то есть системы счисления с основанием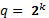 
, где k = 1, 3, 4.
Разложение целого числа по степеням основания в различных системах счисления
Десятичная система
Основание системы q = 10,
Алфавит системы G = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }, где все αi < 10
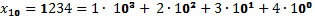
Длина числа n = 4
Разложение числа по степеням основания 10 в развернутой форме:
,
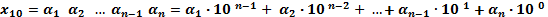или в свернутой форме:
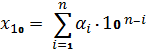
Двоичная система
Основание системы q = 2,
Алфавит системы G = {0, 1}, где все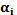 
< 2
;
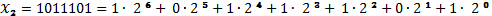Длина числа n = 7
Разложение числа по степеням основания 2 в развернутой форме:
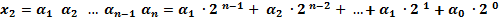
или в свернутой форме:
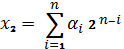
Восьмеричная система
Основание системы q = 8,
Алфавит системы G = {0, 1, 2, 3, 4, 5, 6, 7}, гдевсе 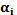< 8
;
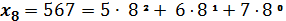Длина числа n = 3
Разложение числа по степеням основания 8 в развернутой форме:
,
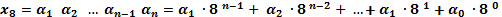или в свернутой форме:
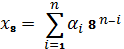
Шестнадцатеричная система
Основание системы q = 16,
Алфавит системы G = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,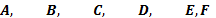 
}, где все 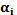< 16
=
;
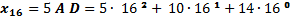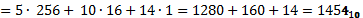Длина числа n = 3
Разложение числа по степеням основания 16 в развернутой форме:
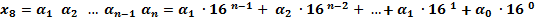
или в свернутой форме:
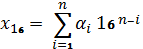
Преобразование чисел
ЭВМ работают с двоичными кодами, пользователю удобнее иметь делосдесятичными или шестнадцатеричными. Поэтому возникает необходимость перевода числа из одной системы счисления в другую.
Правило преобразование числа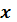 
из системы счисления с основанием p в систему счисления с основанием q осуществляется по правилу деления на основание системы счисления.
Реализуется на основании формулы (1.1) и предусматривает выполнение арифметических операций с кодами чисел в новой системе счисления. Поэтому оно чаще всего используется для преобразования чисел из недесятичной системы счисления в десятичную.
Правило деления используется для преобразования целого числа, записанного в p -ичной системе счисления, в q-ичную. В этом случае необходимо последовательно делить исходное p -ичное число и получаемые частные на новое основание q, представленное в p -ичной системе счисления. Деление продолжают до тех пор, пока очередное частное не станет меньше q. После замены полученных остатков ипоследнего частного цифрами q -ичной системы счисления записывается код числа в повои системе счисления. При этом старшей цифрой является последнее частное, а следующие за ней цифры соответствуют остаткам, записанным в последовательности, обратной их получению.