Показниковий закон розподілу часу обслуговування
Часом обслуговування називається час, витрачений кожним вузлом обслуговування на одну вимогу.
Час обслуговування характеризує пропускну здатність кожного вузла обслуговування, не пов’язаного з оцінкою якості обслуговування і є випадковою величиною.
Це пояснюється неідентичністю вузлів обслуговування і розходженням у попиті на обслуговування окремих вимог. Наприклад, вагони, що надійшли на ремонт, мають несправності різноманітного характеру, потрапляють у різні ремонтні бригади, тому час на обслуговування для різних вагонів буде різним.
У багатьох задачах теорії масового обслуговування закон розподілу часу обслуговування передбачається показовим і описується виразом
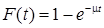 .
.
Параметр 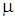 характеризує середню швидкість обслуговування вимог.
характеризує середню швидкість обслуговування вимог.
2.9 Завдання до самостійної роботи№1
1. Дано пуассонівський потік з параметром 2 хв-1. Знайти ймовірність того, що довжина інтервалу між сусідніми вимогами складає від однієї до двох хвилин.
2. Виконується накладення («суперпозиція») двох найпростіших потоків з інтенсивностями 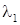 і
і 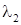 . Чи буде потік, що вийшов у результаті накладення, найпростішим, і якщо так, то з якою інтенсивністю?
. Чи буде потік, що вийшов у результаті накладення, найпростішим, і якщо так, то з якою інтенсивністю?
3. Виконується випадкове проріджування найпростішого потоку подій з інтенсивністю 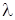 ; кожна подія, незалежно від інших, з ймовірністю p зберігається в потоці, а з ймовірністю 1-р викидається. Яким буде потік, отриманий у результаті проріджування найпростішого потоку?
; кожна подія, незалежно від інших, з ймовірністю p зберігається в потоці, а з ймовірністю 1-р викидається. Яким буде потік, отриманий у результаті проріджування найпростішого потоку?
4. Потік машин, що їдуть по шосе в одному напрямку, є найпростішим потоком з інтенсивністю 2 машини за хвилину. Людина виходить на шосе, щоб зупинити першу зустрічну машину, яка їде в даному напрямку. Знайти закон розподілу часу Т, протягом якого їй доведеться чекати машину; визначити математичне очікування і середнє квадратичне відхилення.
5. Потік машин, що їдуть по шосе в одному напрямку, є найпростішим потоком з інтенсивністю чотири машини за хвилину. Шосе має розгалуження в два напрямки. Ймовірність руху машин у першому напрямку дорівнює 0,12, а в другому – 0,88. Визначити інтенсивності руху автомобілів у обох напрямках.
6. Розглянемо найпростіший потік з нестаціонарним параметром, що змінюється по закону 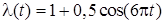 . Параметр є періодичним, його період дорівнює 1/3. Знайти ймовірність відсутності вимог на відрізку [1;9].
. Параметр є періодичним, його період дорівнює 1/3. Знайти ймовірність відсутності вимог на відрізку [1;9].
7. Комп'ютерний клас з’єднаний з каналом Інтернет через 10-канальний концентратор. Інтенсивності передачі даних по кожному з 10 каналів дорівнюють відповідно 540 біт/с, 120 біт/с, 40 біт/с, 170 біт/с, 350 біт/с, 60 біт/с, 742 біт/с, 153 біт/с, 500 біт/с, 100 біт/с. Потік даних підкоряється пуассонівському закону розподілу. Визначити інтенсивність передачі даних в каналі Інтернет.
8. Розглянемо найпростіший потік з нестаціонарним параметром, що змінюється за законом 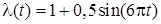 . Параметр є періодичним, його період дорівнює 1/4. Знайти ймовірність надходження однієї, двох і трьох вимог.
. Параметр є періодичним, його період дорівнює 1/4. Знайти ймовірність надходження однієї, двох і трьох вимог.
9. Для найпростішого потоку з нестаціонарним параметром, обумовленим рівністю 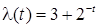 , знайти ймовірність надходження двох вимог на проміжку часу [3;8].
, знайти ймовірність надходження двох вимог на проміжку часу [3;8].
10. Залізницею повз спостерігача рухається в одному напрямку найпростіший потік потягів. Відомо, що ймовірність відсутності потягів протягом 10 хвилин дорівнює 0,8. Потрібно знайти ймовірність того, що за
20 хв повз спостерігача пройде не більше трьох потягів.
11. Виконується випадкове проріджування найпростішого потоку подій з інтенсивністю 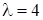 ; кожна подія, незалежно від інших, з ймовірністю p=0,6 зберігається в потоці, а з ймовірністю 1-р відкидається. Яким буде потік, отриманий в результаті проріджування найпростішого потоку?
; кожна подія, незалежно від інших, з ймовірністю p=0,6 зберігається в потоці, а з ймовірністю 1-р відкидається. Яким буде потік, отриманий в результаті проріджування найпростішого потоку?
12. Розглянемо найпростіший потік з нестаціонарним параметром, що змінюється за законом 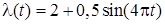 . Параметр є періодичним, його період дорівнює 1/3. Знайти ймовірність відсутності вимог на відрізку [1;5].
. Параметр є періодичним, його період дорівнює 1/3. Знайти ймовірність відсутності вимог на відрізку [1;5].
13. Дано пуассонівський потік з параметром 1 хв-1. Знайти ймовірність того, що довжина інтервалу між сусідніми вимогами складає від двох до чотирьох хвилин.
14. Потік машин, що їдуть по шосе в одному напрямку, є найпростішим потоком з інтенсивністю вісім машин за хвилину. Шосе має розгалуження в три напрямки. Ймовірність руху машин у першому напрямку дорівнює 0,12, у другому – 0,68, у третьому – 20. Визначити інтенсивності руху автомобілів у всіх напрямках.
15. Потік машин, що їдуть по шосе в одному напрямку, являє собою найпростіший потік з інтенсивністю 6 машин за хвилину. Людина виходить на шосе, щоб зупинити першу зустрічну машину, яка їде в даному напрямку. Знайти закон розподілу часу Т, який їй доведеться чекати; визначити його математичне очікування і середнє квадратичне відхилення.
16. Для найпростішого потоку з нестаціонарним параметром, обумовленим рівністю 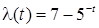 , знайти ймовірність надходження двох вимог на проміжку часу [1;10].
, знайти ймовірність надходження двох вимог на проміжку часу [1;10].
17. У пункт поточного ремонту вагонів надходять вимоги на ремонт. Потік вимог можна вважати найпростішим з інтенсивністю 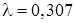 . Знайти ймовірність того, що за годину не надійде жодної вимоги (вагона) на ремонт.
. Знайти ймовірність того, що за годину не надійде жодної вимоги (вагона) на ремонт.
18. Час обслуговування для апаратів деякої системи масового обслуговування розподілено за показовим законом 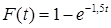 , де t –час у хвилинах. Знайти ймовірність того, що обслуговування триватиме не більше 15 хв.
, де t –час у хвилинах. Знайти ймовірність того, що обслуговування триватиме не більше 15 хв.
19. Для найпростішого потоку з нестаціонарним параметром, обумовленим рівністю 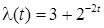 , знайти ймовірність надходження двох вимог на проміжку часу [2;6].
, знайти ймовірність надходження двох вимог на проміжку часу [2;6].
20. У пункт поточного ремонту вагонів надходить вимога на ремонт. Потік вимог можна вважати найпростішим з інтенсивністю 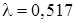 . Знайти імовірність того, що за годину надійде одна вимога (вагон) на ремонт.
. Знайти імовірність того, що за годину надійде одна вимога (вагон) на ремонт.
21. Час обслуговування для апаратів деякої системи масового обслуговування розподілено за показовим законом 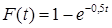 , де t – час у хвилинах. Знайти ймовірність того, що обслуговування триватиме не більше п’яти хвилин.
, де t – час у хвилинах. Знайти ймовірність того, що обслуговування триватиме не більше п’яти хвилин.
22. Виконується випадкове проріджування найпростішого потоку подій з інтенсивністю 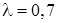 ; кожна подія, незалежно від інших, з імовірністю p=0,75 зберігається в потоці, а з імовірністю 1-р викидається. Яким буде потік, що виходить у результаті проріджування найпростішого потоку?
; кожна подія, незалежно від інших, з імовірністю p=0,75 зберігається в потоці, а з імовірністю 1-р викидається. Яким буде потік, що виходить у результаті проріджування найпростішого потоку?
23. Виконується розбиття випадкового найпростішого потоку подій з інтенсивністю 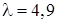 на три потоки. Імовірності влучення подій у той чи інший потік відповідно дорівнюють p1=0,2, p2=0,54, p3=0,26. Визначити інтенсивності кожного потоку, що вийшов у результаті розбиття.
на три потоки. Імовірності влучення подій у той чи інший потік відповідно дорівнюють p1=0,2, p2=0,54, p3=0,26. Визначити інтенсивності кожного потоку, що вийшов у результаті розбиття.
24. Час обслуговування для апаратів деякої системи масового обслуговування розподілено за показовим законом 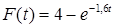 , де t – час у хвилинах. Знайти ймовірність того, що обслуговування триватиме не більше восьми хвилин.
, де t – час у хвилинах. Знайти ймовірність того, що обслуговування триватиме не більше восьми хвилин.
25. У пункт поточного ремонту вагонів надходять вимоги на ремонт. Потік вимог можна вважати найпростішим з інтенсивністю 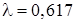 . Знайти імовірність того, що за годину надійде одна вимога (вагон) на ремонт.
. Знайти імовірність того, що за годину надійде одна вимога (вагон) на ремонт.
26. Виконується розбиття випадкового найпростішого потоку подій з інтенсивністю 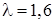 на два потоки. Імовірності влучення подій у той чи інший потік відповідно дорівнюють p1=0,44, p2=0,56. Визначити інтенсивності кожного отриманого в результаті розбиття потоку.
на два потоки. Імовірності влучення подій у той чи інший потік відповідно дорівнюють p1=0,44, p2=0,56. Визначити інтенсивності кожного отриманого в результаті розбиття потоку.
27. Комп'ютерний клас з’єднаний з каналом Інтернет через 5-канальний концентратор. Інтенсивності передачі даних по кожному з 10 каналів дорівнюють відповідно 541 біт/с, 110 біт/с, 44 біт/с, 171 біт/с, 356 біт/с. Потік даних підкоряються пуассонівському закону розподілу. Визначити інтенсивність передачі даних в каналі Інтернет.
28. Розглянемо найпростіший потік з нестаціонарним параметром, що змінюється за законом 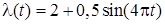 . Параметр є періодичним, його період дорівнює 1/3. Знайти імовірність відсутності вимог на відрізку [4;9].
. Параметр є періодичним, його період дорівнює 1/3. Знайти імовірність відсутності вимог на відрізку [4;9].
29. На вокзал прибуває пуассонівський потік потягів, у середньому два потяги за п’ять хвилин. Знайти імовірність того, що за 15 хвилин прибудуть три потяги.
30. Час обслуговування для апаратів деякої системи масового обслуговування розподілено за показовим законом 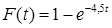 , де t – час у хвилинах. Знайти імовірність того, що обслуговування триватиме не більше
, де t – час у хвилинах. Знайти імовірність того, що обслуговування триватиме не більше
20 хвилин.
