Задача поиска. Красно-черные деревья. Задача балансировки для красно-черных деревьев.

Красно-черное дерево - это двоичное дерево поиска, обладающее следующими свойствами (будем называть их RB свойствами):

1. Каждый узел дерева покрашен либо в черный, либо в красный цвет.

2. Листьями объявляются NIL-узлы ("виртуальные" узлы, являющиеся сыновьями

узлов, которые в двоичном дереве поиска являлись листьями). Листья покрашены в

черный цвет.

3. Если узел красный, то оба его сына являются черными.

4. На всех ветвях дерева, ведущих от его корня к листьям, число черных узлов

одинаково.

Предыдущий пример в виде красно-черного дерева может быть представлен в следующем

виде:

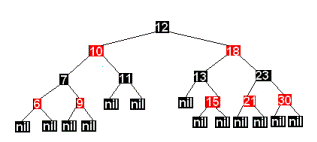
Количество черных узлов на ветви от корня до листа называется черной высотой дерева (по определению не зависит от выбранного листа). Перечисленные свойства гарантируют, что самая длинная ветвь, ведущая от корня к листу, не более чем в два раза длиннее любой другой ветви от корня к листу. Чтобы понять, почему это так, рассмотрим дерево с черной высотой h . Кратчайшее возможное расстояние от корня до листа равно h – когда все узлы черные. Самое длинное расстояние от корня до листа равно 2h , узлы при этом покрашены таким образом, что цвета чередуются (от корня к листу) так: красный, черный, красный, черный, …, красный, черный. Сюда нельзя добавить черные узлы, поскольку при этом нарушится свойство 4, из которого вытекает корректность понятия черной высоты. Поскольку согласно свойству 3 у красных узлов непременно черные наследники, в подобной последовательности недопустимы и два красных узла подряд. Таким образом, длиннейший путь, который мы можем сконструировать, состоит из чередования красных и черных узлов, что и приводит нас к удвоению длины пути, проходящего только через черные узлы. Поэтому можно считать, что красно-черное дерево поддерживает следующий критерий баланса: глубина любых двух листьев в дереве отличаются не более чем в два раза. Все операции над деревом используют и должны сохранять перечисленные свойства. В частности, эти свойства должны сохраняться при вставке и удалении. При соблюдении RB свойств, имеет место Лемма[4]. Красно-черное дерево с n внутренними вершинами (не считая NIL листьев) имеет высоту не более 2log(n +1) Наличие константы 2 перед логарифмом не сильно портит общего времени, необходимого на поиск, оно по прежнему составляет O(log n) , однако реализация операций балансировки на таком дереве попроще, чем в АВЛ деревьях. Рассмотрим операции вставки и удаления вершин дерева. Основная сложность анализа для этих операций заключается в том, что они могут испортить структуру красно-черного дерева, нарушив RB свойство. Операции вставки и удаления выполняются на красно-черном дереве за O(log n) шагов. Но эти операции могут нарушить RB свойства. Восстановление этих свойств требует перекраски некоторых вершин, а также выполнения операций вращения.

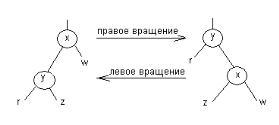
Каждая операция вращения требует O(1) времени. Операции левого и правого вращения являются обратными друг другу. При добавлении нового узла сначала ведется поиск места для этого узла в дереве. Добавленный листовой узел красится в красный цвет, его сыновья (NIL-узлы) окрашены в черные цвета. При вставке может быть нарушено RB- свойство 3, поскольку отец вставленной вершины также может быть окрашен в красный цвет. Если необходимо, мы перекрашиваем узел и производим поворот, чтобы сбалансировать дерево. Рассмотрим ситуацию, когда отец нового узла - красный: при этом будет нарушено свойство 3. Достаточно рассмотреть следующие два случая: Красный отец, красный "дядя": Ситуацию красный-красный иллюстрирует следующий рисунок.

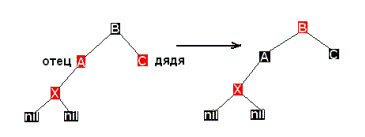
У нового узла X отец А и "дядя" С оказались красными. Простое перекрашивание избавляет нас от красно-красного нарушения. После перекраски нужно проверить "дедушку" нового узла (узел B), поскольку он может оказаться красным. Необходимо обратить внимание на распространение влияния красного узла на верхние узлы дерева. В самом конце корень красится в черный цвет. Если он был красным, то при этом увеличивается черная высота дерева Красный отец, черный "дядя": На рисунке ниже представлен другой вариант красно- красного нарушения - "дядя" нового узла оказался черным.

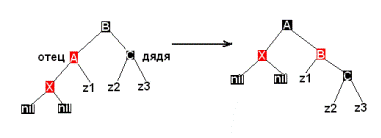
Здесь узлы может понадобиться вращать, чтобы скорректировать поддеревья. В этом месте алгоритм может остановиться из-за отсутствия красно-красных конфликтов и вершина дерева (узел A) окрашивается в черный цвет. Если узел X был в начале правым потомком, то первым применяется левое вращение, которое делает этот узел левым потомком. Рассмотрим наш пример: пусть вставляется элемент 5. Красно-черное дерево после вставки узла 5 выглядит следующим образом:

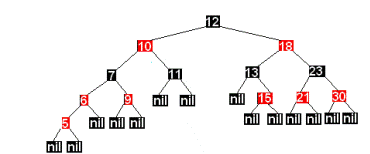
В этом дереве нарушено RB свойство 3(вершины 5,6). Используя первое преобразование, Получим

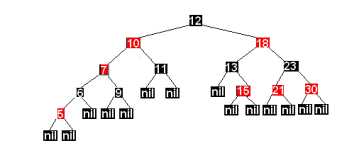
Поскольку для вершины 7 отец(10) и дядя(18) окрашены в красный цвет, то вновь используем преобразование 1.

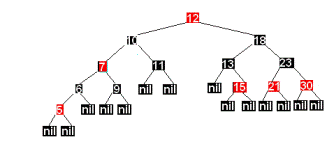
Последующее добавление 3 приведет к дереву

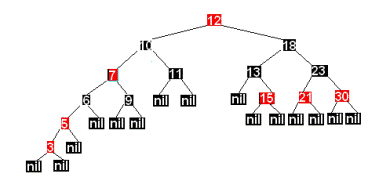
Однако ситуация с вершинами 3 и 5 несколько другая. Дядя вершины 3 имеет черный цвет. Применяя второе преобразование, получим

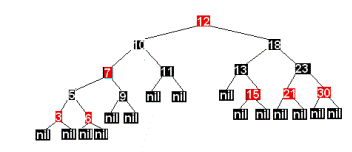
Метод удаления рассматривается аналогично .

Из-за сложности реализации операций балансировки считается, что сбалансированные деревья следует использовать лишь в том случае, когда операция поиска производится значительно чаще, чем включение. Можно предложить другую модель представления словаря, в которой все листья дерева расположены на одинаковом уровне, а степень ветвления вершин может быть более двух. Баланс в таких деревьях поддерживается за счет изменений степеней вершин. Наиболее простым примером такой структуры данных являются 2-3 деревья.