Метод изменения количества пробелов между словами выровненного по ширине текста

Данный метод позволяет скрывать данные в свободных местах текста, выровненного по ширине. При этом биты данных встраиваются путем управляемого выбора позиций, в которых будут размещены дополнительные пробелы. Один пробел между словами интерпретируется как "0". Два пробела — как "1". В среднем метод позволяет встраивать по несколько бит в одну строку.

Из-за ограничений, которые накладываются выравниванием текста по ширине, не каждый пробел между словами может использоваться для встраивания данных. Для возможности принятия однозначного решения при определении принимающей стороной, какие же именно из пробелов между словами скрывают встроенную информацию, а какие являются частью оригинального текста, в [14] предложено использовать метод встраивания, аналогичный манчестерскому кодированию.

В результате упомянутого кодирования биты группируются попарно, причем последовательность "01" интерпретируется как "1", "10" — как "0", а пары "00" и "11" считаются пустыми. Например, извлеченное сообщение "1010000111" сводится к "001", тогда как сообщение "0011110011" представляет пустую строку.

Приведем вариант реализации данного метода в программе MathCAD.

Шаг1

Примем, что пустой текстовый контейнер С и скрываемое сообщение М аналогичны использованным в двух вышерассмотренных методах.

Шаг 2

Встраивание сообщения в контейнер осуществляется с помощью программного модуля (M.133). Получение вектора двоичного представления скрываемого сообщения и подсчет количества символов в r-й текстовой строке выполняется аналогично тому, как это делалось в программном модуле (М. 131) (обозначено символом "#").

В процессе скрытия 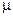-го бита сообщения вычисляются индексы i1 и i2, которые ограничивают r-ю текстовую строку в общем векторе С. В строку, которая имеет максимальное количество символов в своем составе (назовем ее длинной) — L_r = max(L), — данные не встраиваются. Во все остальные строки (назовем их короткими) — max(L)-L_r>0, — встраивание бит выполняется таким образом, чтобы добавление пробелов расширило текущую строку до размеров длинной строки.

Для выделенного из общего вектора С подмассива с, содержащего ASCII-коды символов короткой r-й строки, формируется массив space, размерность которого отвечает общему количеству пробелов t в данной строке, а каждые отдельные элементы содержат информацию о порядковом номере соответствующих им пробелов среди всех символов строки. Например, при r = 1, для контейнера, изображенного на рис. 5.94,

space^T =(7 14 18 25 39 42 48 56).

Из описания метода известно, что один бит данных встраивается в текстовый контейнер посредством модификации пары пробелов, которые заключают между собой одно слово предложения, путем добавления одного пробела в начале или в конце слова (в зависимости от значения скрываемого бита).Следовательно, количество бит Nb, которое можно встроить в r-ю строку, определяется соотношением между количеством возможных пар пробелов и количеством символов, на которое короткая строка "отстает" от длинной строки.

Если t/2 < max(L)-Lr, для встраивания бит можно использовать только floor(t/2)-1 пар пробелов; остальные будут использоваться для удлинения строки до размеров длинной путем создания пустых пар. При этом для упрощения алгоритма принимается, что извлечение на определенном участке строки пустой пары пробелов указывает на то, что в последующей части строки встроенных данных не содержится.

Если , для встраивания бит используется количество пар пробелов, которое равняется , поскольку именно этого количества символов не хватает короткой строке, чтобы сравняться по длине с длинной.

Так, например, для выбранного контейнера (рис. 5.94) длинной является шестая строка, которая содержит 70 символов. Первая строка является короткой: L₁ = 65. Для нее количество возможных пар пробелов t/2 = 8/2 = 4, что меньше чем 70-65 = 5. Таким образом, Nb = 3.

После определения количества пар пробелов, в которые могут быть встроены биты сообщения, из обрабатываемой строки выделяются сегменты , которые, соответственно, содержат 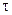-е пары пробелов. В нашем случае, для первой строки получаются следующие сегменты (для наглядности, изображены соответствующие ASCII-кодам символы):

Для каждого сегмента формируется вектор ssp, состоящий из двух элементов, каждый из которых содержит индекс соответствующего ему пробела. Например, для отмеченных выше сегментов:

С помощью дополнительно определенной функции ins_vec2vec( 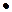) (программный модуль (M.134)) формируются новые сегменты, в которых добавлен один пробел либо к первому, либо ко второму пробелу — в зависимости от значения текущего встраиваемого бита.

В общей сложности, функция ins_vec2vec(A, В, 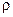) позволяет проводить встраивание вектора В в вектор А, начиная с позиции .

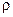В нашем применении в качестве вектора, в который происходит встраивание, выступает сегмент . При этом ASCII-код пробела (В = 32) встраивается после первого ,если M_vec__bin=1. или же после второго , если M_vec__bin=0,пробела сегмента.

В частности, для приведенных выше сегментов получаются следующие модифицированные сегменты (напомним, что первым встраивается символ "А", код которого в двоичном эквиваленте — D2B(str2vec("A"))^T = (0_LSB 0 0 0 0 0 1 1_MSB), а встраивание проводится, начиная с наименее значащих бит):

Полученные новые сегменты формируют r-ю строку стеганограммы (s_r). После встраивания последнего (Nb-гo) разрешенного в данной строке бита и формирования начала строки s_r, возможен случай, когда остается сегмент ориги

нальной строки с, который не претерпел модификации — seg_end. Для первой строки, например,

Если t/2<max(L)-L_r, к первым двум пробелам данного завершающего сегмента прибавляются еще по пробелу, что позволит после присоединения этого сегмента к уже полученной части строки s_r получить строку, количество символов в которой будет равняться max(L). Если же выполняется условие , завершающий сегмент не изменяется.

Для рассматриваемого выше примера, последний сегмент претерпевает модификацию, после которой приобретает следующий вид:

Как уже было отмечено, вне зависимости от того, был или не был модифицирован завершающий сегмент, он дописывается в конец r-й строки стеганограммы.

На заключительном этапе полученные строки s стеганограммы объединяются в общий массив S.

Параллельно, в программном модуле (M.133) проводится подсчет количества символов обработанных строк 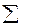. Это позволяет определить индекс символа оригинального текста, после которого текст не претерпел изменений (например, по причине того, что скрываемое сообщение закончилось до того момента, как был достигнут конец текста), и дописать немодифицированный текст в конец полученной стеганограммы.

Фрагмент результата встраивания сообщения Мв текстовый контейнер С приведен на рис. 5.97.

Рис. 5.97. Фрагмент текстового контейнера, заполненного методом изменении количества пробелов между словами выровненного по ширине текста

Нетрудно заметить, что в данном фрагменте скрыто 24 бита сообщения, что отвечает его первым трем символам ("Алг"). В частности, в 1-й строке скрыто биты 000, во 2-й — 00, в 3-й — 0, в 4-й — 11 (имеем символ "А"), в 5-й — 11, в 6-й — ни одного бита, в 7-й — 010, в 8-й — 111 (имеем символ "л"), в 9-й — 110, в 10-й — 0011, и, наконец, в 11-й — 1 (имеем символ "г").

Шаг 3

Извлечение из контейнера S*:= S встроенных в него бит информации осуществляется с помощью программного модуля (М.135), представленного ниже.

В начале модуля выполняется подсчет количества символов в каждой из строк текста S*. Используя полученный при этом массив L, вычисляются индексы i1 и i2, которые ограничивают r-ю текстовую строку в общем векторе S*.

Для выделенной из вектора S* строки-подмассива s формируется вектор space, размерность которого отвечает общему количеству пробелов в данной строке, а элементы содержат информацию о порядковых номерах соответствующих им пробелов среди всего множества символов строки.

На основе полученного вектора space формируется вектор b, значение каждого элемента которого зависит от результата вычисления разности между следующим и текущим значениями элементов вектора space. Если указанная разность равняется единице, элемент b_jпринимает значение 1, Если же значение разности превышает единицу, то элементу b_jприсваивается значение 0.

Из полученного вектора b выделяются подмассивы, состоящие из трех элементов (так называемые трибиты), на основе которых делается вывод о текущем значении встроенного бита: если трибит представляет собой последовательность (0 1 0), то извлекаемый бит — "0"; если же (1 0 0), извлекаемый бит — "1". Во всех других случаях принимается решение об отсутствии встроенных бит.

Сформированная таким образом двоичная последовательность преобразовывается в строку символьных данных, которая и возвращается переменной М*.

Рассмотренные методы произвольного интервала эффективны, при условии, что текст представлен в формате ASCII. Как было уже отмечено выше, некоторые данные могут оказаться утраченными после распечатывания текста. Печатные документы выдвигают к скрытию данных такие требования, которые далеко выходят за возможности текстового файла при кодировании ASCII. При этом скрытие данных в "жестких" копиях текста может выполняться путем незначительных изменений расстояния между словами и отдельными буквами, изменением позиций базовых линий (линий, на которых лежат наиболее низкие элементы букв или знаков пунктуации строки), изменением форм символов и т.п.