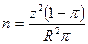Метод доверительных интервалов

Определение объема выборки методом доверительных интервалов основано на их создании вокруг выборочного среднего или выборочной доли с использованием формулы стандартной ошибки. В качестве примера предположим, что исследователь провел простую случайную вы­борку из 300 семей, чтобы оценить ежемесячные расходы семьи на покупки в универмаге, и определил, что средний ежемесячный расход семьи в выборке равен 182 доллара. Предыдущие исследования показали, что среднеквадратичное отклонение расходов в исследуемой совокуп­ности равно 55 долларов.

Мы хотим найти интервал, в который попадал бы определенный процент выборочных средних. Предположим, мы хотим определить интервал вокруг среднего значения совокуп­ности, который включал бы 95% выборочных средних, опираясь на выборку из 300 семей. 95% выборочных средних можно разделить на две равные части, половина меньше и поло­вина больше среднего, как показано на рис. 12.1. Вычисление доверительного интервала включает определение области меньше ( 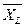) и больше ( 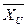) среднего значения ( 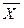) величины расходов.

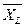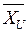Значения z, соответствующие и , можно рассчитать следующим образом:

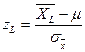
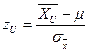
где Z_L= -Z и Zu = +Z . Следовательно, минимальное значение 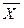определяется как 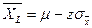, а максимальное значение 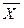равно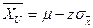

Доверительный интервал устанавливается как .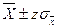

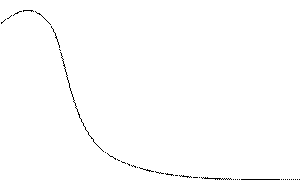
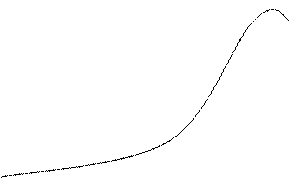
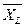
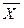
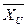
Рис 12.1. 95%-ный доверительный интервал

Теперь установим 95%-ный доверительный интервал вокруг выборочного среднего, равно­го 182 доллара. Для начала мы вычислим стандартную ошибку среднего:

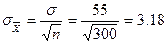
Из табл. 2 Приложения "Статистические таблицы" видно, что центральные 95% нормаль­ного распределения находятся в пределах ±1,96 значений z; 95%-ный доверительный интервал определяется как

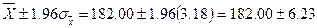
Таким образом, 95%-ный доверительный интервал находится в пределах от 175,77 до 188,23 доллара. Вероятность нахождения истинного среднего значения наблюдаемой совокупности в пределах от 175,77 до 188,23 доллара составляет 95%.

Определение объема выборки: среднее

Метод, использованный для создания доверительного интервала, можно модифицировать так, чтобы определить объем выборки с учетом желательного доверительного интервала [5]. Предположим, что вы хотите рассчитать ежемесячный расход семьи на покупки в универмаге более точно, так, чтобы полученный результат находился в пределах ±5,00 долларов от истин­ного среднего значения исследуемой совокупности. Каким должен быть объем выборки? В табл. 12.2 приведен необходимый перечень действий, который вы должны выполнить.

1. Определите степень точности. Это максимально допустимое различие (D) между выбороч­ным средним и генеральным средним. В нашем примере D = ±5,00 долларов.

2. Укажите уровень достоверности. Предположим, что желательный уровень достоверности 95%.

3. Определите значение z, связанное с данным уровнем достоверности, воспользовавшись табл. 2 в Приложении "Статистические таблицы". При 95%-ном уровне достоверности ве­роятность того, что среднее значение генеральной совокупности выйдет за пределы одно­стороннего интервала, равна 0,025 (0,05/2). Соответствующее значение z составляет 1,96.

4. Определите стандартное отклонение среднего генеральной совокупности. Его можно получить из вторичных источников или рассчитать, проведя пилотное исследование. Кроме того, стандартное отклонение можно установить на основе мнения исследователя. Например, диапазон нормально распределенной переменной примерно укладывается в шесть стандартных отклонений (по три слева и справа от среднего значения). Таким образом, можно рассчитать среднеквадратичное от­клонение, разделив величину всего диапазона на 6. Исследователь часто может определить раз­меры диапазон, исходя из собственного понимания анализируемых явлений.

5. Определите объем выборки, воспользовавшись формулой стандартной ошибки среднего:

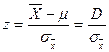
или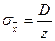

или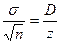

или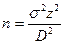

В нашем примере

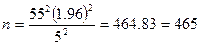(округленное в большую сторону до ближайшего целого числа).

Таблица 12.2. Определение объема выборки с помощью среднего и доли
	Этапы	Средние	Доли
	Установите степень точности	D = ±5,00 долл.	D = p-n =±0,05
	Укажите уровень достоверности (УД)	УД = 95%	УД = 95%
	Определите значение z, связанное с УД	Значение z= 1,96	Значение z= 1,96
	Определите стандартное отклонение сред­него генеральной совокупности	Определите σ σ = 55	Определите π π = 0,64
	Определите объем выборки с помощью формулы стандартной ошибки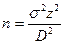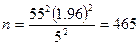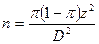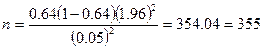
	Если объем выборки составляет 10% от объема популяции, примените окончатель­ную коррекцию совокупности (fpc)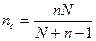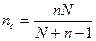
	При необходимости пересчитайте величину доверительного интервала, применив s для расчета σ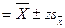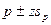
	Если степень точности указана в относительных, а не абсолютных показателях, воспользуйтесь данными уравнениями для определения объема выборки	D=Rµ	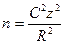D=Rπ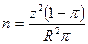

Из формулы объема выборки видно, что она растет с ростом изменчивости генеральной со­вокупности, а также с увеличением уровня достоверности и степени точности, с которой должны проводиться расчеты. Объем выборки прямо пропорционален σ ², поэтому, чем больше показатель изменчивости генеральной совокупности, тем больше объем выборки. Аналогично, более высокий уровень достоверности предполагает большее значение z и, следовательно, больший объем выборки. Переменные σ ² и z находятся в числителе. Увели­чение степени точности достигается уменьшением значения D и, следовательно, увеличи­вает объем выборки, поскольку D находится в знаменателе.

6. Если объем выборки составляет 10% и больше от объема генеральной совокупности, то применяется окончательная коррекция совокупности (fpc). Затем необходимый объем вы­борки рассчитывается по формуле

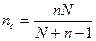
где п — объем выборки до применения окончательной коррекции;

п_с — объем выборки после применения окончательной коррекции.

7. Если среднеквадратичное отклонение совокупности σ неизвестно и используется его пред­положительное значение, то его следует повторно рассчитать после получения выборки. Среднеквадратичное отклонение выборки s используется в качестве предположительного значения σ. Затем следует вычислить исправленный доверительный интервал, чтобы опре­делить фактически полученную степень точности.

Предположим, что значение 55,00 использовалось в качестве предположительного значе­ния σ, потому что истинное значение было неизвестно. Получена выборка, в которой п = 465. На основе данных исследования рассчитывается среднее 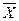, равное 180,00, и среднеквадратичное отклонение выборки 5, равное 50,00. Тогда исправленный доверительный интервал составит

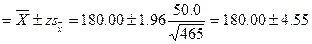
или

175, 45 ≤µ≤ 184,55

Обратите внимание, что полученный доверительный интервал уже предполагаемого. Это вызвано тем, что среднеквадратичное отклонение совокупности завышено на основании выборочных характеристик.

8. Иногда точность определена в относительных, а не абсолютных показателях. Другими сло­вами, может быть известно, что результат вычисления должен составить плюс-минус R% от среднего. Это означает, что D = Rµ.

В этом случае объем выборки можно определить как

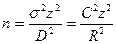
где нужно рассчитать коэффициент вариации С = (σ /µ).

Объем генеральной совокупности N не влияет на объем выборки напрямую, за исключением случаев, когда применяется коэффициент окончательной коррекции совокупности. Возможно, это кажется невероятным, но если подумать, в этом утверждении есть смысл. Например, если ис­следуемые характеристики всех элементов совокупности идентичны, то выборки, состоящей из одного элемента, вполне достаточно, чтобы рассчитать среднее. Это также правильно, если совокупность состоит из 50, 500, 5000 или 50000 элементов. В то же время изменчивость характеристик совокупности напрямую влияет на объем выборки. Эта изменчивость учитывается при вычисле­нии объема выборки с помощью дисперсии совокупности σ² или дисперсии выборки s².

Определение объема выборки: доля

Если изучаемая статистика является не средним, а долей, то маркетолог определяет объем вы­борки аналогичным образом. Предположим, что исследователя интересует установление доли се­мей, владеющих кредитной карточкой универмага. Порядок действий будет следующим [6].

1. Укажите степень точности. Предположим, желательная степень точности такова, что допус­тимый интервал установлен на уровне D = р – π= ±0,05.

2. Укажите уровень достоверности. Предположим, что желателен 95%-ный уровень достоверности.

3. Определите значение z, связанное с данным уровнем достоверности. Как объяснялось при расчете среднего, оно составит z = 1,96.

4. Определите генеральную долю я. Как мы указывали раньше, ее можно получить из вторич­ных источников, в ходе экспериментального исследования или на основе мнения исследо­вателя. Предположим, что на основе вторичных данных исследователь делает предположе­ние, что 64% семей из изучаемой генеральной совокупности обладают кредитной карточкой универмага. Следовательно, π= 0,64.

5. Определите объем выборки с помощью формулы стандартной ошибки доли:

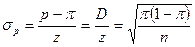
или

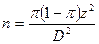
В нашем примере

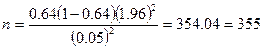(округленное в большую сторону до целого числа)

6. Если конечный объем выборки составляет 10% и больше от объема совокупности, приме­няется окончательная коррекция совокупности (fpc). Затем необходимый объем выборки рассчитывается по формуле

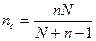
где

п — объем выборки до применения окончательной коррекции;

п_с — объем выборки после применения окончательной коррекции.

7. Если расчет π был неверным, то доверительный интервал будет более или менее точным, чем необходимо. Предположим, что по окончании выборки рассчитывается значение доли p, равное 0,55. Затем повторно вычисляется доверительный интервал, при этом s_p использу­ется для расчета неизвестного σ_р, а именно

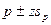
где

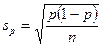
В нашем случае

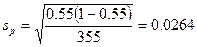
Доверительный интервал тогда равен 0,55 ± 1,96 (0,0264) = 0,55 ± 0,052, что означает, что он шире, чем было задано. Это объясняется тем, что среднеквадратичное отклонение вы­борки при р = 0,55 оказалось большим, чем предположительное значение среднеквадратич­ного отклонения совокупности, при π = 0,64.

Если интервал, превышающий указанный, недопустим, объем выборки можно скорректи­ровать так, чтобы отразить максимально возможное отклонение в совокупности. Такое от­клонение происходит, когда произведение π (1 — π) достигает максимального значения, для чего π должно равняться 0,5. К этому выводу можно прийти и без расчетов. Поскольку у одной половины совокупности одно значение характеристики, а у другой — другое, потре­буется больше данных, чтобы сделать правильный вывод, нежели когда ситуация более четко определена, и у большинства элементов одно значение характеристики. В нашем примере это приведет к получению объема выборки, равного

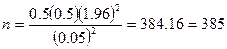(округлено в большую сторону до целого числа).

8. Иногда точность определена в относительных, а не абсолютных показателях. Другими сло­вами, может быть известно, что результат вычисления должен составить плюс-минус R% от доли совокупности. Это означает, что D = R π .

В этом случае объем выборки можно определить как