Перевод чисел из одной позиционной системы счисления в другую

Лабораторная работа №121.

Цель работы.Изучение методов и отработка навыков перевода чисел из одной позиционной системы счисления в другую.

Количество различных цифр 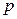, используемых в позиционной системе, определяет название системы счисления и называется основанием 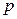-ой системы счисления.

Любое число N в позиционной системе счисления с основанием 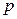может быть представлено в виде полинома от основания :

,

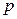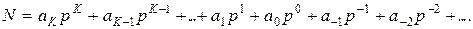где 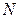— число, 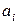— цифры числа (коэффициенты при степенях 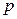), 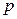— основание системы счисления ( 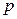>1).

Числа записывают в виде последовательности цифр:

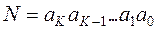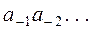. , точка в последовательности отделяет целую часть числа от дробной (коэффициенты при неотрицательных степенях, от коэффициентов при отрицательных степенях). Точка опускается, если число целое (нет отрицательных степеней).

В компьютерных системах применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.

В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из которых обозначается 0, а другое — 1. Поэтому арифметико-логической основной ЭВМ является двоичная система счисления.

Двоичная система счисления. Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в ви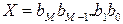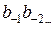де: . , где 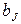либо 0, либо 1.

Эта запись соответствует сумме степеней числа 2, взятых с указанными коэффициентами:

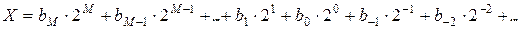
Восьмеричная система счисления.Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (см. таблицу 1).

Шестнадцатеричная система счисления. Для изображения чисел используется 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр — латинскими буквами: A (10), В (11), C (12), D (13), E (14), F (15). Шестнадцатеричная система, так же как и восьмеричная, используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (см. табл. 1).

Таблица 1.

Алфавиты позиционных систем счисления (сс)

Двоичная сс (Основание 2)	Восьмеричная сс (Основание 8)	Десятичная сс (Основание 10)	Шестнадцатеричная сс (Основание 16)
		Двоичные триады			Двоичные тетрады
				A (10) B (11) C(12) D(13) E(14) F(15)

Задание 1.Переведите числа из заданных систем счисления в десятичную систему.