Усеченное нормальное распределение

При нормальном (гауссовом) распределении случайной величины ось абсцисс имеет протяженность от –¥ до +¥. Поскольку время t не мо­жет быть отрицательной величиной, в теории надежности используется усеченное нормальное распределение.

Усеченным нормальным распределением случайной величины назы­вается распределение, получаемое из нормального при ограничении интер­вала возможных значений этой величины.

Основными параметрами для нормального распределения являются: Т – среднее значение наработки на отказ, s_t – среднеквадратическое откло­нение:

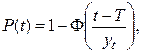(2.17)

где 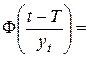Ф(и) – нормированная функция нормального распределе­ния. Значения Ф(и) приведены в литературе. При этом Ф(–и) = 1 – Ф(и),

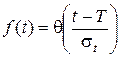. (2.18)

Значения q(и) приведены в литературе. При этом q(–и) = q(и),

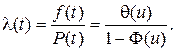(2.19)

Примерный вид соответствующих кривых представлен на рис. 2.3.

Нормальное распределение может использоваться при исследовании надежности объектов, отказы которых обусловлены действием какого-то одного доминирующего фактора.

Пример 2.3.Пусть параметры нормального распределения Т = 100 ч, 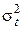= 1000 ч². Найти Р(70), Q(70), l(70), P(130), Q(130), l(130). Из формул (2.17)–(2.19):

Р(70) = 1 – Ф 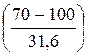= 1 – Ф(–0,95) = Ф(0,95) = 0,829,

Q(70) = 1 – Р(70) = 0,171,

l (70) = 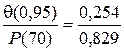= 0,306,

Р(130) = 1 – Ф 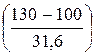= 1 – Ф(0,95) = 0,171,

Q(130) = 1 – Р(130) = 0,829,

l(130) = 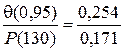= 1,485.