Замкнуті системи масового обслуговування
У замкнутих системах масового обслуговування джерело вимог знаходиться всередині системи, і інтенсивність потоку вимог залежить від стану самої системи.
Найчастіше потоком вимог у такій системі є потік несправностей від деякої групи працюючих приладів. Нехай є m працюючих приладів, які можуть виходити із робочого стану за рахунок несправностей. Є також N приладів (каналів) обслуговуючих ці вимоги. Такими каналами можуть виступати і люди. Звичайно вважають, що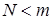 
.
Позначимо через S0 стан, при якому всі прилади працюють, а прилади обслуговування незайняті; S1 – стан, при якому один прилад вийшов із робочого стану і обслуговується одним приладом обслуговування; SN – N приладів не працюють і всі прилади зайняті обслуговуванням; Sm – всі прилади не працюють, із них N обслуговуються і m – N чекають обслуговування.
Ймовірність станів замкнутої системи визначається такими залежностями:
,
,
.
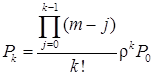
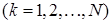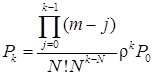
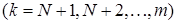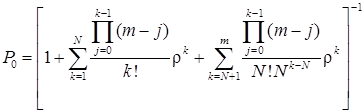Середня довжина черги:
.
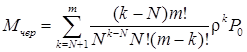Коефіцієнт простою вимог в СМО:
.
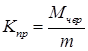Середня кількість вимог в СМО:
,
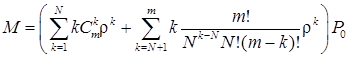де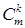 
– коефіцієнт бінома Ньютона.
Середня кількість вільних каналів і коефіцієнт простою каналів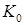 
:
; 
.
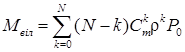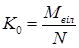Ймовірність зайнятості каналів обслуговування:
.
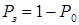Абсолютна пропускна здатність:
.
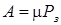Приклад. Робітник обслуговує групу із трьох станків. Кожний станок зупиняється в середньому два рази за годину. Процес налагоджування займає в середньому 10 хв. Визначити абсолютну пропускну здатність налагоджування робочих станків.
Маємо: n=1, m=3, l=2, Тобс=1/6, m=6. Знаходимо: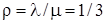 
,
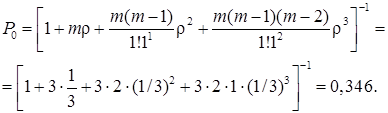
Визначаємо ймовірність того, що робітник буде зайнятий обслуговуванням:
.
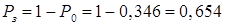Якщо робітник зайнятий обслуговуванням, то він обслуговує шість станків за годину. Отже, абсолютна здатність знаходиться як добуток:
.
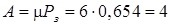Тобто А=4 станки за годину.
3.8 Завдання до самостійної роботи №2
1. У довідковій службі вокзалу залізничної дороги стоїть телефон з п’ятьма каналами. Вхідний виклик отримує відмову тоді, коли всі канали зайняті. Нехай середній час зайнятості одного каналу – 1 хвилина. Інтенсивність вхідних викликів становить 0,1 хв-1. Потрібно знайти ймовірність відмови і відносну пропускну здатність.
2. На залізничній станції знаходиться три каси для продажу квитків на потяги далекого слідування. Коли всі каси зайняті, пасажири стають в чергу. Довжина черги не може перевищувати 50 осіб. Середній час обслуговування в одній касі – 5 хвилин. Пасажири прибувають на станцію для купівлі квитків в середньому по дві людини за хвилину. Знайти ймовірність відмови і загальну кількість людей (вимог), які знаходяться в системі.
3. Для умови задачі 1 знайти ймовірність обслуговування виклику, а також ймовірність надходження одного виклику.
4. На залізничній станції маємо п’ять колій для обслуговування залізничних потягів, що прибули. Інтенсивність прибуття залізничних потягів дорівнює 15 потягів за годину. Середній час обслуговування одного потяга
20 хвилин. Вважають, що черга очікування обслуговування потягів може бути необмеженої довжини. Знайти ймовірність зайнятості всіх п’яти колій залізничної станції, середній час обслуговування потяга.
5. Програміст обслуговує комп’ютерний центр із 50 комп’ютерів.
У середньому комп’ютер дає збій 0,05 годин-1. Процес налагодження займає в середньому 45 хвилин. Визначити абсолютну пропускну здатність налагодження комп’ютерів програмістом.
6. У локомотивному депо обслуговується 100000 залізничних вагонів. Кожен вагон в середньому ремонтується один раз у два роки. На ремонт вагона затрачається в середньому 5 днів. Знайти ймовірність того, що депо зайнято обслуговуванням вагонів.
7. Сервіс-центр займається посередницькою діяльністю з продажу залізничних квитків і здійснює частину своєї діяльності по трьох телефонних лініях. В середньому в сервіс-центр надходить 75 дзвінків за годину. Середня тривалість обслуговування кожного дзвінка – 2 хвилини. Визначити ймовірність того, що жоден канал не зайнятий, а також ймовірність відмови.
8. Викладач приймає екзамен у групи студентів із 23-х осіб, які прийшли протягом однієї хвилини. Час прийняття екзамену у одного студента в середньому – 20 хв. Студенти, що очікують здачу екзамену, знаходяться в черзі. Визначити середню тривалість очікування студентів здачі екзамену.
9. Для умови задачі 7 визначити ймовірність зайнятості одного і двох каналів телефонної лінії.
10. У вагоні-ресторані інтенсивність обслуговування клієнтів у середньому – 20 осіб за годину. Обслуговує клієнтів два офіціанти, при цьому середня тривалість обслуговування одного клієнта – 10 хвилин. Середня кількість клієнтів, що залишили чергу, не дочекавшись обслуговування, становить дві особи за годину. Визначити абсолютну пропускну здатність вагону-ресторану.
11. Для умови задачі 7 визначити абсолютну пропускну здатність сервісного центра.
12. В читальний зал національної бібліотеки, яка має 30 місць, приходять відвідувачі з інтенсивністю 20 осіб за годину. Тривалість прибуття кожного відвідувача в середньому складає дві години. Визначити ймовірність відмови відвідувачу в читальному залі і середню кількість зайнятих місць.
13. Абонентський відділ бібліотеки обслуговує три бібліотекаря. Тривалість обслуговування одним бібліотекарем читача в середньому складає 5 хвилин. Інтенсивність відвідування читачами бібліотеки складає чотири особи за хвилину. Якщо в момент приходу читача всі бібліотекарі зайняті, то він стає в чергу. Потрібно визначити середню кількість читачів, які чекають початку обслуговування і час їх перебування в черзі.
14. Потік завдань в чотирипроцесорному комп’ютері є найпростішим з інтенсивністю 1000 завдань за хвилину. Середній час виконання завдання кожним процесором – три секунди. Якщо при надходженні завдання всі процесори зайняті, то завдання переміщається в чергу (черга необмежена). Потрібно визначити середню довжину черги і середню кількість зайнятих процесорів.
15. У комп’ютерному класі установлений один принтер, швидкість друку якого в середньому – дві сторінки за хвилину. Друк починається відразу після надходження файлу на порт принтера. Середня тривалість між надходженнями файлів на принтер одна хвилина. Якщо в момент надходження файла на друк принтер зайнятий, то завдання розміщуються в необмежену чергу. Потрібно визначити середню довжину черги і загальну тривалість перебування файлів в черзі, якщо кожний файл в середньому містить п’ять сторінок.
16. На базу даних (БД) сервера залізничної дороги надходить 10 запитів в секунду. Середній час обробки кожного запиту одна секунда. Запит, який надходить в момент обробки попереднього запита, стає в чергу. Визначити ймовірність наявності черги і сумарний час, який проведуть запити до обслуговування.
17. На залізничній станції розташований готель, в якому є 20 місць.
У разі відсутності місць відвідувач переходить у інший готель. Середня тривалість проживання клієнта в готелі 8 годин. Інтенсивність потоку надходження клієнтів складає 5 осіб за годину. Визначити ймовірність відмови і абсолютну пропускну здатність даного готелю.
18. На телефонній станції залізничної дороги є три лінії. Виклик, який поступає, коли всі лінії зайняті, отримує відмову. Потік викликів є пуассонівським з інтенсивністю 0,5 викликів на хвилину. Тривалість обслуговування розподілено за експонентним законом і в середньому тривалість розмови складає три хвилини. Знайти ймовірність відмови, відносну і абсолютну пропускні здатності і долі вільного часу, які приходяться в середньому на кожну лінію.
19. Чотириканальний концентратор має буфер ємністю 10 Мб. Пакети даних надходять на концентратор з інтенсивністю 51 пакет у секунду. Пакети, що надійшли в момент, коли зайняті всі канали, стають в чергу в буфері обміну, якщо він зайнятий – одержують відмову. Середня швидкість одного каналу
256 Кб в секунду. Визначити абсолютну пропускну здатність каналу концентратора при середньому розмірі пакета два Кб.
20. Два робітники обслуговують групу із чотирьох верстатів. Зупинка робочого верстата відбувається в середньому через 30 хвилин. Час роботи й час налагодження розподілений за експонентним законом. Знайти середню частку вільного часу для кожного робітника й середній час роботи верстата.
21. Для умови завдання 19 визначити ймовірність відмови передачі пакета й середню кількість вільних каналів концентратора, якщо середній розмір повідомлення – 5 Кб.
22. Розглянемо приклад про дві поряд розташовані телефонні кабіни, загальна черга перед якими не буває більше трьох осіб («інші» йдуть до інших кабін). Потік людей, що бажають зателефонувати, є найпростішим і має інтенсивність 15 осіб за годину. Час, проведений ними в кабіні, розподілено за експонентним законом і складає в середньому три хвилини. Знайти середню частку часу, коли вільна одна кабіна; ймовірність того, що особа піде шукати іншу кабіну.
23. Для умови завдання 20 знайти задані характеристики системи, у якій два робітники завжди обслуговують верстат разом, причому з подвійною інтенсивністю.
24. У буфеті залізничної станції обслуговують клієнтів два продавці. Інтенсивність обслуговування одним продавцем складає 0,5 особи за хвилину. Відвідувачі приходять у буфет із середнім інтервалом в 1 хвилину. Якщо в момент приходу клієнта всі продавці зайняті, клієнт стає в чергу, що не може перевищувати п’ять осіб. Відвідувач, що не потрапив у чергу, іде в інший буфет. Визначити ймовірність відмови відвідувачеві в обслуговуванні і середній час очікування в черзі.
25. Залізничний пропускний митний пункт складається із трьох ліній огляду. Час огляду одного поїзда на лінії огляду в середньому складає чотири години. Інтенсивність потягів, що прибувають, складає два потяги на годину. У випадку зайнятості всіх ліній огляду прибулий потяг ставиться на запасний шлях. Визначити абсолютну пропускну здатність митного пункту й середній час простою ліній огляду.
26. Залізнична сортувальна гірка, на яку подається найпростіший потік потягів з інтенсивністю два потяги на годину, є СМО з необмеженою чергою. Час обслуговування (розпуску) потяга на гірці має показовий розподіл із середнім значенням часу 20 хв. Знайти середню кількість потягів в черзі, середній час перебування складу в СМО, середній час перебування потяга в черзі.
27. Автозаправна станція (АЗС) має дві колонки. На майданчику біля неї одночасно може очікувати не більше чотирьох машин. Потік машин, що прибуває на станцію, найпростіший з інтенсивністю одна машина на хвилину. Час обслуговування автомашини розподілено за показовим законом із середнім значенням дві хвилини. Знайти для АЗС фінальні ймовірності стану для 1-, 2-, 3-х та 4-х машин, абсолютну пропускну здатність і ймовірність відмови в обслуговуванні.
28. Є двоканальна найпростіша СМО з відмовами. На її вхід надходить потік заявок з інтенсивністю чотири заявки в годину. Середній час обслуговування однієї заявки 0,8 год. Кожна обслугована заявка приносить дохід чотири гривні. Зміст кожного каналу обходиться 2 грн. за годину. Вирішити: вигідно чи не вигідно в економічних відносинах збільшити кількість каналів СМО до трьох, якщо дохід від заявок перебуває в співвідношенні D=Ac, де с – дохід від обслугованої заявки, А – абсолютна пропускна здатність СМО.
29. У стоматологічному кабінеті три крісла, а в коридорі є три стільці для очікування прийому. Потік клієнтів розподілений за найпростішим законом з інтенсивністю 12 клієнтів за годину. Час обслуговування клієнта розподілено показово із середнім значенням 20 хвилин. Якщо всі три стільці в коридорі зайняті, клієнти в чергу не стають. Визначити середню кількість клієнтів, що обслуговуються кабінетом за годину, середню частку обслугованих клієнтів із тих, що прийшли та середній час, що клієнт проведе в коридорі та в кабінеті.
30. Квиткову касу з одним віконцем подано як СМО з необмеженою чергою. Каса продає квитки в пункти А і В; пасажирів, що бажають купити квиток у пункт А, приходить в середньому троє за 20 хвилин, а в пункт В – двоє за 20 хвилин. Потік пасажирів можна вважати найпростішим. Касир у середньому обслуговує трьох пасажирів за 10 хвилин. Час обслуговування розподілений за показовим законом. Установити, чи існують фінальні ймовірності станів СМО, і якщо так – обчислити перші три з них. Знайти середню кількість заявок у СМО, середній час перебування заявки в системі й середню кількість заявок у черзі.
31. Залізнична каса має два віконця, у кожному з яких продаються квитки у два пункти: Москву й Петербург. Продаж квитків в обидва напрямки однаковий за інтенсивністю, що дорівнює 0,45 пасажирів за хвилину. Середній час обслуговування пасажира (продаж йому квитка) 2 хвилини. Надійшла раціоналізаторська пропозиція: для зменшення черг (в інтересах пасажирів) зробити обидві каси спеціалізованими. У першій продавати квитки тільки в Петербург, а в другій – тільки в Москву. Вважати всі потоки подій найпростішими. Потрібно перевірити розумність цієї пропозиції.
32. Розглядається найпростіша двоканальна СМО з «нетерплячими» заявками. Інтенсивність потоку заявок три заявки за годину; середній час обслуговування однієї заявки 1 година; середній термін, протягом якого заявка «терпляче» очікує в черзі, дорівнює 0,5 год. Підрахувати фінальні ймовірності станів, обмежуючись тими, які не менше 0,001. Знайти відносні й абсолютну пропускні здатності.
33. Ремонтний майстер обслуговує групу з восьми касових автоматів із продажу квитків у приміські поїзди. Спостереження показали, що в середньому автомат вимагає втручання майстра один раз за 2 год. Потік вимог на ремонт – найпростіший. Усунення несправностей в автоматі займає в середньому 6 хв., причому час ремонту є величина випадкова, розподілена за показовим законом. Визначити коефіцієнт простою майстра й середню довжину черги автоматів на обслуговування.
34. АТС має шість ліній зв'язку. Потік вимог на переговори – найпростіший з інтенсивністю один виклик за хвилину. Середній час переговорів – 3 хв. Закон розподілу часу показовий. Визначити ймовірність відмови й коефіцієнт завантаження ліній зв'язку.
35. На станції метро п’ять касових апаратів. Зі спостережень установили, що до цих п'яти апаратів підходять в середньому 60 осіб за хвилину. Час обслуговування вважатимемо розподіленим за показовим законом, із середнім часом обслуговування 4 сек. Знайти ймовірність того, що всі апарати вільні, та середню кількість осіб, що перебувають біля апаратів.
36. У камеру схову вокзалу, що складається з п’яти секцій, надходить найпростіший потік вимог у середньому дві вимоги у хвилину. Час обслуговування розподілений за показовим законом і складає в середньому дві хвилини. Час очікування в черзі – в середньому чотири хвилини й розподілено за показовим законом. Визначити середню довжину черги, середню кількість зайнятих секцій і відносну пропускну здатність системи.
37. У залізничній поліклініці в кабінеті флюорографії проходить прийом в середньому дві особи за хвилину. Час прийому розподілений за показовим законом. Потік відвідувачів найпростіший з інтенсивністю п’ять осіб за хвилину. Черга відвідувачів, які очікують прийом, не обмежена. Визначити середню довжину черги й абсолютну пропускну здатність кабінету флюорографії.
38. Залізнична сортувальна гірка, на яку подається найпростіший потік потягів з інтенсивністю два потяги за годину, є СМО з необмеженою чергою. Час обслуговування (розпуску) потяга на гірці має показовий розподіл із середнім значенням часу 15 хв. Знайти середню кількість потягів у черзі, середній час перебування потяга в черзі, а також абсолютну пропускну здатність сортувальної гірки.
39. На базу даних (БД) сервера залізниці надходить 10 запитів за секунду. Середній час обробки кожного запиту – одна секунда. Запит, що надійшов у момент обробки попереднього запиту, стає в чергу. Визначити ймовірність наявності черги, ймовірність відсутності запиту й коефіцієнт завантаження сервера.
3.9 Завдання до самостійної роботи №3
Побудувати графік розподілу Pk для N-канальної СМО з відмовами, якщо на вхід системи надходить найпростіший потік вимог з інтенсивністю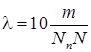 
та обслуговування вимог виконується з інтенсивністю 
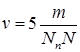, де m–остання цифра року (якщо вона дорівнює 0, то підставляємо 10), N – кількість каналів обслуговування, Nn – номер за списком. Кількість каналів обслуговування визначається за таблицею 1.
Приклад. Для СМО з відмовами графік розподілу Pk, побудований в системі Mathlab, зображений на рис. З.1.
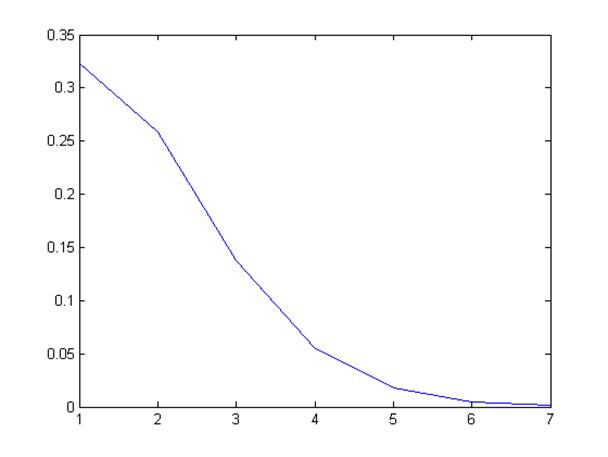
Рисунок 3.1 – Графік ймовірностей Pk
Визначити характеристики якості обслуговування для СМО з відмовами:
1. Ймовірність відмови Рвідм.
2. Середню кількість зайнятих вузлів Мзайн.
3. Середню кількість вільних вузлів Мвіл.
4. Відносну пропускну здатність Q.
5. Абсолютну пропускну здатність А.
6. Коефіцієнт зайнятості вузлів Кз.
3.10 Завдання до самостійної роботи №4
Побудувати графік ймовірності станів Pk, для N-канальної СМО з очікуванням, якщо на вхід надходить найпростіший потік вимог з інтенсивністю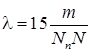 
та обслуговування вимог виконується з інтенсивністю 
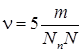, де Nп – номер за списком, m – остання цифра року (якщо вона дорівнює 0, то підставляємо 10), N – кількість каналів обслуговування. Кількість каналів обслуговування визначається за таблицею 3.1.
Таблиця 3.1
| Nп, | 1,5,9,13,17,21 | 2,6,10,14,18,22 | 3,7,11,15,19,23 | 4,8,12,16,20,24 |
| N |
Приклад. Для СМО з очікуванням графік розподілу Pk, побудований в системі Mathlab, зображений на рис. 3.2.
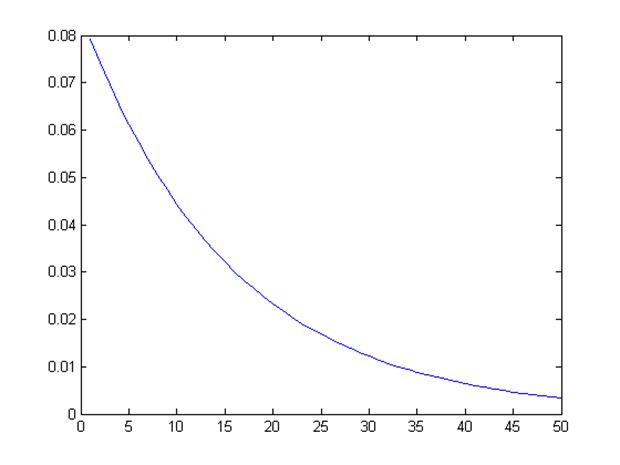
Рисунок 3.2 – Графік ймовірностей Pk
Визначити характеристики якості обслуговування:
1. Ймовірність наявності черги Pk.
2. Ймовірність зайнятості всіх вузлів системи Pзайн.
3. Середню кількість вимог у системі Мвим.
4. Середню довжину черги Mчер.
5. Середню кількість вільних вузлів Мвіл.
6. Середню кількість зайнятих вузлів Мзайн.
7. Середній час очікування Точ.
8. Загальний час перебування вимог у черзі за одиницю часу Тз.оч.
9. Середній час перебування вимоги в системі Твим.
10. Сумарний час, що проводять всі вимоги за одиницю часу Тс.вим.
11. Абсолютну пропускну здатність А.