Методика дискриминантного анализа

Дискриминантный анализ – это совокупность методов, позволяющих решать задачи идентификации объектов по заданному набору характерных признаков.

Весь процесс проведения дискриминантного анализа разбивается на два этапа и каждый из них можно рассматривать как совершенно самостоятельный метод.

Первый этап – выявление и формальное описание различий между существующими множествами (группами) наблюдаемых объектов.

Второй этап – непосредственная классификация новых объектов, т.е. отнесение каждого объекта к одному из существующих множеств.

Пусть имеется множество единиц наблюдения, каждая из которых характеризуется несколькими признаками (переменными): 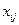– значения j-й переменной у i-гообъекта ; .

Предположим, что все множество объектов разбито на несколько подмножеств (два и более). Из каждого подмножества взята выборка объемом , где – номер подмножества (класса) .

Признаки, которые используются для того, чтобы отличать одно подмножество от другого, называются дискриминантными переменными.

Число дискриминантных переменных не ограничено, но на практике выбор должен осуществляться на основании логического анализа исходной информации. Число объектов наблюдения должно превышать число дискриминантных переменных, т.е. . Предполагается, что дискриминантные переменные – линейно независимые нормально распределенные многомерные величины.

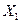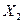Рассмотрим случай для двух дискриминантных переменных. Функция называется канонической дискриминантной функцией, а величины и – дискриминантными переменными

. (1.1)

Дискриминантная функция может быть как линейной, так и нелинейной. Выбор вида этой функции зависит от геометрического расположения разделяемых классов в пространстве дискриминантных переменных.

Коэффициенты дискриминантной функции ( ) определяются таким образом, чтобы и как можно больше отличались между собой.

Вектор коэффициентов дискриминантной функции ( 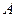) определяется по формуле

. (1.2)

Полученные значения коэффициентов подставляют в формулу (1.1) и для каждого объекта в обоих множествах вычисляют дискриминантные функции , затем находят среднее значение для каждой группы ( ). Таким образом, каждому -му наблюдению, которое первоначально описывалось -переменными, будет соответствовать одно значение дискриминантной функции, и размерность признакового пространства снижается.

Классификация при наличии двух обучающих выборок.Перед тем как приступить непосредственно к процедуре классификации, нужно определить границу, разделяющую два множества. Такой величиной может быть значение функции, равноудаленное от и , т.е.

. (1.3)

Величина с называется константой дискриминации.

Объекты, расположенные над разделяющей поверхностью находятся ближе к центру множества ,следовательно, могут быть отнесены к первой группе, а объекты, расположенные ниже этой поверхности, ближе к центру второго множества, т.е. относятся ко второй группе. Если граница между группами будет выбрана как сказано выше, то вэтом случае суммарная вероятность ошибочной классификации будет минимальной.

Классификация при наличии -обучающих выборок.Рассмотрим особенности классификации объектов, возникающие при наличии -обучающих выборок (>2). Как и в случае с двумя обучающими выборками, предполагается, что каждое множество является нормально распределенным с различными векторами средних значений. Оценка совместной ковариационной матрицы рассчитывается по следующей формуле:

, (1.4)

где – количество обучающих выборок; – матрица ковариации для i-й выборки; – численность i-й выборки.

В этом случае каждому множеству ставится в соответствие своя дискриминантная функция вида

.

Вектор коэффициентов этой функции ( ) рассчитывается по формуле , а свободный член .

Новый классифицируемый объект с переменными будет отнесен к тому множеству , для которого величина будет максимальной.

В заключение необходимо отметить, что в данном параграфе рассмотрен только один из методов проведения дискриминантного анализа. Более подробно другие методы и алгоритмы дискриминантного анализа описаны в специальной литературе.

1.2. Примеры решения типовых задач

Пример 1. Имеются следующие данные по двум группам промышленных предприятий (таблица 1.1).

Таблица 1.1

Первая группа ()	Вторая группа ()
Номер предприятия	Удельный вес потерь от брака, % ( 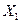)	Фондоотдача активной части основных фондов, ден. ед. ( 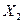)	Номер предприятия	Удельный вес потерь от брака, % ( )	Фондоотдача активной части основных фондов, ден. ед. ( )
	0,15	1,91		0,48	0,88
	0,34	1,68		0,41	0,62
	0,09	1,89		0,62	1,09
	0,21	2,30		0,50	1,32
				1,20	0,68
–	=0,198	= 1,945	—	= 0,642	=0,918

1. На основании приведенных данных следует найти оценки векторов средних , и ковариационных матриц ( , )а также оценку суммарной ковариационной матрицы ( ) и обратной к ней ( ).

2. Рассчитайте вектор оценок коэффициентов дискриминантной функции (А)и определите ее средние значения для каждого множества. Определите константу дискриминации ( ).

Вычислите оценки значений дискриминантной функции для предприятия, у которого переменные принимают значения: удельный вес потерь от брака ( )равен 0,2%; фондоотдача активной части основных фондов ( )равна 0,75 ден. ед.

Определите, к какой из двух групп следует отнести данное предприятие.

Решение. 1. Для каждой группы предприятий рассчитаем ковариационные матрицы.

Первая группа ():

,

.

Вторая группа ( ):

,

.

Совместная ковариационная матрица и обратная матрица будут иметь следующий вид:

;

.

2. Вектор коэффициентов дискриминантной функции (А)равен

.

Вектор значений дискриминантной функции для первого подмножества

.

Вектор значений дискриминантной функции для второго подмножества

.

Средние значения дискриминантной функции и константа дискриминации

.

3. Рассчитаем значение дискриминантной функции для предприятия со значениями переменных равными ;

.

Так как полученное значение дискриминантной функции для рассматриваемого предприятия =8,844<с=16,770, его следует отнести ко второму подмножеству.

Пример 2. Рассмотрим пример проведения дискриминантного анализа при наличии трех обучающих выборок.

Для того чтобы проще было изобразить на рисунке объекты каждого из подмножества, предположим, что каждый объект (предприятие) характеризуется только двумя переменными:

Первое подмножество

Номер объекта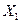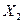
	9,4	1,9
	9,9	1,7
	9,1	2,3
	10,0	2,6
	9,4	2,0
	9,0	1,9
	=9,47	=2,07

Второе подмножество

Номер объекта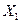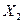
	7,4	1,09
	6,7	1,23
	6,6	1,33
	7,0	1,25
	7,5	1,15
	=7,04	=1,21

Третье подмножество

Номер объекта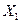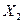
	5,5	0,9
	5,1	0,88
	5,4	1,20
	5,8	1,25
	=5,45	=1,06

Здесь: 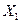– выработка продукции на одного работающего, тыс. ден. ед.: 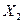– фондоотдача основных производственных фондов, ден. ед.

Для каждого подмножества объектов определяем ковариационную матрицу:

- для первого подмножества

;

- для второго подмножества

;

- для третьего подмножества

.

Для каждой из существующих пар подмножеств рассчитаем совместные ковариационные матрицы и матрицы, обратные к ним.

Совместная ковариационная матрица и обратная к ней матрица для первого и второго подмножеств

.

Определяем разность векторов средних величин .

Совместная ковариационная матрица и обратная к ней матрица для первого и третьего подмножеств

.

Разность векторов средних значений .

Наконец, совместная ковариационная матрица и обратная к ней матрица для второго и третьего подмножеств

;

.

Разность векторов средних значений .

На основании обратных матриц , , и разностей векторов средних значений определим для каждой пары подмножеств векторы коэффициентов дискриминантных функций:

;

;

.

Определяем значения дискриминантных функций по матрице значений исходных переменных в каждом подмножестве.

Для разграничения первого и второго подмножеств имеем

;

- среднее значение дискриминантной функции для первого подмножества .

- среднее значение дискриминантной функции для второго подмножества .

Для первого и второго подмножеств константа дискриминации равна:

Для разграничения первого и третьего подмножеств имеем

;

- среднее значение дискриминантной функции для первого подмножества ;

;

- среднее значение дискриминантной функции для третьего подмножества .

Для разграничения первого и третьего подмножеств константа дискриминации равна:

.

Для разграничения второго и третьего подмножеств имеем

;

- среднее значение дискриминантной функции для второго подмножества .

;

- среднее значение дискриминантной функции для третьего подмножества .

Для разграничения второго и третьего подмножеств константа дискриминации равна:

.

В общем виде дискриминантные функции для трех подмножеств имеют вид:

Следовательно, границы трех классов будут определяться системой уравнений

(1.5)

Чтобы начать классификацию новых объектов, подставим значения исходных переменных в выражение (1.5) и сравним полученные результаты с нулем,

если и , то объект принадлежит первому множеству;

и , то объект принадлежит второму множеству;

и , то объект принадлежит третьему множеству.

Пример 3. По результатам анализа финансовой устойчивости предприятий экспертным путем были выделены три группы предприятий, характеризующиеся двумя переменными: 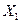– рентабельность основной деятельности предприятия; – коэффициент абсолютной ликвидности (таблица 1.2).

Таблица 1.2

I группа	II группа	III группа
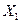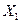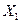8,7
	7,5
	9,8

Примечание.

;

.

Решение.

1. Для каждой из групп рассчитаем вектор средних значений и матрицу ковариаций:

- для I группы ;

;

- для II группы ;

;

- для III группы ;

.

2. Рассчитаем три дискриминантные функции:

I группа

Вектор коэффициентов дискриминантной функции:

;

свободный член

.

Дискриминантная функция будет иметь следующий вид:

.

II группа

Вектор коэффициентов дискриминантной функции:

;

свободный член

.

Дискриминантная функция будет иметь следующий вид:

.

III группа

Вектор коэффициентов дискриминантной функции:

;

свободный член

.

Дискриминантная функция будет иметь следующий вид:

.

Итак, получены три дискриминантные функции:

;

;

.

Теперь можно начинать процедуру классификации новых объектов. Предположим, что рассматривается предприятие, которое имеет следующие значения дискриминантных переменных: , .

Подставляем поочередно эти значения в каждую из дискриминантных функций:

;

;

.

Так как и , новый объект следует отнести ко второй группе предприятий.

Техническое задание на разработку программного средства

Введение

Настоящее техническое задание распространяется на разработку информационно-аналитической системы на основе методов теории статистических решений в различных предметных областях.

Широкий круг задач разработки приложений систем поддержки принятия решений относятся к классу теории статистических решений, методы решения которых, как правило, имеют экспоненциальную вычислительную сложность.

В то же время эти методы и алгоритмы не систематизированы, оценки их вычислительной и емкостной сложности и сведения о возможной точности получаемых решений неполны и разбросаны по многим источникам. В рамках единой системы не существует программной реализации даже для ограниченного круга алгоритмов решения основных задач теории статистических решений

Создание системы, в рамках которой были бы реализованы наиболее часто упоминаемые методы и алгоритмы решения задач теории статистических решений, позволит как оценивать и исследовать отдельные методы и алгоритмы, так и сравнивать их с точки зрения затрат вычислительных ресурсов и точности получаемых решений

Основание для разработки

Приложение для информационно-аналитической системы разрабатывается на основании учебного плана подготовки бакалавров по по дисциплине «Системы автоматизации разработки программного обеспечения».

Назначение

Первая версия системы предназначена для решения небольшого круга задач теории статистических решений (проверка статистических гипотез, корреляционны анализ, кластерный анализ). В следующих версиях предполагается увеличение количества решаемых задач.

Пользователями могут выступать научные работники и инженеры, занимающиеся разработкой систем поддержки принятия решений. Пользователями могут также быть и специалисты других предметных областей, которым приходится решать подобные задачи.