Метод псевдослучайного интервала

В рассмотренном выше простейшем случае выполняется замена НЗБ всех последовательно размещенных пикселей изображения. Другой подход — метод случайного интервала [78], заключается в случайно распределении битов секретного сообщения по контейнеру, в результате чего расстояние между двумя встроенными битами определяется псевдослучайно. Эта методика особенно эффективна в случае, когда битовая длина секретного сообщения существенно меньше количества пикселей изображения.

Рассмотрим простейший случай этого метода, когда интервал между двумя последовательными встраиваниями битов сообщения является функцией координат предыдущего модифицированного пикселя.

Шаг1

Пусть сообщение, которое необходимо скрыть; M:=" © Пузыренко А.Ю., 2005 г.". В качестве контейнера С используем подмассив В синего цветового компонента .изображения рис. 5.3.

Шаг2

Определим метки, которые будут устанавливать границы полезного сообщения в контейнере. В отличие от предыдущего метода, стартовая метка будет определять порядковый номер элемента контейнера, начиная с которого в последний будут заноситься данные. Пусть 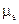:=154. Метка 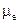будет сигнализировать о завершении полезной части среди извлеченных символов: 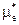:= "KiHeu,6"

Шаг 3

Примем, что при внесении битой сообщения в контейнер со сменным шагом, величина последнего обусловлена количеством единиц в двоичном значении номера элемента контейнера, который модифицировался предварительно. Доя подсчета величины шага (интервала) воспользуемся модулем (М.15), суммирующим количество элементов матрицы-столбца х, значение которых равно 1.

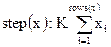(M.15)

Коэффициент К в данном случае стартовая метка должна иметь значение, близкое к наибольшему значению индекса элементов контейнера). Также при выборе К следует принимать во внимание общее количество бит, необходимых для скрытия сообщения, а также имеющееся количество элементов массива контейнера. Пусть К := 9.

Ограничивающую метку 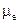, с помощью строчной функции concat(), объединяющей строки, выступающие в качестве ее аргументов, прибавим к тексту сообщения, которое подлежит скрытию. Результат объединения преобразуем в вектор ASCII-кодов: 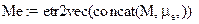Общее количество символов в полученном сообщении: rows(Me)=32 . Количество НЗБ контейнера, которое для этого необходимо (8 бит/символ):

8 rows(Me)=256 бит.

Шаг 4

Развернем массив В в вектор (М.16), на основе которого сформируем новый , вектор, содержащий скрытое сообщение (М.17). ',

Каждый символ сообщения Me (операция цикла for. 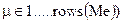.rows(Me)) перево-; дится в двоичный формат, (переменная b), каждый разряд которого записывается ] вместо самого младшего бита числа Р, соответствующего значению интенсивности синего цвета определенного пикселя. При этом элементы массива Cv перебираются не последовательно, а с переменным шагом, величина которого обусловлена функцией step( 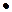)[7].

Стартовый элемент задается меткой 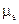. После проведенного изменения, модифицированное двоичное число Р переводится в формат десятичного и записывается в соответствующую позицию вектора Sv, который в начале модуля был принят равным вектору Cv.

Шаг 5

Обратное свертывание вектора Sv в массив, имеющий размерность контейнера, выполняется, с использованием модуля (М.7) с тем лишь отличием, что аргументом функций размерности массива (rows и cols) является массив В. Чтобы оценить степень "рассеяния" бит скрытого сообщения по массиву контейнера, в качестве примера рассмотрим результат присвоения пикселю, в который планировалось ввести бит сообщения, нулевого значения интенсивности (черный цвет) при предварительном общем осветлении изображения (рис. 5.9).

Рис. 5.9 Рассеяние битов сообщения по массиву контейнера '

Шаг 6

Результирующее цветное изображение будет определяться массивом объединения цветовых массивов: S := augment(R, G, S').

Шаг 7

При извлечении скрытого сообщения должны быть известны параметры 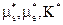и, разумеется, массив В*, который, как предполагается, содержит скрытые данные.

Развертывание массива В* в вектор Sv* выполняется с помощью аналогичного (М.16) модуля. Извлечение сообщения из вектора Sv* выполняется с помощью модуля (М.18) в обратном, по отношению к операции встраивания порядке.

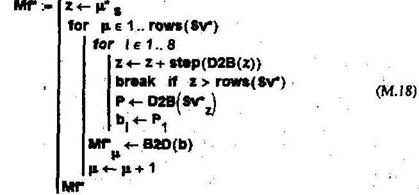
Из подученного вектора МГ путем сравнения с меткой ц", выделенного фрагмента извлекается полезное сообщение М* (МЛ 9).

М* = "© Пузыренко А.Ю., 2005 г.".

Результаты вычисления визуального искажения объединены в табл. 5.1 (стр. 125)