Метод псевдослучайной перестановки

Недостатком метода псевдослучайного интервала является то, что биты сообщения в контейнере размещены в той же последовательности, что и в самом сообщении, и только интервал между ними изменяется псевдослучайно. Поэтому для контейнеров фиксированного размера более целесообразным является использование метода псевдослучайной перестановки (выбора) [79], смысл которого заключается в том, что генератор ПСЧ образует последовательность индексов 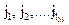и сохраняет k-й бит сообщения в пикселе с индексом .

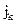Пусть N — общее количество бит (самых младших) в имеющемся контейнере; P^N — перестановка чисел {1,2,.... N). Тогда, если у нас имеется для скрытия конфиденциальное сообщение длиной n бит, то эти биты можно просто встроить вместо бит контейнера .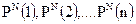

функция перестановки должна быть псевдослучайной, иными словами, она должна обеспечивать выбор бит контейнера приблизительно случайным образом. Таким образом, секретные биты будут равномерно распределены по всему битовому пространству контейнера. Однако при этом индекс определенного бита контейнера может появиться в последовательности более одного раза и в этом случае может произойти "пересечение" — искажение уже встроенного бита. Если количество бит сообщения намного меньше количества младших бит изображения, то вероятность пересечения является незначительной, и искаженные биты в дальнейшем могут быть восстановлены с помощью корректирующих кодов.

Вероятность, по крайней мере, одного пересечения оценивается как

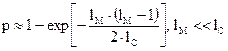(5.1)

При увеличени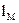и и 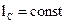данная вероятность стремится к единице.

Для предотвращения пересечений можно запоминать все индексы использованных элементов j_i и перед модификацией нового пикселя выполнять предварительную его проверку на повторяемость. Также можно применять генераторы ПСЧ без повторяемости чисел. Последний случай рассмотрим более подробно.

Для наших целей функция перестановки также зависит от секретного ключа К. При этом генератор псевдослучайной перестановки P^N -— это функция, которая для каждого значения К вырабатывает различные псевдослучайные перестановки чисел {1,2, ...,N}.

Обозначим через 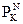генератор перестановок с соответствующим ключом К. Если перестановка 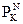защищена по вычислению (то есть, взлом алгоритма требует неоправданно больших затрат вычислительных ресурсов нарушителя), то возможность раскрытия содержания или предположение самого только вида перестановок без владения информацией о секретном ключе К практически равняется нулю.

Секретный генератор псевдослучайной перестановки (ГПСП) может быть эффективно реализован на основе генератора псевдослучайной функции (ГПСФ) [98], который, как и ГПСП, вырабатывает различные, не подлежащие прогнозированию функции при каждом отдельном значении ключа; однако множество значений функций не должно равняться области ее определения. ГПСФ легко реализуется из секретной хэш-функции Н путем объединения аргумента i с секретным ключом К и взятия от результирующей битовой строки функции Н:

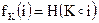(5.2)

где 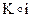— объединение (конкатенация) битовых строк К и i; 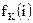— результирующая псевдослучайная функция от i, которая зависит от параметра К.

Генератор Луби (Luby) и Рекоффа (Reckoff) построен следующим образом. Запись вида 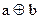подразумевает побитовое сложение по модулю 2 аргумента а с аргументом b, причем результат сложения имеет ту же размерность, что и а.

Пусть i— строка двоичных данных длиной 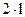.Разделим i на две части: х и у длиной l каждая, а ключ К— на четыре части: К₁,К₂,К₃,К₄. Тогда

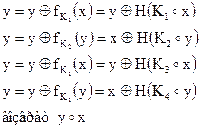
Для каждого значения ключа К алгоритм возвращает псевдослучайную перестановку из чисел 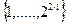Луби и Рекофф показали, что предлагаемая перестановка является настолько же секретной, насколько и генератор ПСФ. Они также предложили простой алгоритм перестановки из 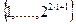. Если значение функции 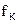представляет собой достаточно длинные битовые последовательности, тот же эффект можно получить, приняв, что у — первые l бит строки i, а х — последние 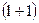бит.

Представленная выше конструкция позволяет получить перестановку 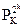из 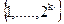для произвольного k. Однако в случае, когда количество бит контейнер составляет N, возникает необходимость перестановки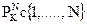

Преимущество метода, предложенного в [79], заключается в том, что существует возможность ограничиться только имеющимися для 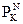аргументами. Пусть 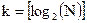(квадратные скобки означают округление к наименьшему целому, которое больше или равно аргументу). Тогда 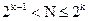. При этом подсчитываются значения 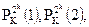... и из последовательности удаляются любые числа, превышающие N. Таким образом, получают значения 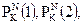… Заметим, что это становится возможным, когда функция перестановки вычислена для возрастающих значений аргументов, начиная с единицы. Следовательно, генератор ПСП 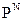для произвольного N может быть построен на основе, алгоритма Луби и Рекоффа.

Если же N является составным (как в случае изображения), существует более удобный способ построения ГПСП. Представленные ниже алгоритм основан на блочном кодировании с произвольным размером блока [79, 99]. Количество бит контейнера должно представлять собой составное число из двух сомножителей приблизительно одинакового порядка то есть 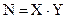для некоторых Х и Y.

В случае, когда данные скрываются в НЗБ пикселей цифрового изображения, параметры X и Y являются размерами данного изображения. Для получения координаті-го пикселя изображения при скрытии бита сообщения 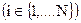необходимо выполнить следующие вычисления:

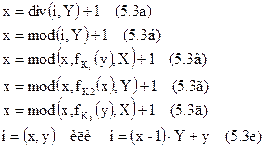
где div(i,X) и mod(i,X) — функции, которые возвращают, соответственно, целое и остаток от деления i на X. Другой вариант формулы (5.3 е) применим в случае, если массив изображения предварительно был развернут в вектор (по строкам). Прибавление единицы необходимо при индексации элементов массива изображения, начиная с единицы.

Первые два раунда алгоритма ((5.3а) - (5.3г)) необходимы для того, чтобы "рассеять" биты скрываемого сообщения среди наименее значимых бит контейнера. При этом первый раунд придает случайный характер x-координатам пикселя-контейнера, а второй — у-координатам. Третий раунд необходим для противодействия атаке на открытый (незашифрованный) текст.

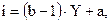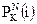В случае использования только двух раундов, пусть а — значение перестановки. Если криптоаналитик способен предположить значение а и может получить пару "открытый текст — кодированный текст" 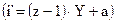для некоторого z, то он способен установить b. Несмотря на то, что авторы [79] считают, что предложенный ими алгоритм будет достаточно устойчивым и с тремя раундами, они признают, что в некоторых случаях может понадобиться четы а ре или более раундов, что должно повысить устойчивость алгоритма к взлому.

Промоделируем данный метод в программе MathCAD.

Шаг 1

Сообщение, которое необходимо скрыть: М="© Пузыренко А.Ю., 2005 г.".

Контейнер С— подмассив Всиней цветовой составляющей изображения рис. 5.3. При этом количество бит в сообщении: L_M :strlen(M), L_M=200 бит; геометрические размеры контейнера: X:=rows(C), X=128 пикселей; Y :=cols(C), Y=128 пикселей; N = X Y,

N = 16384.

Шаг 2

Для формирования ключа используем модуль (М.20), который позволяет на основании первичного ключа 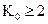сформировать вектор, который будет содержать 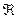пар ключей (каждая пара ключей будет использоваться в соответствующем раунде вычисления координат x и у).

В данном модуле поочередно используются три функции:

• num2str(d) — преобразование аргумента-числа в соответствующую строку А;

• substr(A,0, 3) — выделение фрагмента строки А, который содержит три первых символа строки;

• str2num(a)— обратное преобразование а-фрагмента в число, которое и присваивается s-му элементу массива К.

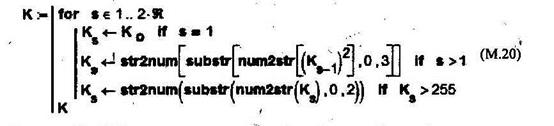
В случае К_s>255 с помощью аналогичной комбинации функций число сокращaется на один символ.

Рассмотрим пример вычисления пар ключей при К_о=125 и 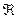=6 (рис. S.10).

KT=

Рис. 6.10. Пример вычисления ключей К

Шаг 3

Встраивание бит сообщения в псевдослучайные пиксели контейнера выполним с помощью модуля (М.21), который реализует алгоритм (5.3). В начале модуля массиву Sприсваиваются значения исходного массива С. Также выполняется конвертирование сообщения из строкового формата в вектор двоичных данных M_{vec_bin}. При вычислении координат хи у используется операция векторизации, которая позволяет поэлементно складывать по модулю 2 двоичные векторы К и у (или х). При этом размерность указанных векторов должна быть одинаковой, для чего используется функция submatrix .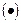

Оценим степень "рассеяния" бит сообщения по массиву контейнера при разном количестве раундов 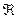вычисления координат х и у (рис. 5.11, формирование которого проводится аналогично формированию рис. 5.9).

Рис. 5.11. Рассеяние бит сообщения по массиву контейнера при изменении параметра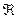

Как видим, приемлемый уровень рассеяния достигается уже при 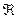=4.

Шаг 4

На принимающей стороне должны быть известны первичный ключ 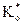и массив цветности, в который выполнялось встраивание (S*). Из последнего получаются значения X*, Y*, N*. Модуль, предназначенный для извлечения скрытого сообщения, представлен ниже (М.22).

Отметим, что в данном и последующих методах предварительное добавление стартовой и конечной меток к встраиваемому сообщению не выполняется. Соответственно, при извлечении строка символов, кроме полезного содержания, будет содержать еще и произвольный набор символов, входящих в кодировку ASCH.

Отсутствие в последующих модулях этапов выделения полезного сообщения из всего множества символов никоим образом не говорит о невозможности осуществления данной операции. При желании, представленные модули можно легко адаптировать для осуществления поиска предварительно встроенных меток (по аналогии с рассмотренными выше методами).

Результаты вычисления визуального искажения сведены в табл. 5.1 (стр. 125).

Метод блочного скрытия

Метод блочного скрытия — это еще один подход к реализации метода замены и заключается в следующем [3]. Изображение-оригинал разбивается на 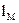непересекающихся блоков 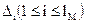произвольной конфигурации, для каждого из которых вычисляется бит четности :

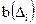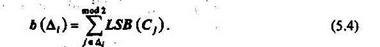
В каждом блоке выполняется скрытие одного секретного бита M_i, Если бит четности, 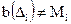то происходит инвертирование одного из НЗБ блока 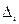, в результате чего 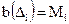. Выбор блока может происходить псевдослучайно с использованием стегакоключа.

Хотя этот метод имеет такую же низкую устойчивость к искажениям, как и все предыдущие, у него есть ряд преимуществ. Во-первых, существует возможность модифицировать значение такого пикселя в блоке, изменение которого приведет к минимальному изменению статистики контейнера. Во-вторых, влияние последствий встраивания секретных данных в контейнер можно уменьшить за счет увеличения размера блока.

Рассмотрим пример программы в MathCAD, которая позволяет выполнить стеганографическую защиту текстового сообщения методом блочного скрытия.

Шаг 1

Исходные данные соответствуют; принятым при моделировании предыдущего метода.

Шаг 2

Разбиение массива контейнера на блоки выполним следующим образом: если количество бит в сообщении 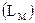не превышает количества столбцов Yмассива С, то один блок соответствует отдельному столбцу массива С. Если же 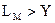, то один блок равен 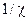от отдельного столбца массива, где 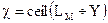Значение 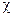должно быть известно получателю.

Данный алгоритм встраивания реализован в модуле (М.23). Начало модуля аналогично модулю (М.21). Счетчик 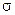позволяет выделять соответствующую соотношению 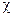часть от общей размерности столбца массива. При этом определяются индексы строк, начиная с которой (r1)и по которую (r2)выделяется фрагмент 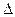у-го столбца.

Для каждого блока 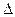выполняется вычисление бита четности b, Если b не равен текущему значению бита сообщения, то из блока 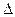случайным образом выбирается индекс n пикселя, интенсивность цвета которого увеличивается или уменьшается на единицу, в зависимости от того, четным или нечетным является его первичное значение. С помощью функции 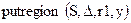выполняется встраивание модифицированного массива 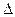в общий массив S, начиная со строки r1 и столбца у в сторону самых старших индексов строк и столбцов соответственно.

Рис. 5.12. Рассеяние бит сообщения по массиву контейнера

На рис. 5.12 изображены пиксели контейнера, интенсивность цвета которых претерпела изменения (для наглядности, цвет данных пикселей установлен черным).

Очевиден факт снижения количества модифицированных пикселей по сравнению с результатом применения двух предыдущих методов (см. рис. 5.9 и рис. 5.11).

Шаг 3

Извлечение секретной информации осуществляется с помощью модуля (М.24). Результаты вычисления визуального искажения сведены в табл. 5.1(стр. 125)

Методы замены палитры

Для скрытия данных можно также воспользоваться палитрой цветов, присутствующих в формате изображения [80]. Палитра из N цветов определяется как список пар индексов 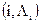, который определяет соответствие между индексом i и его вектором цветности 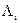(так называемая таблица цветов). Каждому пикселю изображения ставится в соответствие определенный индекс в таблице. Поскольку порядок цветов в палитре не важен для восстановления общего изображения, конфиденциальная информация может быть скрыта путем перестановки цветов в палитре.

Существует N! различных способов перестановки N-цветной палитры, чего вполне достаточно для скрытия небольшого сообщении. Однако методы скрытия, в основе которых лежит порядок формирования палитры, также являются неустойчивыми: любая атака, связанная со сменой палитры, уничтожает встроенное сообщение.

Чаще всего соседние цвета в палитре не обязательно похожи, поэтому некоторые стеганометоды перед скрытием данных упорядочивают палитру таким образом, что смежные цвета становятся подобными. Например, значение цвета может быть упорядочено по расстоянию d в RGB-пространстве, где 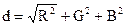[3].

Поскольку ЗСЧ более чувствительна к изменениям яркости цвета, то целесообразно сортировать содержание палитры именно по значениям яркости сигнала. После сортировки палитры можно изменять НЗБ индексов цвета без чрезмерного искажения изображения.

Некоторые стеганометоды [81] предусматривают уменьшение общего количества значений цветов (до N/2) путем "размывания" изображения. При этом элементы палитры дублируются таким образом, чтобы значение цветов для них различалось несущественно. В итоге каждое значение цвета размытого изображения соответствует двум элементам палитры, которые выбираются в соответствии с битом скрываемого сообщения.

Можно предложить следующий вариант метода замени палитры.

Шаг 1

Исходные данные — стандартные.

Шаг 2

Таблицу цветов получаем, например, используя подмассив интенсивности красного R (M.25). Секретность таблицы будет определять алгоритм ее формирования на основе массива R.

Полученную таблицу Т упорядочим по интенсивности цветов с помощью функции csort(T,с), которая позволяет переставить строки массива Т таким образом, чтобы отсортированным оказался столбец с:

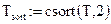
На рис. 5.13 представлены фрагменты оригинальной и отсортированной цветовых таблиц.

T=				Tsort=

Рис. 8.13. Оригинальная (Т) и отсортированная (Т_sort) цветовые таблицы

На рис. 5.14. представлена графическая интерпретация цветовых таблиц.

Рис. 6.14. Графическое отображение цветовых таблиц Т и Т_sort

Шаг 3

Модуль встраивания сообщения в контейнер (М.26) реализует следующий алгоритм.

Формирование битового вектора из символьной строки аналогично представленному в (М.21). Из массива контейнера С, путем перебора индексов строк (х) и столбцов (у), переменной pixприсваивается значение интенсивностей цвета соответствующих пикселей контейнера. Внутренним циклом 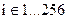выполняется поиск соответствующего значения интенсивности в отсортированной цветовой таблице Т_sort.

В случае положительного исхода поиска, переменной n присваивается значение индекса, соответствующего данной интенсивности в таблице Т(первый столбец Т_sort, а переменной 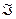— значение индекса, соответствующего данной интенсивности в таблице Тsort. Если НЗБ индекса n не равно текущему биту скрываемого сообщения, то происходит поиск ближайшего индекса, НЗБ которого равно биту сообщения. Поиск выполняется вниз (L) и вверх (Н) от индекса .

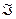Предварительное присвоение переменным 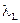и 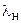значения -/+1000 гарантирует невозможность дублирования предыдущих значений 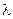, если продвижение вниз или вверх от индекса 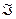не привело к выполнению поставленного условия (последнее возможно при обнаружении индекса 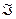слишком близко к нижней или верхней границе отсортированной цветовой таблицы).

Шаг 4

При извлечении сообщения, на основе массива R* необходимо сформировать таблицы цветов Т и Т_sort . Модуль, реализующий данную операцию, идентичен (М.25).

Шаг 5

Модуль извлечения (М.27) для интенсивности каждого пикселя массива S* выполняет поиск соответствующей интенсивности в цветовой таблице. При нахождении, 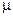-му элементу битового сообщения М* присваивается значение НЗБ индекса, соответствующее данной интенсивности в неотсортированной таблице. Полученный битовый вектор в конце модуля преобразуется в строку символов.

Результаты вычисления визуального искажения сведены в табл. 5.1 (стр. 125).