Ход работы. Серия 1 Количество бросаний, n = t /T Количество «нераспавшихся» монет, N Количество «распавшихся» монет N =N- N0
- Отсчитайте начальное количество монет N0= 128, перемешайте их в банке и высыпьте на разнос.
- Подсчитайте число «нераспавшихся» монет (т.е. число монет, лежащих «орлом» вверх), соберите их обратно в банку, снова перемешайте и высыпьте на разнос.
- Опыт повторите 10 раз.
- Заполните таблицы.
Серия 1
| Количество бросаний, n = t /T | Количество «нераспавшихся» монет, N | Количество «распавшихся» монет N 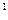 =N- N0 =N- N0 |
- Повторите серию бросаний монет еще дважды, начиная каждый раз с N(0)= 128.
Серия 2
| Количество бросаний, n = t /T | Количество «нераспавшихся» монет, N | Количество «распавшихся» монет N 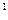 =N- N0 =N- N0 |
- Подобрав удобный масштаб, постройте график зависимости N=N(n) для двух серий разными цветами в одной системе координат. В этой же системе координат постройте график, соответствующий теоретической закономерности.
- Запишите вывод о том, что вы измеряли и какой получен результат.
