Коэффициент сопряженности признаков

Фи-коэффициент применяют только к таблице 2 х 2, а коэффициент сопряженности признаков С(contingency coefficient) используют для оценки тесноты связи в таблицах любого размера.

Коэффициент сопряженности признаков (contingency coefficient)

Мера тесноты связи в таблицах любого размера.

Коэффициент сопряженности признаков связан с Х² следующим образом:

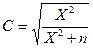
Значения коэффициента сопряженности находятся в диапазоне от 0 до 1. При отсутствии связи он равен нулю (т.е. переменные статистически независимы), но своего максимального значения (1) он никогда не достигает. Максимальное значение коэффициента сопряженности зависит от размера таблицы (числа рядков и колонок). Поэтому он используется только для сравнения таблиц одинакового размера. Значение коэффициента сопряженности для табл. 15.3 следующее:

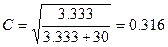
Это значение коэффициента сопряженности указывает на слабую связь. Другой статистикой, которую можно вычислить для любой таблицы, является V-коэффициент Крамера (Cramer).

V-коэффициент Крамера

V-коэффициент Крамера (Cramer's V) — это модифицированная версия коэффициента кор­реляции фи (ф), которую используют в таблицах, больших по размеру, чем 2x2.

V-коэффициент Крамера (Cramer's V)

Мера тесноты связи, используемая в таблицах, больших по размеру, чем 2x2.

Если для таблиц, больших, чем 2x2, вычисляют фи-коэффициент, то он не имеет верхней границы, V-коэффициент Крамера получают корректировкой фи-коэффициента или по числу рядов, или по числу колонок в таблице. Причем из двух значений выбирают меньшее. Коррек­тировку осуществляют так, что значения V-коэффициента лежат в диапазоне от 0 до 1. Большее значение V-коэффициента указывает на более сильную связь, но не указывает, как связаны пе­ременные. Для таблицы с rрядами и с колонками связь между V-коэффициентом Крамера и фи-коэффициентом выражается следующим образом:

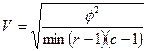или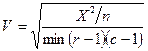

Значение V-коэффициент Крамера для табл. 15.3 равно:

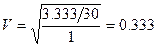
Таким образом, связь не очень сильна. В этом случае V = ф . Так всегда происходит для таб­лицы 2x2. Другой обычно рассчитываемой статистикой является коэффициент "лямбда".

Коэффициент "лямбда"

Коэффициент "лямбда" используется в том случае, когда переменные измерены с помо­щью номинальной шкалы. Асимметрический коэффициент "лямбда" (asymmetric lambda) по­казывает выраженное в процентах улучшение при прогнозировании значения зависимой пе­ременной при данном значении независимой переменной.

Асимметрический коэффициент "лямбда" (asymmetric lambda)

Мера выраженного в процентах улучшения прогнозирования значения зависимой перемен­ной при данном значении независимой переменной. Значения коэффициента "лямбда" ле­жат в пределах от 0 до 1.

Значения коэффициента "лямбда" лежат в пределах от 0 до 1. Значение "лямбда", равное 0, означает, что никакого улучшения в прогнозировании не наблюдается. Значение 1 указывает на то, что прогноз может быть сделан без ошибки. Это происходит тогда, когда каждая категория независимой переменной связана с одной категорией зависимой переменной.

Асимметрический коэффициент "лямбда" подсчитывают для каждой из зависимых переменных. Также рассчитывают симметричный коэффициент "лямбда" (symmetric lambda) - средним значением двух асимметричных значений.

Симметричный коэффициент "лямбда" (symmetric lambda)

Симметричный коэффициент "лямбда" не дает предположения о том, какая из переменных зависимая. Он измеряет общее улучшение прогнозирования, когда прогноз уже сделан в обоих направлениях.

Симметричный коэффициент "лямбда" не делает предположения о том, какая из переменных зависимая. Он измеряет общее улучшение, прогнозирования, когда прогноз уже выполнен в обоих направлениях [14]. Значение асимметричного коэффициента "лямбда" в табл. 15.3, если в качестве зависимой переменной взять использование Internet, равно 0,333. Это указывает на то, что знание пола увеличивает нашу возможность прогнозирования на0,333, т.е. имеет место улучшение прогнозирования на 0,33%. Симметричный коэффициент "лямбда" также равен 0,33%.

Другие статистики

Обратите внимание, что при вычислении значения х² переменные должны быть измерены по номинальной шкале. Для измерения связи между двумя порядковыми переменными применяют другие статистики, такие как may b, may с и гамма. Все эти статистики используют информацию об упорядочении категорий переменных, рассматривая каждую возможную пару случаев в таблице, чтобы определить, имеет ли первая переменная тот же относительный порядок расположения (ранг), что и вторая (конкордатное, согласованное расположение), или их расположения (ранги) имеют обратный порядок (несогласованное расположение), или их ранги совпадают (связанные ранги). Эти статистики отличаются только способом обработки рангов. Как тау b , так и тау b, корректируют по числу связанных рангов. Тау b(tau b) больше всего подходит для квадратных таблиц, в которых количество рядов и колонок равно.

Тау b (tau b)

Вычисляемая статистика, которая измеряет связь между двумя порядковыми переменными. Она вычисляется с учетом числа связанных рангов, и ее лучше использовать для квадратных таблиц.

Значения этой статистики лежат в пределах от +1 до — 1. Таким образом, можно определить направление (положительное или отрицательное) и силу (насколько близко данное значение находится к 1) связи. Для прямоугольной таблицы, в которой количество рядов отличается от количества колонок, следует использовать таус (tau с).

Тау с (tau с)

Вычисляемая статистика, измеряющая связь между двумя порядковыми переменными. Она вычисляется с учетом числа связанных рангов, и ее лучше использовать, когда таблица пе­ременных не квадратна, а прямоугольна.

Статистика "гамма" (gamma) не учитывает ни связанные ранги, ни размер таблицы. Зна­чения гаммы также лежат в пределах от +1 до — 1 и обычно имеет большее числовое значе­ние, чем тау b и тау с.

Статистика "гамма" (gamma)

Вычисляемая статистика, измеряющая связь между двумя порядковыми переменными. Она не делает поправку на связанные ранги.

Данные табл. 15.3, где пол — номинальная переменная, не обрабатывают с помощью по­рядковых статистик. Все изложенные выше статистики можно оценить соответствующими компьютерными программами для кросс-табуляции. Другие статистики для измерения тесно­ты связи, а именно: смешанный момент корреляции и неметрическая корреляция, обсуждают­ся в главе 17.