Закон аддитивности информации
Информационный объем сообщения - количество двоичных символов, используемое для кодирования этого сообщения.
Каждому символу в компьютере соответствует последовательность из 8 нулей и единиц, называемая байтом:
1 байт = 8 битам
Например, слово МИР в компьютере выглядит следующим образом: {М}11101101 {И}11101001 {Р}11110010.
Последовательностью нулей и единиц можно закодировать и графическую информацию, разбив изображение на точки. Если только черные и белые точки, то каждую можно закодировать 1 битом.
Используются и более крупные единицы измерения количества информации:
· 1 Кбит (килобит) = 210 бит = 1024 бит
· 1 Мбит (мегабит) = 210 Кбит = 1024 Кбит
· 1 Гбит (гигабит) = 210 Мбит = 1024 Мбит
· 1 Кбайт (килобайт) = 210 байт = 1024 байт
· 1 Мбайт (мегабайт) = 210 Кбайт = 1024 Кбайт
· 1 Гбайт (гигабайт) = 210 Мбайт = 1024 Мбайт
· 1 Тбайт (терабайт) = 210 Гбайт = 1024 Гбайт
Формула Хартли
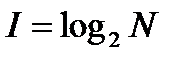
N – количество равновероятных вариантов выбора
I – количество бит информации, которое несёт каждый из вариантов
2. 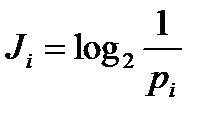 Формула Шеннона
Формула Шеннона
Ji – количество информации, которое несёт i-й вариант из N неравновероятных вариантов выбора
Рi – вероятность i-го варианта
3. 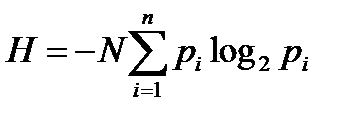 Обобщенная формула Шеннона
Обобщенная формула Шеннона
H – среднее количество информации, содержащейся в тексте из N символов n-буквенного алфавита
Средние частоты и количество информации букв русского алфавита
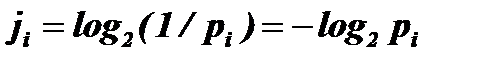
| Буквы | А | Б | В | Г | Д | Е, Ё | Ж | З |
| pi | 0.062 | 0.014 | 0.038 | 0.013 | 0.025 | 0.072 | 0.007 | 0.016 |
| ji | 4.012 | 6.158 | 4.718 | 6.265 | 5.322 | 3.796 | 7.158 | 5.966 |
| Буквы | И | Й | К | Л | М | Н | О | П |
| pi | 0.062 | 0.010 | 0.028 | 0.035 | 0.026 | 0.053 | 0.090 | 0.023 |
| ji | 4.012 | 6.644 | 5.158 | 4.837 | 5.265 | 4.238 | 3.474 | 5.442 |
| Буквы | Р | С | Т | У | Ф | Х | Ц | Ч |
| pi | 0.040 | 0.045 | 0.053 | 0.021 | 0.002 | 0.009 | 0.004 | 0.012 |
| ji | 4.644 | 4.474 | 4.238 | 5.574 | 8.966 | 6.796 | 7.966 | 6.381 |
| Буквы | Ш | Щ | Ъ, Ь | Ы | Э | Ю | Я | __ |
| pi | 0.006 | 0.003 | 0.014 | 0.016 | 0.003 | 0.006 | 0.018 | 0.175 |
| ji | 7.381 | 8.381 | 6.158 | 5.966 | 8.381 | 7.381 | 5.796 | 2.515 |
Средняя информационная ёмкость символа алфавита 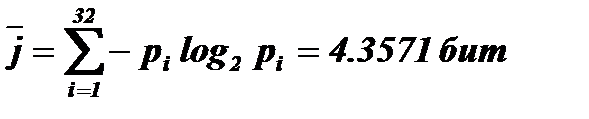
Закон аддитивности информации
Количество информации H(x1 , x2), необходимое для установления пары(x1 , x2), равно сумме количеств информации H(x1) и H(x2), необходимых для независимого установления элементов x1 , x2 H(x1 , x2) = H(x1) + H(x2)
Задание 1: Используя закон аддитивности и формулу Хартли, подсчитать, какое количество информации несет достоверный прогноз погоды.
Решение: Предположим, что прогноз погоды на следующий день заключается в предсказании дневной температуры (обычно делается выбор из 16 возможных для данного сезона значений) и одного из 4-x значений облачности (солнечно, переменная облачность, пасмурно, дождь). Тогда, H(x1 , x2) = H(x1) + H(x2) = log2 16 + log2 4 = = 4 + 2 = 6 бит Закон аддитивности информации справедлив и при алфавитном подходе к измерению информации. Для хранения двух произвольных символов одного и того же алфавита мощности N потребуется не менее
log 2 N + log 2 N = 2 log 2 N
То есть количество информации, содержащееся в сообщении, состоящем из m символов одного и того же алфавита, равно m log 2 N
Задание 2: Вычислить какой объем памяти компьютера потребуется для хранения одной страницы текста на английском языке, содержащей 2400 символов.
Решение: Мощность английского алфавита, включая разделительные знаки, N = 32. Тогда для хранения такой страницы текста в компьютере понадобится 2400 log2 32 бит = 2400 • 5 =12000 бит = 1500 байт
Задание 3: В течение 5 секунд было передано сообщение, объем которого составил 375 байт. Каков размер алфавита, с помощью которого записано сообщение, если скорость передачи составила 200 символов в секунду?
Решение: Скорость передачи равна 375 байт. 5 = 75 байт / с 75 байт / с соответствуют 200 символам / с. В одном символе содержится 75 байт ? 200 = 0,375 байт = 3 бита, то есть log 2 N = 3 бита , тогда N = 23 = 8 символов
Формула Хартли
В теории информации доказываются следующие леммы:
Лемма 1.Число различных двоичных слов длины kравно2k
Лемма 2.Множество N допускает однозначное двоичное кодирование с длинами кодов, не превосходящимиk, в том и только в том случае, когда число элементов множестваNне превосходит2k.
Согласно леммам 1 и 2, длина кода при двоичном кодировании одного символа из алфавита мощности N =2k(то есть алфавита, состоящего ровно из Nразличных символов) равна k.
Это позволяет давать эффективные оценки на минимально необходимый объем памяти компьютера для запоминания различного рода данных.
Например, кодирование сообщений на русском языке можно осуществлять с помощью алфавита, состоящего из 32 = 25различных символов (без буквы Ё). Тогда один символ при равномерном двоичном кодировании (одинаковой длине двоичного слова для каждого символа алфавита) будет занимать 5 бит памяти, а не 8 бит, как при ASCII-кодировании текстовой информации вообще.
Чтобы подсчитать объем памяти, который займет сообщение из символов такого алфавита, нужно 5 бит умножить на количество символов в сообщении.
Количество информации, которое вмещает один символ N-элементного алфавита, определяется по формулеХартли: k = log2NПо-другому, количество информации, полученное при выборе одного предмета изN равнозначных предметов, равно k = log2N
Задача 1
Рассмотрим проблему кодирования результатов голосования. Пусть имеются три варианта голосования:"за", "против" и "воздержался". Требуется закодировать результаты голосования, содержащиеся в N бюллетенях.
Применение формулы Хартли
Вопрос: Какова сложность алгоритмов сортировки, оптимальных по числу сравнений?
Ответ: Отсортировать произвольный массив с точки зрения теории информации - это значит найти одну из n!=1*2*3 ... * n перестановок всех N элементов данного массива. Сравнения элементов между собой в данном соответствуют задаваемым вопросам с возможными вариантами ответов "да" или "нет". Тогда по формуле Хартли для сортировки элементов в худшем случае потребуется получит не менее log2N! операций сравнения элементов между собой. Для оценки значения N! при больших N в математике применяют формулу Стирлинга:
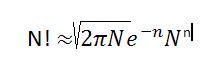
Пример 1
В задаче 1 (из предыдущего раздела) шла речь о кодировании результатов голосования. При этом каждый бюллетень содержал в себе один из трех возможных исходов голосования. Если за единицу измерения информации принять количество информации, которое можно передать одним символом трехсимвольного алфавита ("+","-","0") , что соответствует уменьшению неопределенности в три раза, то каждый бюллетень будет содержать ровно одну такую единицу информации.
Формула Шеннона
Для определения количества информации не всегда возможно использовать формулу Хартли. Её применяют, когда выбор любого элемента из множества, содержащего N элементов, равнозначен. Или, при алфавитном подходе, все символы алфавита встречаются в сообщениях, записанных с помощью этого алфавита, одинаково часто. Однако, в действительности символы алфавитов естественных языков в сообщениях появляются с разной частотой.
Пусть мы имеем алфавит, состоящий из N символов, с частотной характеристикой P1 , P2 , . . . PN , где Pi - вероятность появления i – го символа. Все вероятности неотрицательны и их сумма равна 1. Тогда средний информационный вес символа (количество информации, содержащееся в символе) такого алфавита выражается формулой Шеннона: H = P1 log2 (1/ P1) + P2 log2 (1/ P2) + . . . + PN log2 (1/ PN) где H – количество информации, N – количество возможных событий, Pi – вероятность отдельных событий
Энтропия - мера внутренней неупорядоченности информационной системы. Энтропия увеличивается при хаотическом распределении информационных ресурсов и уменьшается при их упорядочении.
Энтропия термодинамической системы определяется как натуральный логарифм от числа различных микросостояний Z, соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией)
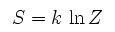
Коэффициент пропорциональности k и есть постоянная Больцман
Экономное кодирование
Сведения о вероятности появления различных символов в сообщении могли бы сделать кодирование гораздо более экономным.
Рассмотрим пример:
Сообщение о том, что бутерброд упал маслом вниз несет в себе менее 1 бита информации. Но, как известно, со стола бутерброд падает маслом вниз почти всегда. И даже в том случае, если м будем бросать будерброд несколько раз, а результаты экспериментов будем записывать символами 0 и 1, то и в среднем один символ полученного двоичного кода будет нести менее одного бита информации в среднем.
Вывод: Кодирование с учетом появления различных символов в сообщении можно сделать более экономным, чем кодирование, осуществленное в предположении равной частоты их появления.
Практический пример экономного кодирования. Зная приблизительные частоты, с которыми встречаются буквы русского алфавита (Табл.1), можно более точно, чем при использовании алфавитного подхода, не учитывающего вероятности появления различных символов, ответить на вопрос, сколько информации несет то, или иное слово (или, к примеру, чью-нибудь фамилию).

Для кодирования фамилий мы можем использовать 32-символьный алфавит (приравняв значения букв "Е" и "Ё"). Для кодирования алфавита состоящего из 32 символов достаточно 5 бит ( 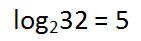 ).
).
К примеру, фамилия Белов несет в себе 25 бит информации согласно алфавитному подходу. С учетом частоты появления русских букв и закона аддитивности информации информативность этой же фамилии равна 23 битам.
Можно использовать другой подход к измерению информации, если отдельно кодировать корни фамилий и их окончания. Тогда можно обойтись меньшим количеством бит. Так, окончание "ов" встречается как минимум в половине мужских русских фамилий, и согласно нашему подходу, будет нести в себе один бит информации. Корень "Бел" встречается, к примеру, один раз на 128 фамилий, следовательно для его кодирования необходимо 7 бит. Тогда общий код фамилии "Белов" теоритически может занимать всего лишь один байт!
Далее: практические задания по теме, энтропия, свойства энтропии с доказательствами
Задания:
1. Вычислить какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков.
Решение: Всего шариков 10 + 20 +30 +40 = 100 Вероятности сообщений о цвете следующие: Рб = 10/100 =0,1; Рк = 20/100 =0,2; Рс = 30/100 =0,3; Рз = 40/100 =0,4 События не равновероятны, поэтому воспользуемся формулой Шеннона: N H=- ? Pi log 2Pi = - (0,1• log2 0,1+ 0,2• log2 0,2+ 0,3• log2 0,3+ 0,4• log2 0,4) бит i=1
2. Вычислить какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке хранятся 30 белых, 30 красных, 30 синих и 10 зеленых шариков.
Решение: Всего шариков 30 + 30 +30 +10 = 100 Вероятности сообщений о цвете следующие: Рб = Рк = Рс = 30/100 =0,3; Рз = 10/100 =0,1 События не равновероятны, поэтому воспользуемся формулой Шеннона: N H=- ? Pi log 2Pi = - (3 • 0,3• log2 0,3+ 0,1• log2 0,1) бит i=1 Ответ: ? бита
3. Вычислить какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке хранятся 25 белых, 25 красных, 25 синих и 25 зеленых шариков.
Решение:Всего шариков 25 + 25 +25 +25 = 100 Вероятности сообщений о цвете следующие: Рб = Рк = Рс = Рз = 25/100 =1/4 События не равновероятны, поэтому воспользуемся формулой Шеннона: N H = - ? Pi log 2Pi = - (4 • 1/4• log2 1/4) = - (4 • 1/4• (-2)) = 2 бита i=1 Ответ: 2 бита
Единицы энтропии
Полученная Шенноном формула позволила вывести единицы измерения количества информации. Для этого приравняем выражение для энтропии системы к единице:
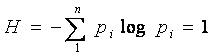
Какие переменные входят в это выражение:
1. Число возможных состояний системы n
2. Основание логарифма a
3. Распределение вероятностей pi
Для решения уравнения необходимо задаться из каких-либо соображений двумя переменными и вычислить третью.
БИТ
Рассмотрим физическую систему с двумя равновероятными состояниями. Количество информации равное единице может быть получено, если в формуле Шеннона и взять логарифм по основанию 2. Пусть n=2 и , тогда 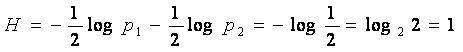
Следовательно, в данном случае единицей энтропии служит энтропия системы с двумя равновероятными состояниями, вычисленная с помощью логарифма с основанием два. Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита. Название bit образовано из двух начальных и последней букв английского выражения binary unit, что значит двоичная единица
Другими словами, если мы приняли, что информация – это устраненная неопределенность, тогда в случае неопределенности физической системы с двумя равновероятными состояниями выбор будет производиться между двумя взаимоисключающими друг друга равновероятными сообщениями, например, между двумя качественными признаками: положительным и отрицательным импульсами, импульсом и паузой и т.п. Количество информации, переданное в этом простейшем случае, принято за единицу количества информации - бит. Бит является единицей количества информации и представляет собой информацию, содержащуюся в одном дискретном сообщении источника равновероятных сообщений с объемом алфавита равного двум.
ДИТ
Возьмем основание логарифма равным 10-ти и рассмотрим физическую систему с числом n равновероятных состояний. Определим, чему должна быть равна переменная n, чтобы количество информации в формуле Шеннона было равно единице, когда взят логарифм по основанию 10:
Пусть а=10 и 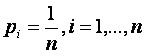
Тогда 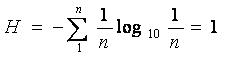
Поскольку отсюда следует, что , тогда число состояний n=10. Итак, дит – это энтропия системы с десятью равновероятными состояниями, вычисленная с помощью логарифма с основанием десять.
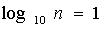
Можно заметить, что основание логарифма равно числу состояний. Это – важное замечание! Перейдем теперь к рассмотрению виртуальной системы с количеством состояний, равным натуральной единице е. Дит - единица количества информации, содержащейся в одном дискретном сообщении источника равновероятных сообщений с объемом алфавита, равного десяти.
НИТ
Если взять физическую систему с е состояниями, получим натуральную единицу количества информации, называемую нитом, при этом основание логарифма в формуле Шеннона равно е=2,7.
Взаимосвязь между единицами количества информации:
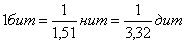
Свойства энтропии
Свойство 1
Неопределенность физической системы равна нулю: H = H(p1, p2, …, pn) = 0, если одно из чисел p1, p2, …, pn равно 1, а остальные равны нулю.
Доказательсто:
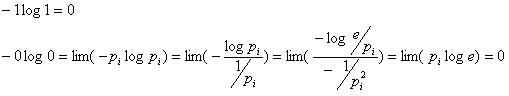
Свойство 2
Энтропия максимальна, когда все состояния источника равновероятны.
Доказательство:
Введем ограничение на : 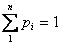
Ищем локальный экстремум. Для этого рассмотрим функционал
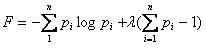 ,где
,где 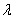 по Лагранжу,
по Лагранжу,
а 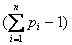 - из условия ограничения.
- из условия ограничения.
Берем первые частные производные по 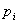 ::
::
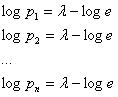
Поскольку правые части всех выражений одинаковые, можно сделать вывод о равновероятных состояниях физической системы, то есть:
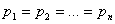 ,
,
Тогда:
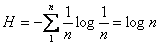
Получили выражение для максимальной энтропии, соответствующее формуле Хартли.
Свойство 3
Всякое изменение вероятностей p1, p2, …, pn в сторону их выравнивания увеличивает энтропию H(p1, p2, …, pn).
Доказательство:
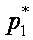 ,
,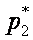

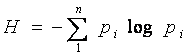 и
и 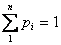
Пусть 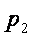 >
> 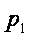 , тогда
, тогда 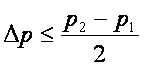 ,
,
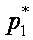 +
+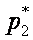 +…+
+…+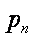
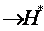
Нам нужно доказать, что 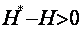
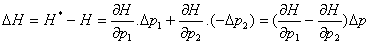
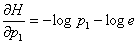 и
и 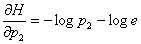
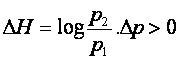 , так как
, так как 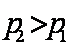 , что и требовалось доказать.
, что и требовалось доказать.
Свойство 4
Математическое ожидание вероятности есть энтропия (Без доказательства) 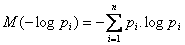
Код Хаффмана
Оптимальное кодирование информации.Важной задачей современной информатики является кодирование информации наиболее коротким способом. На сегодняшний день разработаны универсальные способы кодирования информации, например, алгоритм Хаффмана (1952 год), который является простым, быстрым и оптимальным. В основу алгоритма Хаффмана положена идея: кодировать более коротко те символы, которые встречаются чаще, а те, которые встречаются реже кодировать длиннее. При этом возникает проблема: как понять, где кончился код одного символа и начался код другого? Эту проблему можно решать двумя способами:
1. Закодированная последовательность имеет вид {длина кода, код} {длина кода, код} … {длина кода, код}
2.Строится так называемый префиксный код: в нем не требуется указывать длину кода, но коды получаются несколько длиннее. Код Хаффмана является префиксным.
· Определение:Префиксный код – это код, в котором код одного символа не может быть началом кода другого символа.
Задание:Построить код Хаффмана для алфавита, состоящего из 5-ти символов a, b, c, d, e с частотами (вероятностями появления в тексте) 0,37 (a); 0,22 (b); 0,16 (c); 0,14 (d); 0,11 (e)
Решение:Объединим символы d, e (символы с наименьшими частотами), тогда частота символа de равна 0,14 (d) + 0,11 (e) = 0,25 (de) , получаем новые частоты 0,37 (a); 0,22 (b); 0,16 (c); 0,25 (de) Объединим символы a, de (символы с наибольшими частотами), тогда частота символа ade равна 0,37 (a) + 0,25 (de) = 0,62 (ade), получаем новые частоты 0,62 (ade); 0,22 (b); 0,16 (c) Объединим символы b, c (символы с наименьшими частотами) , тогда частота символа bc равна 0,22 (b) + 0,16 (c) = 0,38 (bc), получаем новые частоты 0,62 (ade); 0,38 (bc) Сопоставим ade код 0 , bc - код 1 (Символу с большей частотой - более короткий код) Расщепим символ ade на символы a и de с кодами 00 и 01 Расщепим символ bc на символы b и с с кодами 10 и 11 Расщепим символ de на символы d и e с кодами 010 и 011
 Ответ:Коды исходного алфавита a, b, c, d, e следующие: 00 (a); 10 (b); 11 (c); 010 (d); 011 (e) Полученный код – префиксный, код каждого символа не является началом кода другого символа. Однако, определить, что построенный код для конкретной последовательности – минимальный, нельзя.
Ответ:Коды исходного алфавита a, b, c, d, e следующие: 00 (a); 10 (b); 11 (c); 010 (d); 011 (e) Полученный код – префиксный, код каждого символа не является началом кода другого символа. Однако, определить, что построенный код для конкретной последовательности – минимальный, нельзя.
Это не означает, что ни для какого объекта минимальную последовательность построить нельзя. А означает, что часто невозможно доказать минимальность построенной последовательности.
