Ростов & Орёл & Курск

Пирожное | выпечка

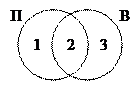Решение (вариант 1, рассуждения по диаграмме):

1) построим диаграмму Эйлера-Венна, обозначив области «пирожное» (через П) и «выпечка» (В) :

2) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

3) несложно сообразить, что число сайтов в интересующей нас области равно

N₁ + N₂ + N₃ = (N₁ + N₂) + (N₃ + N₂) – N₂

4) поскольку нам известно, что по условию

N₁ + N₂ = 8700

N₃ + N₂ = 7500

N₂ = 3200

сразу получаем

N₁ + N₂ + N₃ = 8700 + 7500 - 3200 = 13000

5) таким образом, ответ – 13000.

Решение (вариант 2, общая формула):

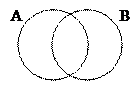
1) сначала выведем формулу, о которой идет речь; построим диаграмму Эйлера-Венна для двух переменных A и B:

2) обозначим через N_A, N_B, N_A&B и N_A|B число страниц, которые выдает поисковый сервер соответственно по запросам A, B, A & B и
A | B

3) понятно, что если области A и B не пересекаются, справедлива формула N_A|B=N_A+N_B

4) если области пересекаются, в сумму N_A+N_B область пересечения N_A&B входит дважды, поэтому в общем случае

N_A|B = N_A + N_B - N_A&B

5) в данной задаче

N_П = 8700, N_В = 7500, N_П&В = 3200

6) тогда находим число сайтов в интересующей нас области по формуле

N_П|B = N_П + N_B – N_П&B = 8700 + 7500 – 3200 = 13000

7) таким образом, ответ – 13000.

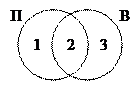Решение (вариант 3, решение системы уравнений):

1) нарисуем области «пирожное» (обозначим ее через П) и «выпечка» (В) в виде диаграммы (кругов Эйлера); при их пересечении образовались три подобласти, обозначенные числами 1, 2 и 3;

2) составляем уравнения, которые определяют запросы, заданные в условии:

пирожное & выпечка N₂ = 3200

пирожное N₁ + N₂ = 8700

выпечка N₂ + N₃ = 7500

3) подставляя значение N₂ из первого уравнения в остальные, получаем

N₁ = 8700 - N₂ = 8700 – 3200 = 5500

N₃ = 7500 - N₂ = 7500 – 3200 = 4300

4) количество сайтов по запросу пирожное | выпечка равно

N₁ + N₂ + N₃ = 5500 + 3200 + 4300 = 13000

5) таким образом, ответ – 13000.

2 . В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Количество страниц (тыс.)
США | Япония | Китай
Япония | Китай
(США & Япония) | (США & Китай)

Сколько страниц (в тысячах) будет найдено по запросу

США

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

1) заметим, что в силу тождества последний запрос в таблице равносилен такому:

(США & Япония) | (США & Китай) Û США & (Япония | Китай)

2) тогда вводя обозначение для областей

A = США, B = Япония | Китай,

получаем стандартную задачу с двумя переменными:

Запрос	Количество страниц (тыс.)
А | B
B
А & B
А	?

3) имеем по формуле (см. решения ниже)

N_A = N_A|B - N_B + N_A&B = 450 – 260 + 50 = 240

4) Ответ: 240

3. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Количество страниц (тыс.)
Ростов & (Орёл & Курск | Белгород)
Ростов & Белгород
Ростов & Орёл & Курск & Белгород

Сколько страниц (в тысячах) будет найдено по запросу

Ростов & Орёл & Курск

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

1) заметим, что во всех четырёх запросах есть «сомножитель» «Ростов &», поэтому эта задача равносильна такой:

Запрос	Количество страниц (тыс.)
Орёл & Курск | Белгород
Белгород
Орёл & Курск & Белгород
Орёл & Курск	?

2) теперь обозначим A = Орёл & Курск и получим задачу с двумя областями:

Запрос	Количество страниц (тыс.)
A | Белгород
Белгород
A & Белгород
A	?

3) по формуле для задачи с двумя областями (см. задачи, разобранные ниже)

N_A|B = N_A + N_B - N_A&B

получаем

N_A = N_A|B - N_B + N_A&B

4) вычисляем: 370 – 204 + 68 = 234.

5) Ответ: 234.

4. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Количество страниц (тыс.)
Ухо
Подкова
Наковальня
Ухо | Подкова | Наковальня
Ухо & Наковальня
Ухо & Подкова

Сколько страниц (в тысячах) будет найдено по запросу

Подкова & Наковальня

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение (вариант 1, рассуждения по диаграмме):

1) построим диаграмму Эйлера-Венна

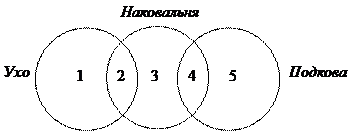
2) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

3) здесь 5 областей, причём известны следующие данные:

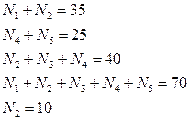
4) нас интересует область 4. Находим ответ прямой подстановкой:

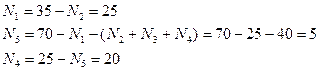
5) таким образом, ответ – 20.

5. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

Ключевое слово	Количество сайтов, для которых данное слово является ключевым
Сканер
Принтер
Монитор

Сколько сайтов будет найдено по запросу