Правила выполнения запросов

В каждой поисковой системе в разделе Помощь (Help) можно получить сведения о том, как искать, как составить строку запроса. Ниже приведена информация о типовом, "усредненном" языке запросов.

Простой запрос. Ввести одно слово, определяющее тему поиска. Например, в поисковой системе Rambler.ru достаточно ввести: автоматика.

Находятся документы, в которых встречаются слова, указанные в запросе. Распознаются все формы слов русского языка, как правило, регистр букв игнорируется.

В запросе можно использовать символ "*" или "?". Знаком "?" в ключевом слове заменяется один символ, на место которого может быть подставлена любая буква, а знаком "*" – последовательность символов. Например, запрос автомат * позволит найти документы, включающие слова автоматический, автоматика и т.д.

Сложный запрос. Часто возникает необходимость комбинирования ключевых слов для получения более определенной информации. В этом случае используются дополнительные слова-связки, функции, операторы, символы, комбинации операторов, разделенные скобками.

Например, запрос музыка & (beatles | битлз) означает, что пользователь ищет документы, содержащие слова музыка и beatles или музыка и битлз. В таблице 2 приведены правила формирования запросов, принятые в системе Апорт

(http://www.aport.ru).

Таблица 2 – Операторы для формирования запросов

Оператор	Синонимы	Комментарий
И	AND &	По запросу будут найдены документы, содержащие оба ключевых слова. Его можно и не писать. Например, запрос: информатика и учебник эквивалентен информатика учебник
ИЛИ	OR |	Производится поиск тех документов, в которых используется любое из указанных слов или оба слова одновременно
НЕ	NOT - ~	Поиск ограничивается документами, не содержащими слово, указанное после оператора
" "	' '	Двойные или одинарные кавычки позволяют находить словосочетание
Дата=	дата: date=	Поиск ограничивается документами, попадающими в заданный интервал дат. Пример 1. валюта дата=01/02/2002–01/03/2002. По этому запросу будут выданы документы, содержащие слово "валюта" и имеющие дату от 1 февраля 2002 г. до 1 марта 2002 г. Пример 2.date=01/03/2002 валюта Пример 3. дата:<02/03/2002 валюта

ЦЕЛЬ РАБОТЫ

1.1. Изучить приемы простых вычислений с использованием программы MathCad.

1.2. Изучить приемы решения уравнений с использованием программы MathCad.

ПРИБОРЫ И ОБОРУДОВАНИЕ

2.1. ПЭВМ IBM PC.

2.2. Математический пакет MathCAD.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

3.1. Изучить теоретические сведения (Приложение А).

3.2. Выполнить задания (Приложение Б).

3.3. Ответить на контрольные вопросы.

3.4. Оформить отчет, сделать выводы о проделанной работе.

4. Содержание отчёта:

4.1. Тема работы.

4.2. Цель работы.

4.3. Приборы и оборудование.

4.4. Выполнение работы.

4.5. Выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

5.1. С помощью какого оператора можно вычислить выражение?

5.2. Как вставить текстовую область в документ MathCad?

5.3. Чем отличается глобальное и локальное определение переменных? С помощью каких операторов определяются?

5.4. Какие системные (предопределенные) переменные Вам известны? Как узнать их значение?

5.5. Какие виды функций в MathCad Вам известны?

5.6. С помощью каких операторов можно вычислить интегралы, производные, суммы и произведения?

5.7. Опишите структуру блока решения уравнений.

5.8. Что необходимо для решения системы уравнений в пакете MathCAD?

5.9. Опишите структуру блока решения системы уравнений.

5.10. Какие выражения недопустимы внутри блока решения системы уравнений?

Теоретические сведения

Основы работы с MathCAD

MathCAD работает с документами. С точки зрения пользователя, документ - это чистый лист бумаги, на котором можно размещать блоки трех основных типов: математические выражения, текстовые фрагменты и графические области.

Расположение нетекстовых блоков в документе имеет принципиальное значение – слева направо и сверху вниз.

Математические выражения

К основным элементам математических выражений MathCAD относятся типы данных, операторы, функции и управляющие структуры.

Операторы

Операторы - элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д.

Оператор определяет:

- действие, которое должно выполняться при наличии тех или иных значений операндов;

- сколько, где и какие операнды должны быть введены в оператор.

Операнд – число или выражение, на которое действует оператор. Например, в выражении 5! + 3 число 3и выражение 5!– операнды оператора + (плюс), а число 5 операнд оператора факториал (!). После указания операндов операторы становятся исполняемыми по документу блоками. В Приложении А данной работы приведен список наиболее часто используемых операторов.

Типы данных

К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа.

Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в MathCAD представляют собой набор латинских или греческих букв и цифр.

В MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения (см. Приложение С). Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Options команды Математика Þ Опции.

Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной.

Если переменной присваивается начальное значение с помощью оператора :=, вызывается нажатием клавиши :(двоеточие) на клавиатуре, такое присваивание называется локальным. До этого присваивания переменная не определена и ее нельзя использовать. Однако с помощью знака º (клавиша ~на клавиатуре) можно обеспечить глобальное присваивание (см. Пример 1 Рисунка 1). MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все действия, предписанные локальным оператором присваивания (º), а при втором – производятся действия, предписанные локальным оператором присваивания (:=), и отображаются все необходимые результаты вычислений (=).

Существуют также жирный знак равенства = (комбинация клавиш Ctrl +=), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства ® (комбинация клавиш Ctrl + .).

Рисунок 1. Математические выражения

Функции

Функция – выражение, согласно которому проводятся некоторые вычисления с аргументами, и определяется его числовое значение.

Следует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции (см. Пример 2 Рисунка 1).

Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение.

Функции в пакете MathCAD могут быть встроенные (см. Приложение 3), т. е. заблаговременно введенные разработчиками, и определенные пользователем.

Способы вставки встроенной функции:

Выбрать пункт меню Вставка Þ Функция.

Нажать комбинацию клавиш Ctrl + E.

Щелкнуть на кнопке .

Текстовые фрагменты

Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов:

- текстовая область предназначена для небольших кусков текста - подписей, комментариев и т. п. Вставляется с помощью команды Вставка Þ Текстовая регионили комбинации клавиш Shift + " (двойная кавычка);

- текстовый абзац применяется в том случае, если необходимо работать с абзацами или страницами. Вставляется с помощью комбинации клавиш Shift + Enter.

Решение уравнений средствами MathCad

Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Однако такие уравнения могут решаться численными методами с заданной точностью (не более значения заданного системной переменной TOL).

Численное решение нелинейного уравнения

Для простейших уравнений вида f(x) = 0 решение в MathCad находится с помощью функции root (Рисунок 2).

root( f(х1, x2, …), х1, a, b )

Возвращает значение х1, принадлежащее отрезку [a, b], при котором выражение или функция f(х)обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.

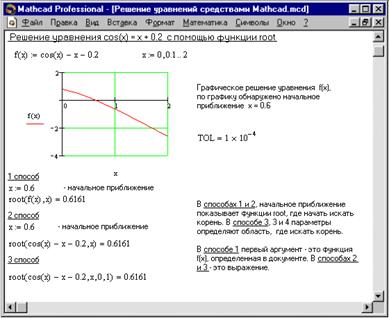
Рисунок 2 – Решение уравнений средствами Mathcad.

Аргументы:

f(х1, x2, …) -функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

х1 –имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. MathCad использует его как начальное приближение при поиске корня.

a, b –необязательны, если используются, то должны быть вещественными числами, причем a < b.

Приближенные значения корней (начальные приближения) могут быть:

- Известны из физического смысла задачи.

- Известны из решения аналогичной задачи при других исходных данных.

- Найдены графическим способом.

Наиболее распространен графический способ определения начальных приближений. Принимая во внимание, что действительные корни уравнения f(x) = 0 - это точки пересечения графика функции f(x) с осью абсцисс, достаточно построить график функции f(x) и отметить точки пересечения f(x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню

Отсутствие сходимости функции root

Если после многих итераций MathCad не находит подходящего приближения, то появится сообщение (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:

- Уравнение не имеет корней.

- Корни уравнения расположены далеко от начального приближения.

- Выражение имеет локальные max и min между начальным приближением и корнями.

- Выражение имеет разрывы между начальными приближениями и корнями.

- Выражение имеет комплексный корень, но начальное приближение было вещественным.

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться.

Рекомендации по использованию функции root

Для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида 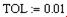Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика Þ Параметры… Þ Переменные Þ Допуск сходимости (TOL).

Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их.

Если функция f(x) имеет малый наклон около искомого корня, функция root(f(x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x) = 0 на g(x) = 0

.

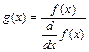Для выражения f(x) с известным корнем а, нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x) = f(x)/(x ‑ a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения f(x) = 0, выбирая различные начальные приближения.

Решение систем уравнений

MathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.

Для решения системы уравнений необходимо выполнить следующее:

- Задать начальное приближение для всех неизвестных, входящих в систему уравнений. MathCad решает систему с помощью итерационных методов.

- Напечатать ключевое слово Given. Оно указывает MathCad, что далее следует система уравнений.

- Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, ³ и £.

- Введите любое выражение, которое включает функцию Find, например: а:= Find(х, у).

Find(z1, z2, . . .)

Возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое–либо выражение, содержащее функцию Find, называют блоком решения уравнений.

Следующие выражения недопустимы внутри блока решения:

- Ограничения со знаком ¹.

- Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.

- Неравенства вида a < b < c.

Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find.

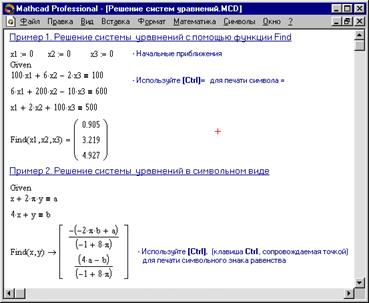
Рисунок 3. Решение систем уравнений в MathCAD.

Сообщение об ошибке (Решение не найдено) при решении уравнений появляется, когда:

- Поставленная задача может не иметь решения.

- Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот.

- В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Для поиска искомого решения нужно задать различные начальные приближения.

- Возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL. Пример 1 Рисунка 3 иллюстрирует решение системы уравнений в MathCAD.

Встроенные операторы

В таблице, приведенной ниже, используются следующие обозначения: Xи Y - переменные или выражения любого типа; x и y- вещественные числа; zи w- вещественные или комплексные числа; m и n- целые числа; A и B- массивы (векторы или матрицы); i - дискретный аргумент; t- любая переменная; f- любая функция.

Оператор	Клавиши	Назначение оператора
X := Y	X : Y	Локальное присваивание X значения Y
X ºY	X ~ Y	Глобальное присваивание X значения Y
X =	X =	Вывод значения X
X + Y	X + Y	Сложение X с Y
X + Y	X [Ctrl][¿] Y	То же, что и сложение. Перенос чисто косметический.
X - Y	X - Y	Вычитание из X значения Y
X × Y	X * Y	Умножение X на Y
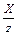	X / z	Деление X на z
zw	z ^ w	Возведение z в степень w
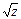	z \	Вычисление квадратного корня из z
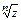	n [Ctrl]\ z	Вычисление корня n-ой степени из z
n !	n !	Вычисление факториала
Bn	B [ n	Ввод нижнего индекса n
An,m	A [ n , m	Ввод двойного индекса
A<n>	A [Ctrl]6 n	Ввод верхнего индекса
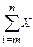	[Ctrl][Shift]4	Суммирование Х по i = m, m + 1, . . . n
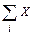	$	Суммирование Х по дискретному аргументу i
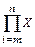	[Ctrl][Shift]3	Перемножение Х по i = m, m + 1, . . . n
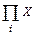	#	Перемножение Х по дискретному аргументу i
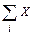	$	Суммирование Х по дискретному аргументу i
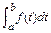	&	Вычисление определенного интеграла f(t) на интервале [a, b]
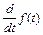	?	Вычисление производной f(t) по t
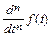	[Ctrl]?	Вычисление производной n-го порядка функции f(t) по t
(§)	‘	Ввод пары круглых скобок с шаблоном
x > y	x > y	Больше чем
x < y	x < y	Меньше чем
x ³ y	x [Ctrl]0y	Больше либо равно
x £ y	x [Ctrl]9y	Меньше либо равно
z =w	z [Ctrl]=w	Булево равенство возвращает 1, если операнды равны, иначе 0
z ¹ w	z [Ctrl]3w	Не равно
|z|	| z	Вычисление модуля комплексного z

Встроенные функции