Хранение изображений в компьютере
Все цифровые устройства работы с цветом хранят, обрабатывают и воспроизводят цвет и цветные изображения с помощью значений RGB. Для того чтобы сохранить цифровое изображение, его сначала требуется разбить на сетку мелких пикселей (точек). Каждый пиксель замеряется на количество в нем красного, зеленого и синего цветов. Затем все изображение в целом записывается пиксель за пикселем. Для хранения изображения площадью 3 квадратных дюйма с разрешением 150 точек на дюйм требуется 202.500 пикселей или 607.500 байт.
Часто теоретическую модель, описывающую принцип хранения цветов в компьютере, представляют в виде куба. Этот метод прекрасно зарекомендовал себя, позволяя с легкостью переключаться между различными цветовыми моделями, включая цветовой круг, схему CIE, схему HSV, сферу Мюнселя, систему Pantone, стандарт цветов DIN и карту цветов спектрального свечения.
Фундаментальное отличие COLORCUBE от всех других моделей состоит в том, что куб описывает цвета в цветовом пространстве, основываясь на входных параметрах (на количестве основных пигментных цветов, используемых для создания смешанного цвета). Другие же модели базируются на измерении выходных параметров (т.е. на том, как выглядит результирующий цвет). Система цветов, основанная на входных параметрах, значительно облегчает решение вопросов с наименованием цветов, из воспроизведением, выводом, калибрацией, обработкой и преобразованием в другие цветовые схемы.
Представление цветовой гаммы
Возможность представить все существующие цвета в виде трехмерной цветовой гаммы и видеть их взаимосвязь друг с другом дает огромное преимущество при работе с цветом. Хотя уже и существуют несколько компьютерных моделей, отображающих теоретически цветовую гамму, модель COLORCUBE первая в своем роде физическая модель, в которой видимы все внутренние цвета.
Человеческий глаз способен видеть более 16 миллионов оттенков цветов. Ключевое свойство COLORCUBE состоит в том, что сначала определяются внешние точки куба, а затем определяются цвета и оттенки между этими ключевыми точками. Таким образом, определяя крайние границы цветовой гаммы, мы получаем также возможность видеть и промежуточные цвета. Задавая общее количество требуемых цветов, мы можем генерировать кубы любой плотности. Например, COLORCUBE который определяет все воспроизводимые цвета будет иметь в каждой грани 256 кубиков, то есть состоять из 16,777,216 кубиков.

Цветовые плоскости в трехмерном цветовом пространстве
Смешивание цветов
Каждый цветовой элемент в COLORCUBE имеет уникальный цифровой идентификатор, указывающий на то, в какой пропорции были использованы исходные значения для воспроизведения данного цвета. Каждый элемент так же имеет свое уникальное местоположение внутри куба. Таким образом образуется связь между информацией о положении и информацией о способе смешении цветов для данного элемента.
Если дана информация о смешении цветов, мы всегда сможем вычислить где в кубе расположен данный элемент. Если дано расположение элемента, мы можем вычислить в какой пропорции надо смешивать основные цвета, чтобы получить цвет данного элемента. Используя это свойство COLORCUBE нам не нужно уже больше гадать по поводу названий цветов, их описаний и параметров смешения. Теперь мы можем быть точно уверенны в том, что определенный нами цифровой цвет всегда можно будет воспроизвести в данной гамме и что это будет один и тот же цвет.
Выбор цвета
Уникальное трехмерное расположение цветов в модели COLORCUBE прекрасно подходит для инструментов выбора цвета. С помощью куба запросто можно определять дополнительные цвета, гармоничные комбинации, подбирать теплые и холодные цвета, находить ненасыщенные цвета, их оттенки, цвета с одинаковыми значениями. Становится ясным, что все взаимосвязи между цветами носят математический характер, и эти взаимосвязи можно смоделировать с помощью простой математики в декартовых координатах XYZ.
Манипуляции с цветом
Для манипуляции с цветами в цветовой гамме необходимо определить набор математических правил, с помощью которых будут меняться цвета. Математика цвета (статья о ней будет переведена позже) разбивает цвет на составляющие основные цвета а затем проводит с ними математические операции. В результате выводятся формулы смешивания для получения любого нового цвета, выбранного с COLORCUBE.
Например, для того, чтобы предсказать результат смешения двух цветов, разложите каждый цвет на составляющие его основные цвета. Затем, сложите одинаковые основные цвета. В результате получаются координаты, по которым в COLORCUBE можно найти получаемый цвет. Та же логика применяется и к вычитанию цветов (вычитанию одного цвета из другого), а также к таким более сложным операциям как регулировка контраста, яркости и насыщенности.
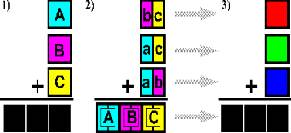
Математика цвета в гамме субтрактивных цветов:
I. Равное количество циана, фуксина и желтого (ABC) дает черный (K)
II. Потому что:
1. Равные количества фуксина и желтого дают красный
2. Равные количества циана и желтого дают зеленый
3. Равные количества циана и фуксина дают синий
4. Равные количества красного, зеленого и синего дают черный
