Методические указания к выполнению задания 1
По пункту I. Полученная в результате наблюдений информация о значениях случайной величины (доремонтный ресурс отверстия или сопряжений втулка – палец) представляется в виде вариационного ряда, т.е. в порядке возрастания абсолютной величины ресурса. Составление вариационного ряда является первым этапом статистической обработки результатов наблюдений. При этом отдельные значения случайной величины предоставляются в упорядоченном виде.
Для более полной картины изменения случайной величины составляется статистический ряд или ряд распределения.
Общая схема составления ряда распределения состоит в следующем: случайная величина (в нашем примере ресурс Тдр) принимает различные значения. Каждое из этих значений имеет определенную частоту (повторяемость) m1,m 2,m3,...,mn , а также частость (опытную вероятность) Pопi = 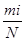 , где N- общее число значений случайной величины. Таким образом, ряд распределения характеризует соотношение между возможными значениями случайной величины и соответствующими этим значениям частотами и частостями (опытными вероятностями). Ряд распределения может быть представлен в виде таблицы, графика или аналитической форме.
, где N- общее число значений случайной величины. Таким образом, ряд распределения характеризует соотношение между возможными значениями случайной величины и соответствующими этим значениям частотами и частостями (опытными вероятностями). Ряд распределения может быть представлен в виде таблицы, графика или аналитической форме.
Для построения ряда распределения информация разбивается на К интервалов. Количество интервалов обычно принимается от 5 до 15. Каждый интервал имеет верхнюю и нижнюю границу. Далее определяют, какое число значений случайной величины (из общего числа N) попадает в отдельные интервалы, устанавливая тем самым частоты mi по интервалам. Затем находят для каждого интервала величину отношения 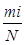 - частость. Если, например, студенту задан вариант 1 (см. приложение Б), то он должен составить ряд распределения ресурса по 5 интервалам от 0,5 до 5,5 тыс. часов. При этом следует иметь в виду, что для определения частоты mi в каждый интервал включаются те значения, которые численно больше нижней границы, но меньше или равны верхней границе интервала. Например, значение 3500 ч. входит в интервал 2,5-3,5 тыс. ч, а значение 2500 ч – в интервал 1,5-2,5 тыс. ч.
- частость. Если, например, студенту задан вариант 1 (см. приложение Б), то он должен составить ряд распределения ресурса по 5 интервалам от 0,5 до 5,5 тыс. часов. При этом следует иметь в виду, что для определения частоты mi в каждый интервал включаются те значения, которые численно больше нижней границы, но меньше или равны верхней границе интервала. Например, значение 3500 ч. входит в интервал 2,5-3,5 тыс. ч, а значение 2500 ч – в интервал 1,5-2,5 тыс. ч.
Для примера в таблице 1 приведен ряд распределения ресурса отверстия (см. табл. 1 приложение А) для варианта 29.1(см. приложение Б).
При составлении соответствующего ряда распределения необходимо учитывать, что сумма частот по интервалам должна быть равна общему числу значений ресурса, т.е. 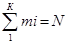 , а сумма частостей должна быть равна единице, т.е.
, а сумма частостей должна быть равна единице, т.е. 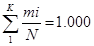 . При составлении таблицы 1 необходимо определить также величину накопленных частостей (опытных вероятностей) для каждого интервала, т.е. ∑Pопi
. При составлении таблицы 1 необходимо определить также величину накопленных частостей (опытных вероятностей) для каждого интервала, т.е. ∑Pопi 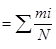 . Представленный в таблице 1 ряд распределения ресурса отверстия, показывает, что абсолютное большинство значений Тдр попали во 2 и 3 интервалы (46 из 70). Поэтому с вероятностью 0,66 (см.
. Представленный в таблице 1 ряд распределения ресурса отверстия, показывает, что абсолютное большинство значений Тдр попали во 2 и 3 интервалы (46 из 70). Поэтому с вероятностью 0,66 (см. 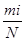 2-го и 3-го интервалов 0,400+0,260=0,66) можно утверждать, что ресурс отверстия будет не меньше 1600 ч. и не больше 3400 ч. Такая предварительная, оценка ресурса отверстия может быть дана уже при анализе статистического ряда распределения.
2-го и 3-го интервалов 0,400+0,260=0,66) можно утверждать, что ресурс отверстия будет не меньше 1600 ч. и не больше 3400 ч. Такая предварительная, оценка ресурса отверстия может быть дана уже при анализе статистического ряда распределения.
Таблица1 – Расчет показателей
| Частичные интервалы Тдр,тыс.ч. | 0,7… 1,6 | 1,6… 2,5 | 2,5…3,4 | 3,4…4,3 | 4,3…5,2 | 5,2…6,1 | - |
| Середины интервалов Тci,тыс.м-ч | 1,15 | 2,05 | 2,95 | 3,85 | 4,75 | 5,65 | - |
| Частоты mi | 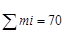 | ||||||
Частости Pопi = 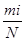 | 0,100 | 0,400 | 0,260 | 0,142 | 0,070 | 0,028 | 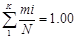 |
Накопленные частости 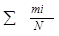 | 0,100 | 0,500 | 0,760 | 0,902 | 0,972 | 1,000 | - |
По пункту 2. Статистический ряд распределения ресурса более наглядно может быть представлен графически в виде гистограммы и полигона (см. рис.1). При построении гистограммы на горизонтальной оси графика откладывают значения, соответствующие границам частичных интервалов, а на вертикальной – частоты или частости по этим интервалам, в соответствии с данными табл.1. В результате построения получается ступенчатый многоугольник, или гистограмма.
Если теперь соединить прямыми линиями середины верхних сторон прямоугольников, образующих гистограмму, то получим полигон распределения в виде ломаной линии, характеризующей плотность распределения значений случайной величины.
Пример построения гистограммы и полигона распределения ресурса для варианта 29.1 согласно табл.1 приведен на рисунке 1.
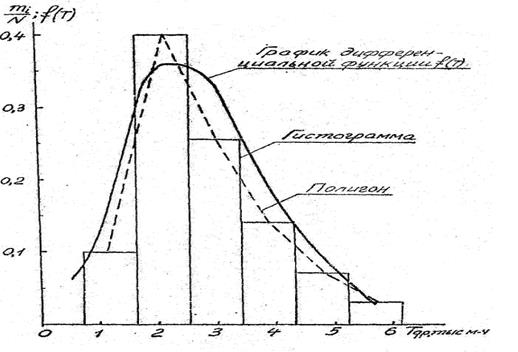
Рисунок 1 - Гистограмма, полигон и дифференциальная функция распределения доремонтного ресурса отверстия под подшипник коробки скоростей станка
Наиболее распространенной характеристикой распределения ресурса (как и любой случайной величины) является интегральная функция распределения F(T), определяющая вероятность того, что ресурс будет меньше или равен какому-либо значению t, т.е. F(T)=P(T≤t). Эмпирическая интегральная функция распределения выражает частость (опытную вероятность) события T≤t, а теоретическая интегральная функция распределения - вероятность данного события.
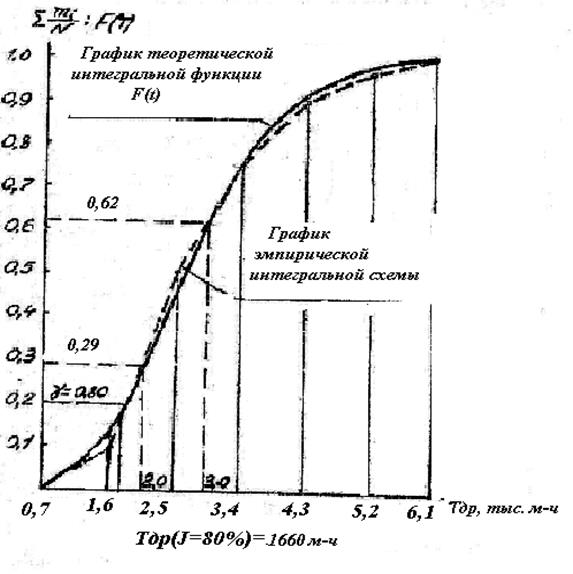
Рисунок 2 - Эмпирическая и теоретическая интегральные функции распределения доремонтного ресурса отверстия под подшипник коробки скоростей станка
Для построения эмпирической интегральной функции распределения ресурса (рис.2) на горизонтальной оси графика откладывают интервальные значения ресурса в тех же границах, а на вертикальной оси – частости, соответствующие границам интервалов (из табл.1). Для рассматриваемого примера значениям ресурса Тдр=0,7 тыс.ч. соответствует частость 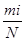 =0 . Поэтому начальная точка строящейся кривой лежит на оси абсцисс и соответствует значению Тдр=0,7 тыс.ч. Значению Тдр=1,6 тыс.ч. соответствует частость
=0 . Поэтому начальная точка строящейся кривой лежит на оси абсцисс и соответствует значению Тдр=0,7 тыс.ч. Значению Тдр=1,6 тыс.ч. соответствует частость 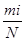 =0,100. Значению Тдр=2,5 (верхняя граница 2-го интервала) соответствует накопленная частость ∑
=0,100. Значению Тдр=2,5 (верхняя граница 2-го интервала) соответствует накопленная частость ∑ 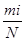 =0,100+0,400=0,500. Так, переходя последовательно от одного интервала к другому, строят график эмпирической функции распределения Тдр. Последняя точка кривой соответствует ∑
=0,100+0,400=0,500. Так, переходя последовательно от одного интервала к другому, строят график эмпирической функции распределения Тдр. Последняя точка кривой соответствует ∑ 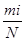 =1,000 для Тдр=6,1 тыс.ч. Построенная по данным табл.1 интегральная кривая накопленных опытных вероятностей представляет собой ломаную линию (рис.2).
=1,000 для Тдр=6,1 тыс.ч. Построенная по данным табл.1 интегральная кривая накопленных опытных вероятностей представляет собой ломаную линию (рис.2).
По пункту 3. На этом этапе статистической обработки опытной информации следует определить числовые характеристики распределения доремонтного ресурса отверстия или сопряжения втулка - палец. Важной числовой характеристикой любой случайной величины является ее среднее значение. На основании средних значений показателей надежности осуществляется решение многих практических задач по планированию работы машин, определению объема ремонтных работ, составлению заявок на запасные части и др.
Следует отметить, что среднее значение случайной величины определяется как среднее арифметическое или среднее взвешенное.
Средняя арифметическая находится как частное от деления суммы отдельных значений случайной величины (Xi) на число слагаемых этой суммы (N):
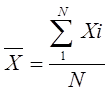 ; (1)
; (1)
Среднее арифметическое значение определяется в тех случаях, когда повторность исходной информации N не велика, и ее не удается объединить в статистический ряд.
При наличии статистического ряда среднее значение случайной величины находится как среднее взвешенное. По заданной студенту опытной информации (N=70 или N=32) среднее значение доремонтного ресурса находится как среднее взвешенное по следующей формуле:
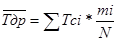 , (2)
, (2)
где Tci-значение ресурса, соответствующее середине i-го интервала.
Для нашего примера
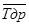 =1,15 ·0,100+2,05 · 0,400+2,95 · 0,260+3,85 · 0,142+4,75 · 0,070+5,65 · 0,028= 2,74 тыс. ч.
=1,15 ·0,100+2,05 · 0,400+2,95 · 0,260+3,85 · 0,142+4,75 · 0,070+5,65 · 0,028= 2,74 тыс. ч.
Другой важной числовой характеристикой распределения ресурса (как случайной величины) является среднее квадратическое отклонение σ, показывающее степень рассеивания отдельных значений ресурса относительно его среднего значения 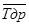 . Его подсчитывают по формуле:
. Его подсчитывают по формуле:
б = 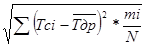 ; (3)
; (3)
Для нашего примера
σ = 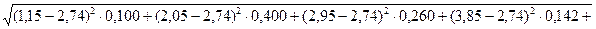
+ (4,75-2,74)2· 0,070+(5,65-2,74)2∙0,028 = 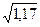 = 1,08 тыс. ч.
= 1,08 тыс. ч.
Значение 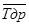 и σ можно определить упрощенным методом суммы (см.|2|с 138…139). Для этого переписывают три первых строки табл. 1 и делают еще две дополнительных строки (табл. 2). Затем в четвертой строке делают один прочерк, в среднем частичном интервале, а в пятой три прочерка: один под прочерком в четвертой строке, а два других – слева и справа от него. В четвертой и пятой строках выполняют последовательное сложение значений по интервалам, соответственно от первого до прочерка и от последнего до прочерка. Полученные суммы складывают влево и вправо от прочерков и получают значения вспомогательных коэффициентов К1,К2 и Л1,Л2 (табл. 2).
и σ можно определить упрощенным методом суммы (см.|2|с 138…139). Для этого переписывают три первых строки табл. 1 и делают еще две дополнительных строки (табл. 2). Затем в четвертой строке делают один прочерк, в среднем частичном интервале, а в пятой три прочерка: один под прочерком в четвертой строке, а два других – слева и справа от него. В четвертой и пятой строках выполняют последовательное сложение значений по интервалам, соответственно от первого до прочерка и от последнего до прочерка. Полученные суммы складывают влево и вправо от прочерков и получают значения вспомогательных коэффициентов К1,К2 и Л1,Л2 (табл. 2).
Используя полученные коэффициенты, подсчитывают два других вспомогательных коэффициента * М1=К1-Л1; М2=К1+Л1+2К2+2Л2.
Таблица 2 – Расчет параметров
| Частичные интервалы Тдр,тыс.м-ч | 0,7… 1,6 | 1,6…2,5 | 2,5… 3,4 | 3,4… 4,3 | 4,3… 5,2 | 5,2… 6,1 | Сумма |
| Середины интервалов Тci,тыс.м-ч | 1,15 | 2,05 | 2,95 | 3,85 | 4,75 | 5,65 | |
| Частоты mi | N=70 | ||||||
| К1=42 | - | Л1=26 | |||||
| К2=7 | - | - | - | Л2=11 |
*Значение коэффициентов могут быть положительными и отрицательными.
Значение среднего доремонтного ресурса 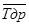 и среднего квадратического отклонения σ подсчитывают по формулам:
и среднего квадратического отклонения σ подсчитывают по формулам:
 = Tci -
= Tci - 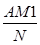 ; (4)
; (4)
σ = А 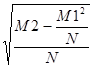 (5)
(5)
где Tci – значение середины того частичного интервала, против которого сделан прочерк в четвертой строке табл.2, тыс. ч (в нашем примере 2,95);
А – значение частичного интервала, тыс. ч (в нашем примере 0,9);
N – общее число значений ресурса (объем информации N=70).
Для нашего примера:
М1 = К1-Л1 = 42-26 = 16
М2 = К1+Л1+2К2+2Л2 = 42+26+2х7+2х11 = 104
Тогда, 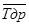 = 2,95 -
= 2,95 - 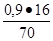 = 2,74 тыс. ч
= 2,74 тыс. ч
σ = 0,9 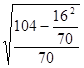 =0,9
=0,9 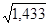 =1,08 тыс.ч
=1,08 тыс.ч
В результате подсчета по методу сумм получены те же значения 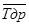 и σ, т.е. 2,74 тыс. ч и 1,08 тыс. ч.
и σ, т.е. 2,74 тыс. ч и 1,08 тыс. ч.
Коэффициент вариации v является безразмерной числовой характеристикой степени рассеивания случайной величины (доремонтного ресурса) и определяется по формуле:
V= 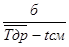 , (6)
, (6)
где tcм – величина смещения начала рассеивания значений Тдр относительно нулевого значения. При объеме информации, которые заданы студенту, величину смещения нужно принимать численно равной нижней границы ряда распределения ресурса. В нашем примере tcм=0,7 тыс. ч.
Тогда,
V= 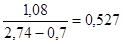
По пункту 4. Опытная информация о значениях случайной величины, заданная студенту, представляет собой некоторую ограниченную выборку из всей генеральной совокупности возможных значений случайной величины (доремонтного ресурса). В связи с этим составленный статистический ряд распределения и эмпирической интегральной функции, а также числовые характеристики распределения имеют ошибки, вызванные исходной информацией. К ошибкам приводит также и некоторый произвол в выборе количества и границ частичных интервалов ряда распределения.
Чтобы ликвидировать влияние ошибок на определение показателя надежности, надо подобрать и использовать теоретический закон распределения (далее ТЗР), характеризующий соотношения между возможными значениями случайной величины (в нашем задании, доремонтного ресурса гильзы или сопряжения) и соответствующими им вероятностями. ТЗР известен, если определены дифференциальная функция f(T) (или функция плотности вероятностей) и теоретическая интегральная функция распределения F(T).
При практических инженерных расчетах показателей надежности часто примерно известен возможный ТЗР, что позволяет выдвинуть гипотезу о нем. А окончательное решение о ТЗР в подтверждение выдвинутой гипотезы принимается с использованием так называемых критериев согласия.
В нашем примере предварительный набор ТЗР ресурса можно сделать по величине коэффициента вариации:
если: V ≤ 0,33 - предлагается нормальный закон распределения (ЗНР)
V >0,33 – выбирается закон распределения Вейбулла (ЗРВ).
В нашем примере при значении V =0,527 целесообразно принять в качестве ТЗР двухпараметрический ЗРВ, для которого:
f(T)= 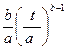
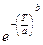 (7)
(7)
F(T)= 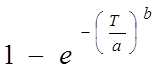 (8)
(8)
т.е. f (T) и F(T) зависят от значений аргумента Т и двух параметров (коэффициентов) «a» и «b». Для этого закона:
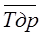 =a ·Kb +tcм; (9)
=a ·Kb +tcм; (9)
σ=а ·Сb; (10)
Коэффициенты a, b, Kb, Cb для ЗРВ находятся по табл. приложения В (или в табл.4 приложения в /2/) в зависимости от значения коэффициента вариации V.
Для нашего примера при V=0,527 находим: b=1,98; Kb=0,886; Cb=0,468
Коэффициент «a» находится из отношения а= σ /Cb=1,08/0,468=2,31
Уточняем средний ресурс: 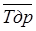 = a ·Kb +tcм = 2,31*0,886+0,7 = 2,74 тыс. ч
= a ·Kb +tcм = 2,31*0,886+0,7 = 2,74 тыс. ч
Значение дифференциальной функции f(T) определяются для середины частичных интервалов Tci, а интегральной функции F(T) – для верхней границы интервалов Tib. Эти значения приведены в зависимости от величины отношений 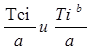 , а также параметра «b» соответственно в табл. Приложений Г и Д. Однако границы частичных интервалов ряда распределения ресурса, принятые в табл.1, следует изменить с поправкой на величину смещения t см.
, а также параметра «b» соответственно в табл. Приложений Г и Д. Однако границы частичных интервалов ряда распределения ресурса, принятые в табл.1, следует изменить с поправкой на величину смещения t см.
Так, если в табл.1 границы первого интервала равны 0,7 и 1,6 тыс. м-ч, то с учетом поправки на величину tcм=0,7 тыс. м-ч они будут 0 и 0,9 тыс. м-ч.
Тогда для первого интервала Tci=0,45 тыс. м-ч, а Tib=0,9 тыс. м-ч.
Расчеты по определению f (T) и F(T) следует представить в виде таблицы 3.
В связи с тем, что расчетные значения «b», 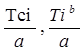 отличаются от табличных, соответствующие значения a ·f (T) и F(T) определяются с использованием двойного интерполирования.
отличаются от табличных, соответствующие значения a ·f (T) и F(T) определяются с использованием двойного интерполирования.
Пример двойного интерполирования для нахождения значения a*f(T).
Для нашего примера: b=1.98 и 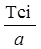 =
= 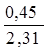 =0,194. Из таблицы Приложения Г находим:
=0,194. Из таблицы Приложения Г находим:
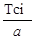 b b | 1.8 | 1.98 | 2.0 |
| 0,1 | 0,280 | 0,198 | |
| 0,194 | Х1 | Х | Х2 |
| 0,2 | 0,470 | 0,384 |
С начала находят значение Х1 и Х2 интерполированием из соотношения:
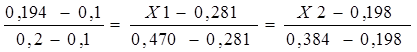 ,
,
Отсюда
Х2 = 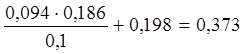
Х1 = 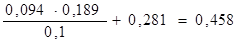
Затем определяют искомое значение a ·f(T)=Х, применяя следующее соотношение:
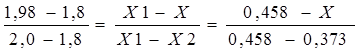 ;
;
тогда Х = 0,458 - 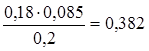
Таким образом, для первого частичного интервала величина a ·f(T)=0,382 и f(T)= 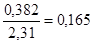 . Результаты заносят в табл. 3. значение F(T) для 1-го интервала из табл. приложения Д, при b=1,98 и
. Результаты заносят в табл. 3. значение F(T) для 1-го интервала из табл. приложения Д, при b=1,98 и 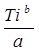 =
= 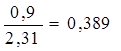 находим, что F(T)=0,140.
находим, что F(T)=0,140.
Аналогично определяет значения f(T) и F(T) для всех частичных интервалов ряда распределения Тдр и заносят в таблицу 3.
Таблица 3 – Уточненные показатели
| Частичные интервалы с учетом tcм=0,7 тыс.м-ч. | 0… 0,9 | 0,9…1,8 | 1,8…2,7 | 2,7…3,6 | 3,6…4,5 | 4,5…5,4 |
| Тсi тыс. м-ч | 0,45 | 1,35 | 2,25 | 3,15 | 4,05 | 4,95 |
| Тci/a | 0,194 | 0,584 | 0,972 | 1,360 | 1,751 | 2,140 |
| a*f(t) | 0,382 | 0,820 | 0,740 | 0,440 | 0,165 | 0,043 |
| f(T) | 0,165 | 0,354 | 0,319 | 0,190 | 0,070 | 0,018 |
| Tib тыс. м-ч. | 0,9 | 1,8 | 2,7 | 3,6 | 4,5 | 5,4 |
| Tib/а | 0,389 | 0,778 | 1,167 | 1,556 | 1,945 | 2,334 |
| F(T) | 0,140 | 0,450 | 0,740 | 0,910 | 0,980 |
По пункту 5. По данным таблицы 3. строят графики функций f (T) и F(T). Дифференциальная функция f(T) строится на рис.1, при этом расчетные ее значения в табл.3 должны соответствовать на графике серединам частичных интервалов без поправки на tсм. Теоретическая интегральная функция F(T) должна располагаться на рис.2 (в координатах эмпирической интегральной функции), причем расчетные ее значения должны соответствовать верхним границам частичных интервалов также без поправки на tсм.
По графику теоретической интегральной функции распределения можно установить 80%-й ресурс отверстия или сопряжения втулка – палец (рис.2). Для этого на оси координат найти величину вероятности отказа, равную 0,2 (т.е. 20%), провести через эту точку горизонтальную линию до пересечения с кривой F(T), а из точки пересечения – вертикальную линию на ось абсцисс. Полученная точка на этой оси определит величину 80%-го ресурса (в нашем примере 1660 м-ч) т.е. к моменту такой наработки 20% отверстий или сопряжений исчерпают свой доремонтный ресурс, а 80% останутся работоспособными и их Тдр превысит величину полученной наработки (напр.1660 ч.).
По графику F(T) определяют также вероятность такого события, что Тдр отверстия или сопряжения втулка –палец будет находится в пределах от 2000 до 3000 м-ч, т.е. Р(2000 ≤ Тдр ≤ 3000). Из рис.2 видно, что вероятность такого события (в нашем примере) Р (Т) = Р (Т=3000) – Р (Т=2000) = 0,62-0,29 = 0,33. Следовательно. около трети отверстий (для нашего примера) будет нуждаться в ремонте после наработки от 2х до 3х тыс. ч.
По пункту 6. Средняя величина доремонтного ресурса является точечной оценкой данного показателя. Она указывает на центр рассеивания (распределения), относительно которого группируется отдельные значения ресурса, приведенные в исходной информации. Для практических расчетов целесообразнее указывать некоторый интервал (т.е. верхнюю и нижнюю границы) значений ресурса, который с некоторой достоверностью включает в себя центр рассеивания ресурса, как случайной величины. Такая оценка Тдр называется интервальной. В практических расчетах принимают величину доверительной вероятности α = 0,80. Для более достоверной (с большей вероятностью) оценки принимают α = 0,90…0,95.
Доверительные границы среднего значения доремонтного ресурса определяют по формулам:
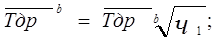
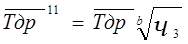 , (11)
, (11)
где b – параметр распределения Вейбулла;
ч1,ч3- коэффициенты, устанавливаемые по табл. приложения Е в зависимости от объема информации N и принятой доверительной вероятности.
Для нашего примера (N=70)
при α1=0,80 находим ч1=1,11; ч3=0,905
Тогда: 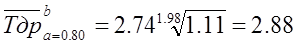 тыс. ч;
тыс. ч;
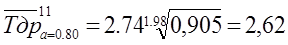 тыс. ч.
тыс. ч.
при α2=0,95 ч1=1,23 и ч3= 0,83
Тогда: 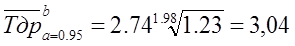 тыс. ч;
тыс. ч;
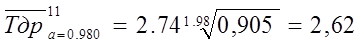 тыс. ч.
тыс. ч.
Таким образом, при повышении достоверности результатов расчета среднего значения случайной величины, границы доверительного интервала расширяются.
Интервальная оценка среднего значения ресурса позволяет определить наибольшую относительную погрешность расчета ±ба. Ее определяют по формулам:
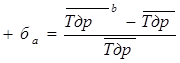 ;
; 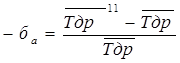 , (12)
, (12)
где, 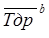 и
и 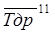 - соответственно верхняя и нижняя границы доверительного интервала среднего значения ресурса.
- соответственно верхняя и нижняя границы доверительного интервала среднего значения ресурса.
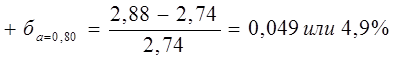
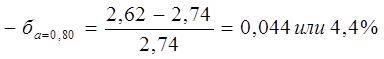
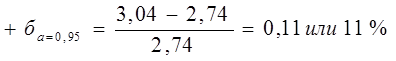
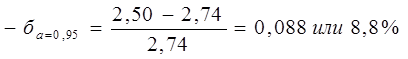
Расчеты показывают, что при оценке среднего значения ресурса с большей достоверностью, получают результаты с меньшей точностью или с большей относительной погрешностью.
Задание 2: Определить полный ресурс сопряжения и допустимые без ремонта размеры сопряженных деталей при следующих исходных данных:
- детали сопряжения – по варианту из таблицы Приложения И.
- средняя межремонтная наработка Тмр=2000 час.
