Критерии работоспособности и устойчивости
Работа замкнутой системы управления второго порядка основана на критериях:
· обеспечение хорошей динамики;
· небольшая или нулевая статическая ошибка;
· малое время переходных процессов.
Предполагаем, что возмущения отсутствуют. Тогда из уравнения (17-7) видно, что мы имеем систему второго порядка с нулевым корнем. Характеристическое уравнение системы второго порядка может быть записано в стандартной форме:
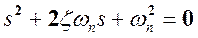 , (17-8)
, (17-8)
где 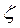 и
и 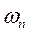 - соответственно коэффициент демпфирования и собственная частота колебаний системы;
- соответственно коэффициент демпфирования и собственная частота колебаний системы;
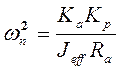 (17-9)
(17-9)
и 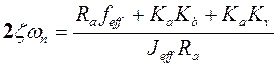 . (17-10)
. (17-10)
Работа системы второго порядка определяется значениями ее собственной частоты колебаний 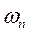 и коэффициентом демпфирования
и коэффициентом демпфирования 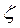 . Для устранения колебаний и резонанса конструкции сочленения необходимо выбирать значение частоты собственных колебаний, не превышающих половины величины резонансной частоты конструкции сочленения:
. Для устранения колебаний и резонанса конструкции сочленения необходимо выбирать значение частоты собственных колебаний, не превышающих половины величины резонансной частоты конструкции сочленения: 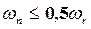 , где
, где 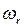 - резонансная частота конструкции сочленения, (рад/с). Резонансная частота конструкции зависит от материала, из которого изготовлен манипулятор. Если эффективную жесткость сочленения обозначить
- резонансная частота конструкции сочленения, (рад/с). Резонансная частота конструкции зависит от материала, из которого изготовлен манипулятор. Если эффективную жесткость сочленения обозначить 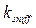 , то возвращающий момент
, то возвращающий момент 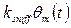 противодействует моменту инерции двигателя:
противодействует моменту инерции двигателя:
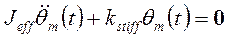 . (17-11)
. (17-11)
Произведя преобразование Лапласа, получим характеристическое уравнение выражения (17-11) в виде:
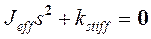 . (17-12)
. (17-12)
Решение этого уравнения дает резонансную частоту конструкции системы:
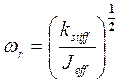 . (17-13)
. (17-13)
Для того, чтобы скомпенсировать силы тяжести и центробежные силы, можно вычислить величины моментов от них и эти значения подать в устройство управления, как это показано на рис. 17.3, с целью минимизации их влияния. Такая компенсация называется компенсацией по прямой связи.
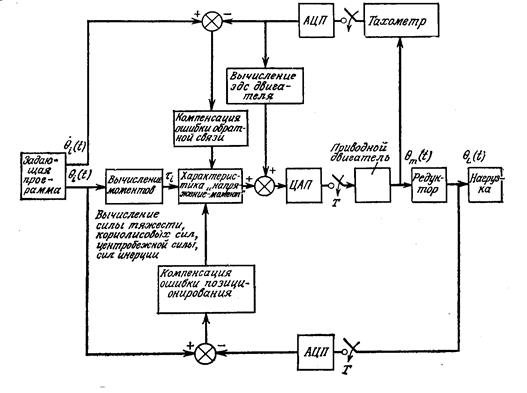
Рисунок 17.3. Компенсация возмущений
Если момент компенсации 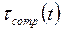 создается только силой тяжести звена манипулятора, выражение для статической ошибки позиционирования:
создается только силой тяжести звена манипулятора, выражение для статической ошибки позиционирования:
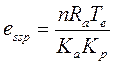 , (17-14)
, (17-14)
где 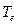 - момент, выраженный через преобразование Лапласа.
- момент, выраженный через преобразование Лапласа.
В общем случае уравнения Лагранжа-Эйлера, описывающие движение манипулятора с шестью сочленениями без учета динамики электронного управляющего блока, трения в редукторе и люфтов, могут быть записаны в виде, соответствующем уравнению (10-11):
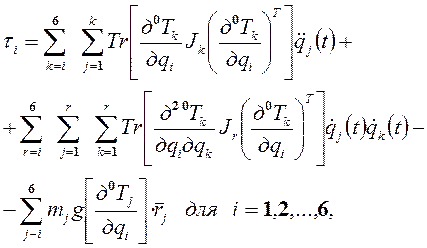 (17-15)
(17-15)
где 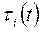 - обобщенный управляющий момент в i-м сочленении для перемещения i-го звена;
- обобщенный управляющий момент в i-м сочленении для перемещения i-го звена; 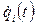 и
и 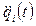 - соответственно угловая скорость и угловое ускорение i-го сочленения;
- соответственно угловая скорость и угловое ускорение i-го сочленения; 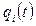 - обобщенная координата манипулятора, определяющая его угловое положение;
- обобщенная координата манипулятора, определяющая его угловое положение; 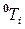 - однородная матрица преобразования для звена размерностью 4×4, которая связывает пространственное расположение между двумя системами координат (i-й и базовой);
- однородная матрица преобразования для звена размерностью 4×4, которая связывает пространственное расположение между двумя системами координат (i-й и базовой); 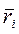 - положение центра масс i-го звена относительно i-й координаты системы;
- положение центра масс i-го звена относительно i-й координаты системы; 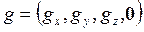 - линейный вектор силы тяжести,
- линейный вектор силы тяжести, 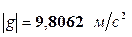 ;
; 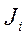 - матрица псевдоинерции i-го звена относительно системы координат i-го звена, которая может быть записана в соответствии с уравнением (10-5).
- матрица псевдоинерции i-го звена относительно системы координат i-го звена, которая может быть записана в соответствии с уравнением (10-5).
Эта компенсация соответствует тому, что обычно называют методом обратной задачи динамики или методом вычисления момента.
Лекция 18
