Метод итераций (повторений)
Пусть М – некоторое множество (значения должны быть допустимы ), Р подмножество М, где Р – множество решений. При этом х Î Р Û p(х)=истина. Пусть Т некоторое преобразование из М\Р в М, т.е. Т:М\Р®М.
Метод итераций (дословно – повторений) состоит в том, что строится некоторое преобразование (отображение) Т:М\Р®М и это преобразование последовательно применяется, начиная с какого-то х0ÎM:
X1=T(x0), x2=T(x1), …, xn=T(xn-1), …
до тех пор, пока мы впервые не получим xi такое, что p(xi)=истина (естественно, должна быть уверенность, что рано или поздно такое xi найдется).
Напишем программу, находящую х. Пусть х0ÎМ (некоторая точка М) – начальное значение.
x :=х0; {хÎМ}
while not p(x) do
begin
{xÎM\P}
x :=T(x);
{xÎM}
end;
{xÎP}
Для корректности данной программы необходимо и достаточно доказать, что цикл завершится за конечное число шагов.
Иллюстрация работы программы:
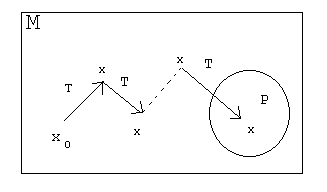
При этом множества М и Р могут быть выбраны различными способами.
Примеры:
 |
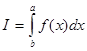1. Вычисление интеграла Римана
Для вычисления интеграла необходимо разбить отрезок [a,b] на р частей. При этом Ip » I, где Ip – квадратурная форма. Если увеличить количество разбиений в к раз, то получим Ipk » I. При этом если подынтегральная функция достаточно гладкая, то I - Ikp = ( Ikp - Ip )/(ks+1-1)+o(p-s), где s – степень точности формулы. Данная формула оценки погрешности через старший член лежит в основе метода Рунге.
При этом величина Ikp + (Ikp - Ip)/(ks+1 - 1) будет точнее, чем Ikp. Она носит название первого шага метода Ромберга.
Рассмотрим программу вычисления интеграла.
{$N+}
Type _Real = single;
fr2r = function (x: _Real):_Real;
Function Integral (a, b: _Real; f: fr2r; eps: Real):Real;
{a, b – пределы интегрирования, f – достаточно гладкая подынтегральная функция; eps>0 – критерий Рунге. Функция возвращает приближенное значение интеграла Римана}
var
Iprev, Ipost, R: _Real;
p: word;
h: _Real;
const p0=16;
k=2;{или 3}
gamma=…..{ks+1-1};
{далее могут следовать другие необходимые константы}
begin
if a=b then begin Integral:=0.0; exit; end;
p:=p0;
h:=(b-a)/p;
{Вычисление Ipost для числа разбиений p, а также, возможно, его частей}
R:=1e30;
While abs (R) > eps do
Begin
Iprev := Ipost;
P := p*k;
h := h/k;{p-иногда не обязателен}
{Вычисляем Ipost для p разбиений, и, возможно, его части}
R := (Ipost- Iprev)/gamma;
End;
Integral := Ipost+R;
End;
Замечания:
1) Процесс сопровождают погрешности округления. Поэтому если eps выбрать достаточно малой, то процесс зациклится.
2) Вычисление квадратурных сумм следует организовать так, чтобы погрешность была меньше. Для этого, например, суммы необходимо накапливать с более высокой точностью.
2. Вычисление функции Бесселя J0(x) = å (-1)k((x/2)2k/(k!)2), где k изменяется от 0 до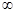 
. С другой стороны J0(x)» 
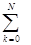(-1)k((x/2)2k/(k!)2).
Данный ряд сходится к функции Бесселя при любом значении аргумента.
Суммирование производится до тех пор, пока элемент ряда не станет меньше значения погрешности, т.е. êaNú <eps.
Напишем простейшую программу подсчитывающую значение функции Бесселя по ряду.
Function J0 (x, eps : _Real):_Real;
{x – аргумент функции, eps>0 – погрешность округления. Функция возвращает приближенное значение функции Бесселя}
var
k : word;
a, s : _Real;
begin
k := 0;
a :=1.0;
s := 1.0;
while abs(a) > eps do
begin
k := k + 1;
a := -a * sqr (x/2.0) / sqr (k);
s:=s+a;
end;
j0 := s;
end;
При этом k лучше было бы хранить как вещественное число.
Для увеличения скорости работы программы удобно затабулировать квадрат знаменателя. Запишем разность знаменателей на следующих один за другим шагах цикла. Zk+1 = (k+1)2-k2 = 2k + 1, в свою очередь, табулируя полученную линейную функцию, получаем Uk+1 = Zk+1 –Zk = 2. Таким образом нахождение k2 сводится к сложению представленному следующей таблицей:
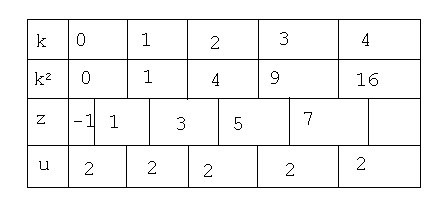
Теперь мы можем написать подпрограмму, которая будет несравненно лучше предыдущей.
Type _Real = single;
Function J0 (x, eps : _Real) : _Real;
{x – значение аргумента, eps>0 – погрешность округления. Функция возвращает приближенное значение функции Бесселя}
const u : _Real = 2.0;
var
s, a, z, z0, r : _Real;
begin
a := 1.0;
s := a;
z := -1.0;
z0 := 0.0;
r := -sqr (x/2.0);
while abs (a) > eps do
begin
z := z + u;
z0 := z0 + z;
a := a*r/z0;
s:=s+a;
end;
J0 := s;
end;
Математические свойства данной программы будут те же, т.к. используется тот же математический аппарат.
Функция Бесселя, вычисляемая в данной программе характеризуется следующими графиками :
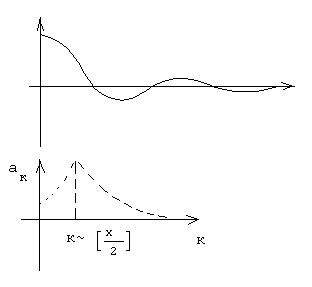
maxçakú ~ ((x/2)2[x/2]/([x/2]!)2)
maxçDakú ~ b1-t maxçakú, где t – длина мантиссы, b - основание системы счисления принятой в компьютере.
Таким образом, не следует брать слишком маленькие значения eps. Минимальное значение eps зависит от х и возрастает с ростом модуля х.
Из всего вышесказанного можно сделать вывод, что метод рядов Тейлора хотя и является хорошим математическим аппаратом для исследований, но не приспособлен для вычислений, т.к. область его применения ограничивается небольшой окрестностью точки разложения (в данном случае точки 0).
Метод инварианта цикла.
Метод инварианта цикла является частным случаем метода итераций.
Задается некоторое множество величин М, РÌ М – подмножество результатов. Надо найти точку х Î Р. Для этого выделим множества IÌ M и QÌ M причем такие, что Æ ¹ I Ç Q Ì P. Таким образом, наша задача сводится к нахождению точки, которая будет принадлежать пересечению этих множеств. Причем использовать будем только такие преобразования, которые не выходят из I, то есть в нашем случае принадлежность точки множеству I является инвариантом (величиной неизменной).
Пусть x0 Î I – начальная точка.
Т:I\Q®I – преобразование инвариантно относительно принадлежности точки множеству I.
Иллюстрация к вышесказанному:
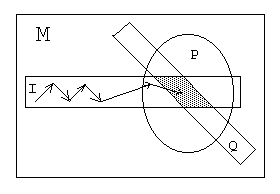
Под действием преобразования Т точка х0 переходит в некоторую точку х1, принадлежащую множеству I. Точка х1, в свою очередь, переходит в точку х2, также принадлежащую I. Этот процесс продолжается пока некоторая точка хN не перейдет в точку принадлежащую некоторому множеству Q, которое выбрано так чтобы его пересечение с I содержалось в P. Полученная точка с одной стороны принадлежит Q, а с другой принадлежит I, в силу инвариантности преобразования Т относительно I.
Схема программы:
x := x0; {xÎI}
while not q(x) do
begin
{x ÎI\Q}
x := T(x);
{x Î I}
end;
{x Î IÇQ Ì P}
Напишем программу иллюстрирующую вышеописанный метод, которая будет обеспечивать возведенее числа в целую положительную степень.
Type _Real = single;
_Unsign = word;
function power (x : _Real; n: _Unsign ):Real;
{х - основание, n – показатель. Подпрограмма обеспечивает возведение в степень }
var z := _Real;
begin
z := 1.0;
while n > 0 do {z*xn - инвариант}
begin
if odd(n) then {проверка нечетности}
begin
dec(n); {n:=n-1}
z := z*x;
end
else begin
n := n chr 1; {n := n div 2}
x := sqr(x);
end;
end;
power := z;
end;
Докажем, что данная программа завершится за конечное число шагов. Подпрограмма завершает свою работу когда z = xn, т.е. пердназначена для возведения х в n – ую степень. Число повторений равно количество “0” + 2*количество “1” –1 в двоичной записи числа n <= 2*количество значащих цифр – 1 в двоичной записи = 2*]log2n[ - 1. При этом данная программа будет очень эффективна.
Метод инвариантной функции.
Метод инвариантной функции является частным случаем метода инварианта цикла.
В данном случае х = х0 и необходимо вычислить f(x0). При этом
I = {множество x | f(x) = f(x0)}
P = {множество x | f(x) вычисляется легко}.
Построим преобразование Т – инвариантное относительно I, а в качестве условия окончания примем само значение P (Q = P).
Схема программы:
x := x0; {x Î I}
while not p(x) do
begin {x Î I\P}
x := T(x); {x Î I}
end; {x Î P Ç I}
result := f(x);
Для доказательства правильности достаточно доказать, что цикл выполнится за конечное число шагов.
Напишем программу иллюстрирующую данный метод.
Пусть x = (a, b), а f(x) = Н.О.Д.(a, b). Необходимо вычислить Н.О.Д.(a, b).
В данной программе будет использоваться тот факт, что делитель двух чисел
будет являться делителем их разности.
a := a0; b := b0; {>=0}
while (a>0) and (b>0) do
begin
if a>b then a := a - b
else b := b – a;
end;
result := a+b; { условием выхода из цикла является равенство 0 либо a, либо b, поэтому сумма этих чисел будет нам давать то из чисел которое не равно 0 }