Матричные игры (продолжение - 2)
ПРИБЛИЖЕННЫЙ МЕТОД РЕШЕНИЯ МАТРИЧНЫХ ИГР Иногда можно ограничиться приближенным решением матричной игры. В основе приближенного метода лежит предположение, что игроки выбирают свои стратегии в очередной партии, руководствуясь накапливающимся опытом уже сыгранных партий..
| ПРИМЕРЫ 6.Найдем приближенное решение матричной игры, смоделировав 10 партий  Игрок А начинает со своей 1-й стратегии. Соответствующие выигрыши (1-я строка матрицы) запишем в столбцы В1, В2, В3 и определим среди них минимальный (выделен в строке 1). Он соответствует стратегии В1 игрока В. Поэтому его соответствующие выигрыши (первый столбец матрицы) запишем в столбцы А1, А2, А3 и определим среди них максимальный (выделен в строке 1). Он соответствует стратегии А2. Поэтому во второй партии игрок А ответит стратегией А2. Соответствующие выигрыши (2-я строка) надо прибавить к числам в столбцах В1, В2, В3 предыдущей строки и определить среди них минимальный (выделен в строке 2), что соответствует стратегии В3 игрока В. Поэтому его соответствующие выигрыши (3-й столбец) надо прибавить к числам в столбцах А1, А2, А3 предыдущей строки игрока В и определить среди них максимальный, что соответствует стратегии А2 игрока А. И т.д. Приближенное значение нижней цены игры в каждой партии: α=(выделенное число в столбцах В1, В2, В3)/(номер партии) Приближенное значение верхней цены игры в каждой партии: β=(выделенное число в столбцах А1, А2, А3)/(номер партии) После десяти партий v≈7,8. Поэтому для исходной матрицы v≈7,8/10=0,78. pi ≈(число использования стратегии Аi)/(число партий) qj ≈(число использования стратегии)/(число партий) Число использования стратегииАi =число отмеченных элементов в столбце Аi Число использования стратегииBj =число отмеченных элементов в столбце Bj После десяти партий: p1=3/10, p2=6/10, p3=1/10 (за десять партий игрок А три раза воспользовался стратегией А1, шесть раз – стратегией А2, и один раз стратегией А3). q1=1/10, q2=4/10, q3=5/10 (за десять партий игрок B один раз воспользовался стратегией В1, четыре раза – стратегией В2, и пять раз стратегией В3). Игрок А начинает со своей 1-й стратегии. Соответствующие выигрыши (1-я строка матрицы) запишем в столбцы В1, В2, В3 и определим среди них минимальный (выделен в строке 1). Он соответствует стратегии В1 игрока В. Поэтому его соответствующие выигрыши (первый столбец матрицы) запишем в столбцы А1, А2, А3 и определим среди них максимальный (выделен в строке 1). Он соответствует стратегии А2. Поэтому во второй партии игрок А ответит стратегией А2. Соответствующие выигрыши (2-я строка) надо прибавить к числам в столбцах В1, В2, В3 предыдущей строки и определить среди них минимальный (выделен в строке 2), что соответствует стратегии В3 игрока В. Поэтому его соответствующие выигрыши (3-й столбец) надо прибавить к числам в столбцах А1, А2, А3 предыдущей строки игрока В и определить среди них максимальный, что соответствует стратегии А2 игрока А. И т.д. Приближенное значение нижней цены игры в каждой партии: α=(выделенное число в столбцах В1, В2, В3)/(номер партии) Приближенное значение верхней цены игры в каждой партии: β=(выделенное число в столбцах А1, А2, А3)/(номер партии) После десяти партий v≈7,8. Поэтому для исходной матрицы v≈7,8/10=0,78. pi ≈(число использования стратегии Аi)/(число партий) qj ≈(число использования стратегии)/(число партий) Число использования стратегииАi =число отмеченных элементов в столбце Аi Число использования стратегииBj =число отмеченных элементов в столбце Bj После десяти партий: p1=3/10, p2=6/10, p3=1/10 (за десять партий игрок А три раза воспользовался стратегией А1, шесть раз – стратегией А2, и один раз стратегией А3). q1=1/10, q2=4/10, q3=5/10 (за десять партий игрок B один раз воспользовался стратегией В1, четыре раза – стратегией В2, и пять раз стратегией В3). |
БИМАТРИЧНЫЕ ИГРЫ
БИМАТРИЧНАЯ ИГРА 2×2: ОПРЕДЕЛЕНИЕ И ВОЗМОЖНЫЕ СТРАТЕГИИ ИГРОКОВ
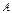 и и 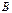 не являются противоположными не являются противоположными  . В этом случае у каждого игрока будет своя платежная матрица. Такие игры называют биматричными. Ограничимся рассмотрением биматричных игр 2×2, когда у каждого игрока всего по две стратегии: . В этом случае у каждого игрока будет своя платежная матрица. Такие игры называют биматричными. Ограничимся рассмотрением биматричных игр 2×2, когда у каждого игрока всего по две стратегии:  и и  соответственно. Матрицы игры в этом случае – квадратные матрицы 2-го порядка соответственно. Матрицы игры в этом случае – квадратные матрицы 2-го порядка СРЕДНИЕ ВЫИГРЫШИ ИГРОКОВ. РАВНОВЕСНАЯ СИТУАЦИЯ
 вероятности вероятности  и и  , а стратегиям , а стратегиям  вероятности вероятности  и и  соответственно. соответственно. Средний выигрыш игрока Средний выигрыш игрока Пара чисел
То есть отклонение от оптимальной стратегии одного из игроков при условии, что другой придерживается своей оптимальной стратегии, уменьшает средний выигрыш отклонившегося игрока. ТЕОРЕМА НЕША Любая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях. НАХОЖДЕНИЕ РАВНОВЕСНЫХ СИТУАЦИЙ Введем обозначения: Пусть игрок решение которой дает Аналогично, если игрок
Изобразим обе полученные линии в координатах | ПРИМЕР 7.Решение и графическая иллюстрация  биматричной игры биматричной игры
Совместим оба графика. Получилась одна точка пересечения
Средний выигрыш игрока
Средний выигрыш игрока
|
ПОЗИЦИОННЫЕ ИГРЫ
| ПОЗИЦИОННЫЕ ИГРЫ: ОСНОВНЫЕ ПОНЯТИЯ Позиционные игры – бескоалиционные игры, моделирующие процессы последовательного принятия решений игроками в условиях меняющейся по времени и, вообще говоря, неполной информации. Позиции – это состояния игры, альтернативы – это возможный выбор в каждой позиции. Для наглядности в позиционных играх используют схему "дерево решений". В позиционных играх с полной информацией игрок перед своим ходом знает ту позицию дерева игры, в которой он находится. В позиционных играх с нгеполной информацией игрок перед своим ходом не знает точно ту позицию дерева игры, в которой он фактически находится. Нормализация позиционной игры – это процесс сведения позиционной игры к матричной или биматричной играм. | ПРИМЕР 8.Нормализация и решение позиционной игры  Фирма Фирма 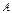 контролирует рынок некоторого товара. Фирма контролирует рынок некоторого товара. Фирма 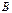 решает, стоит ли выходить на рынок этого товара. Стратегии фирмы решает, стоит ли выходить на рынок этого товара. Стратегии фирмы  : выходить ( : выходить (  ), не выходить ( ), не выходить (  ). В свою очередь фирма ). В свою очередь фирма  решает, стоит ли снижать объем производства этого товара. Стратегии фирмы решает, стоит ли снижать объем производства этого товара. Стратегии фирмы  : сохранить объем производства ( : сохранить объем производства (  ), сократить объем производства ( ), сократить объем производства (  ). Изобразим дерево игры и выигрыши игроков. ). Изобразим дерево игры и выигрыши игроков.   Матрицы биматричной игры запишутся в виде: Матрицы биматричной игры запишутся в виде:
а) решение которой дает
Совместим оба графика. Получилась три точки пересечения, то есть три равновесных ситуации: 1) Средний выигрыш игрока Средний выигрыш игрока 2) Средний выигрыш игрока Средний выигрыш игрока 2) Средний выигрыш игрока Средний выигрыш игрока |
| ПОЗИЦИОННЫЕ ИГРЫ: ОСНОВНЫЕ ПОНЯТИЯ Позиционные игры – бескоалиционные игры, моделирующие процессы последовательного принятия решений игроками в условиях меняющейся по времени и, вообще говоря, неполной информации. Позиции – это состояния игры, альтернативы – это возможный выбор в каждой позиции. Для наглядности в позиционных играх используют схему "дерево решений". В позиционных играх с полной информацией игрок перед своим ходом знает ту позицию дерева игры, в которой он находится. В позиционных играх с нгеполной информацией игрок перед своим ходом не знает точно ту позицию дерева игры, в которой он фактически находится. Нормализация позиционной игры – это процесс сведения позиционной игры к матричной или биматричной играм. | ПРИМЕР 8.Нормализация и решение позиционной игры  Фирма Фирма  контролирует рынок некоторого товара. Фирма контролирует рынок некоторого товара. Фирма 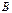 решает, стоит ли выходить на рынок этого товара. Стратегии фирмы решает, стоит ли выходить на рынок этого товара. Стратегии фирмы 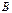 : выходить ( : выходить (  ), не выходить ( ), не выходить (  ). В свою очередь фирма ). В свою очередь фирма 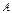 решает, стоит ли снижать объем производства этого товара. Стратегии фирмы решает, стоит ли снижать объем производства этого товара. Стратегии фирмы 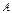 : сохранить объем производства ( : сохранить объем производства (  ), сократить объем производства ( ), сократить объем производства (  ). Изобразим дерево игры и выигрыши игроков. ). Изобразим дерево игры и выигрыши игроков.   Матрицы биматричной игры запишутся в виде: Матрицы биматричной игры запишутся в виде:
а) решение которой дает
Совместим оба графика. Получилась три точки пересечения, то есть три равновесных ситуации: 1) Средний выигрыш игрока Средний выигрыш игрока 2) Средний выигрыш игрока Средний выигрыш игрока 2) Средний выигрыш игрока Средний выигрыш игрока Наши рекомендации
|






 .
.
 определяет равновесную ситуацию, если
определяет равновесную ситуацию, если для всех
для всех  .
. с учетом которых средние выигрыши игроков запишутся в виде:
с учетом которых средние выигрыши игроков запишутся в виде:  .
. . Запишем условие равновесия для среднего выигрыша игрока
. Запишем условие равновесия для среднего выигрыша игрока  . Откуда получаем систему
. Откуда получаем систему  ,
,


 . Точки пересечения этих линий, лежащие в квадрате
. Точки пересечения этих линий, лежащие в квадрате  и
и  .
.
 а)
а)  . Получим систему:
. Получим систему:  , решение которой дает
, решение которой дает
 б)
б)  . Получим систему:
. Получим систему:  , решение которой дает
, решение которой дает

 , то есть одна равновесная ситуация
, то есть одна равновесная ситуация  .
.




 . Получим систему:
. Получим систему:  ,
,
 б)
б)  . Получим систему:
. Получим систему:  ,
, решение которой дает
решение которой дает 
 ,
,  (фирма
(фирма 

 ,
,  (фирма
(фирма 

 ,
, 
