Задания для контрольной работы № 1
1.1-4. Передача экономической информации от пункта A в пункт В может осуществляться по следующей схеме:
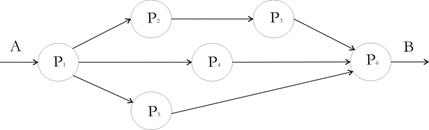
Здесь Pi – вероятности передачи информации без искаженнй i-ом блоке. Определить надежность данной схемы, т.е. Вероятность получения в пункте В достоверной (без искажений) информации.
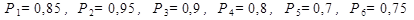
Решение:
А — событие, когда получена достоверная информация. Согласно формулам сложения и умножения вероятностей получаем:
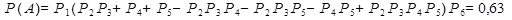 .
.
Ответ: 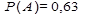
1.2-4. На 3 станках при одинаковых и независимых условиях изготавливаются детали одного наименования. На первом станке изготавливается а%, на втором - b%, на третьем - с% всех деталей. Для каждой детали вероятность быть бездефектной равна p1, если она изготовлена на первом станке, p2 - если она изготовлена на втором станке, p3 - если она изготовлена на третьем станке. Найти вероятность того, что наугад взятая деталь не окажется дефектной.
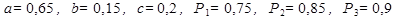
Решение:
А — событие, когда взятая деталь недефектная, тогда согласно формуле сложения веротностей получаем: 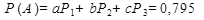 .
.
Ответ: 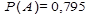
1.3-4. На склад поступила партия N деталей, среди которых М дефектных. Из партии для контроля выбираются случайным образом К деталей. Если среди контрольных окажется более L дефектных, то вся партия бракуется. Найти вероятность того, что партия будет забракована.
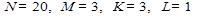
Решение:
А — событие, когда партия забракована. 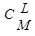 - возможность выбрать L деталей из M дефектных,
- возможность выбрать L деталей из M дефектных, 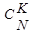 - возможность выбрать K изделий из общего количества N,
- возможность выбрать K изделий из общего количества N, 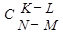 - возможность выбрать детали из недефектных, тогда
- возможность выбрать детали из недефектных, тогда 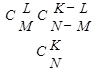 - вероятность выбрать ровно L бракованных деталей. Тогда
- вероятность выбрать ровно L бракованных деталей. Тогда

Ответ: 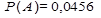
4.12.В одном ящике упаковано N1 деталей, из них M1 с дефектами; в другом ящике упаковано N2 деталей, из них M2 с дефектами. Контролер случайным образом открыл один из этих ящиков и взял деталь на экспертизу. Деталь оказалась с дефектом. Какова вероятность того, что и вторая деталь из того же ящика окажется с дефектом?
N1=20 N2=22
M1=3 M2=2
Решение:
пусть В – это событие, соответствующее тому, что первая взятая из ящика деталь является бракованной. Тогда по формуле полной вероятности можно найти вероятность этого события:
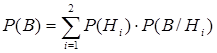 , где
, где
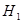 - контролер взял деталь из первого ящика,
- контролер взял деталь из первого ящика,
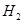 - контролер взял деталь из второго ящика.
- контролер взял деталь из второго ящика.
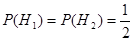
Для вычисления вероятностей гипотез при условии события В, воспользуемся формулой 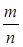 :
: 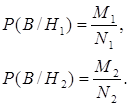
Отсюда видно, что вероятность события В равна:
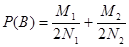 .
.
Для решения исходной задачи будем пользоваться также формулой полной вероятности, но примененной к новым гипотезам:
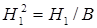 - наугад взятая из первого ящика деталь оказалась бракованной.
- наугад взятая из первого ящика деталь оказалась бракованной.
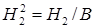 - наугад взятая из второго ящика деталь оказалась бракованной.
- наугад взятая из второго ящика деталь оказалась бракованной.
По формуле Байеса найдем вероятности новых гипотез:
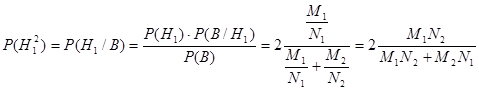
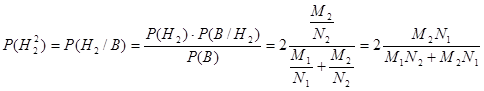
Пусть А – это событие, соответствующее тому, что вторая взятая из того же ящика, что и первая деталь, окажется бракованной. Тогда:
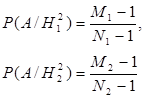
В итоге, для нахождения вероятности события А вновь воспользуемся формулой вероятности: