Имитационное моделирование. Проведем имитацию исполнения контракта при оптимальных значениях стимулирующих
Проведем имитацию исполнения контракта при оптимальных значениях стимулирующих выплат.
Поскольку результаты деятельности фирмы в модели получены при допущении, что доход есть случайная величина, распределение которой зависит от усилий агента, необходимо имитировать её многократную реализацию. Каждая реализация соответствует малому периоду времени, по истечению которого происходит подведение итогов, с определением заработной платы агента и определением прибыли фирмы.
Исходные данные
Выбор величины дохода 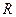 будем осуществлять с помощью генератора случайных чисел, который генерирует значение случайной величины, имеющей следующее распределение:
будем осуществлять с помощью генератора случайных чисел, который генерирует значение случайной величины, имеющей следующее распределение:
| xi | ||
| pi | 1/3 | 2/3 |
Чтобы обеспечить реализацию этой случайной величины в MS Excel используем функцию СЛЧИС(), которая вычисляет значения равномерно распределенной случайной величины в интервале [0;1]. Пусть число  является значением функции СЛЧИС(),тогда величина
является значением функции СЛЧИС(),тогда величина 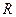 , вычисленная по правилу
, вычисленная по правилу

будет иметь искомое распределение.
Решение приведено на рис. 11-16. На рис. 11. приведены расчеты по аналитическим формулам, (ЧЧ).

Рис. 11. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Имитационное моделирование исполнения контракта при оптимальных значениях стимулирующих выплат (начало).

Рис. 12. Фрагмент электронных таблиц MS Excel в режиме отображения формул. Имитационное моделирование исполнения контракта при оптимальных значениях стимулирующих выплат (начало).
Сам процесс имитации реализован в строках ниже 34. Подведение итогов имитации приведено в строках 19-33. Такое расположение итогов (выше самой имитации) позволяет при необходимости увеличить количество имитируемых периодов, вставив необходимое количество строк или дописав их в конец, без сильного изменения итогов.
При имитации каждому периоду времени соответствует одна строчка таблицы. Всего промоделировано 500 временных периодов. В интервалах N34:N534 и O34:O534 содержатся реализации искомых случайных величин  (равномерно распределенная случайная величина) и
(равномерно распределенная случайная величина) и 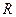 (доход фирмы) соответственно. В столбцах P,Q и R содержатся вычисленные значения заработной платы работника, прибыль фирмы и полезности агента.
(доход фирмы) соответственно. В столбцах P,Q и R содержатся вычисленные значения заработной платы работника, прибыль фирмы и полезности агента.

Рис. 13. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Имитационное моделирование, многократного повторения производственного периода (продолжение).

Рис. 14. Фрагмент электронных таблиц MS Excel в режиме отображения формул. Имитационное моделирование, многократного повторения производственного периода (продолжение).
Подведение итогов моделирования и сравнение с расчетными результатами приведено на рис.15.-16. Анализ показал, что количество неудачных и удачных периодов при 500 повторениях производственного цикла равно 162 и 338 соответственно, а доли в общем количестве повторений равны 0,324 и 0,676 соответственно. Доли незначительно отличаются от теоретических(вероятностей) , отклонения равны 2.80% и 1.4% соответственно. Это показывает что при таком количестве повторений реализация случайной величины – дохода фирмы проведена корректно.
Средние значения дохода фирмы, заработной платы работника, прибыли фирмы и полезности работника по результатам имитации находятся в интервале ячеек О27:R27 соответственно.
Сравнение этих средних значений с вычисленными значениями по основным формулам проведено в интервале ячеек О30:R30. Очевидно, что они несущественно отличаются, так отклонения лежат в диапазоне от 0,80% для величины дохода фирмы до 2,80% для полезности работника. Наличие отклонений обусловлено случайностью величины дохода фирмы. Более точные значения можно, как правило, получить, увеличив количество имитаций.

Рис.15. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Подведение итогов имитационного моделирования и сравнение с расчетными результатами (окончание).

Рис. 16. Фрагмент электронных таблиц MS Excel в режиме отображения формул. Подведение итогов имитационного моделирования и сравнение с расчетными результатами (окончание).
Проведем имитацию исполнения контракта при отсутствии стимулирующих выплат.
Процесс имитации аналогичен случаю, рассмотренному выше за исключением того, что выплаты работнику не являются случайной величиной, а являются константой равной 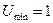 . В условиях не симметричности информации работник ожидаемо работает с низким уровнем усилий
. В условиях не симметричности информации работник ожидаемо работает с низким уровнем усилий 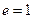 . Результаты расчетов приведены на рис. 17-18.
. Результаты расчетов приведены на рис. 17-18.

Рис. 17. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Имитационное моделирование исполнения контракта при отсутствии стимулирующих выплат (начало).

Рис. 18. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Подведение итогов имитационного моделирования исполнения контракта при отсутствии стимулирующих выплат и сравнение с расчетными результатами (окончание)
Анализ показал, что количество неудачных и удачных периодов при 500 повторениях производственного цикла равно 337 и 167 соответственно, а доли в общем количестве повторений равны 0,666 и 0,334 соответственно. Доли незначительно отличаются от теоретических (вероятностей), отклонения равны 0.10% и 0.2% соответственно. Это показывает что при таком количестве повторений реализация случайной величины – дохода фирмы проведена корректно.
Средние значения дохода фирмы, заработной платы работника, прибыли фирмы и полезности работника по результатам имитации находятся в интервале ячеек C27:F27 соответственно.
Сравнение этих средних значений с вычисленными значениями по основным формулам проведено в интервале ячеек C30:F30. Очевидно, что заработная плата и полезности работника являются постоянными величинами и полностью совпадают с расчетными значениями. Величины дохода и прибыли фирмы отличаются на 0,08% и 0,09% соответственно, что можно расценить как несущественное отклонение. Наличие отклонений обусловлено случайностью величины дохода фирмы, ещё более точные значения можно, как правило, получить, увеличив количество имитаций.
Выводы.
- Сравнивая прибыль фирмы (ячейка F16) равную 15.667 в случае отсутствия стимулирующих выплат с прибылью фирмы с прибылью в случае наличия стимулирующих выплат (ячейка R16) равной 17.667, приходим к выводу, что фирме в случае несимметричности информации, выгоднее заключать стимулирующий контракт.
- Вспомним, что в самой выгодной для фирмы ситуации, когда работник прилагает усилия высокого уровня, а получает постоянную низкую зарплату, прибыль фирмы была равна 19.333. Уменьшение прибыли (в случае стимулирующего контракта) произошло потому, что, выплачивая работнику более высокую заработную плату, фирма делится прибылью с работником, а работник получает дополнительную плату за риск. Риск состоит в том, что его зарплата зависит не только от его усилий, но и других факторов.
Задание на 3 балла
Определить наилучший контракт с точки зрения фирмы в следующих условиях. Все буквенные обозначения, введенные ранее, остаются в силе.
Альтернативная стоимость работы, определяемая рыночной ставкой заработной платы, такова, что её полезность равна 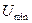 равна u.
равна u.
Функция полезности для работника имеет следующий вид:
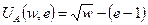 | (2) |
Целевой функцией для фирмы является величина чистого дохода, т.е. величина дохода минус величина вознаграждения работника 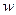 .
.
Уровень усилий работника может принимать два значения, 1 и 2.
| Усилия работника | е= | |||
| Период | неудачный | удачный | ||
| Доход фирмы | R | 20-d | 40+d | |
| Вероятность | P | 2/3+a | 1/3-a |
Рис. 19. Возможный доход фирмы в зависимости от состояния рынка (удачности или неудачности периода) при низком уровне усилий работника
| Усилия работника | е= | |||
| Период | неудачный | удачный | ||
| Доход фирмы | R | 20-b | 40+b | |
| Вероятность | P | 1/3-c | 2/3+c |
Рис. 20. Возможный доход фирмы в зависимости от состояния рынка (удачности или неудачности периода) при высоком уровне усилий работника.
Значения параметров a, b, c, d и u задаются преподавателем в зависимости от варианта.
- Найти ожидаемые значения заработной платы и полезности работника, дохода и прибыли фирмы в условиях симметричности информации. Провести имитационное моделирование таких контрактов. Сравнить полученные результаты.
- Определить оптимальные значения стимулирующих выплат в условиях несимметричности информации. Решение провести двумя (кто может тремя) способами: 1) графически; 2)с помощью надстройки «Поиск решения»; 3) решив аналитически (?!) или приближенно задачу квадратичного программирования.
- Сравнить полученные результаты.
- Провести имитационное моделирование контракта при оптимальных значениях стимулирующих выплат
- Провести имитационное моделирование контракта при отсутствии стимулирующих выплат.
- Сравнить полученные результаты. Сделать вывод о целесообразности заключения контракта того или иного вида.
РЕКОМЕНДАТЕЛЬНЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Курицкий Б.Я. Поиск оптимальных решений средствами EXCEL 7.0.- СПб.: BHV- СПб. 1997.
- Юдкевич М. М., Подколзина Е. А., Рябинина А. Ю. Основы теории контрактов: модели и задачи: учеб. пособие. М.: ГУ ВШЭ, 2002.
- Тамбовцев В. Л. Введение в зкономисческц\ую теорию контрактов: учеб. пособие. М.: ИНФРА-М, 2004. -144с.
Приложение1
