История и свойства последовательности
Леопард Фибоначчи (XII ~ XIIIв. н.э., Италия, Пиза) — один из
величайших математиков Средневековья. Именно ему мы обязаны
использованием десятичной системы исчисления. В одном из сво-
их трудов "Книга вычислений" Фибоначчи описал индо-арабскую
систему исчисления и преимущества ее использования перед римс-
кой. Мы имеем возможность пользоваться этими преимуществами
и по сей день.
И однако же — почему имя великого Фибоначчи неразрывно
связано с техническим анализом рынков?
Причина заключается в так называемой числовой последова- телыности Фибоначчи, состоящей из цифр 1,1,2,3,5,8,13,21,34, 55, 89,144... Фибоначчи открыл се при наблюдении роста потомства у семьи кроликов. Задача была поставлена следующим образом: "Сколько кроликов, помещенных в клетку, можно получить в год от одной пары, если каждая пара производит новую каждый месяц, начиная со второго?" Каждое из чисел последовательности Фибоначчи представляет собой количество пар кроликов в каждый месяц соответственно своему порядковому номеру.
Числовая последовательность Фибоначчи имеет много интересных свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.). Интересующиеся темой особых свойств чисел в последовательности Фибоначчи могут найти ее освещение как в соответствующих математических трудах, так и в некоторых книгах по техническому анализу.
Одним из самых главных следствий этих свойств является существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений различных членов последовательности. Они определяются следующим образом:
1. Отношение каждого числа к последующему более и более
стремится к 0.618 по увеличении порядкового номера (см. табли-
цу). Отношение же каждого числа к предыдущему стремится к
1.618 (обратному к 0.618). Число 0.618 называют ф (фи), и мы
поговорим о нем подробнее немного позже.
· При делении каждого числа на следующее за ним через од-
но, получаем число 0.382; наоборот — соответственно 2.618.
2. Подбирая таким образом соотношения, получаем основной
набор фибоначчиевских коэффициентов:... 4.235,2.618,1.618,0.618,
0.382, 0.236 (рис. 5.1). Упомянем также 0.5 (1/2). Все они играют
особую роль в природе, и в частности — в техническом анализе.
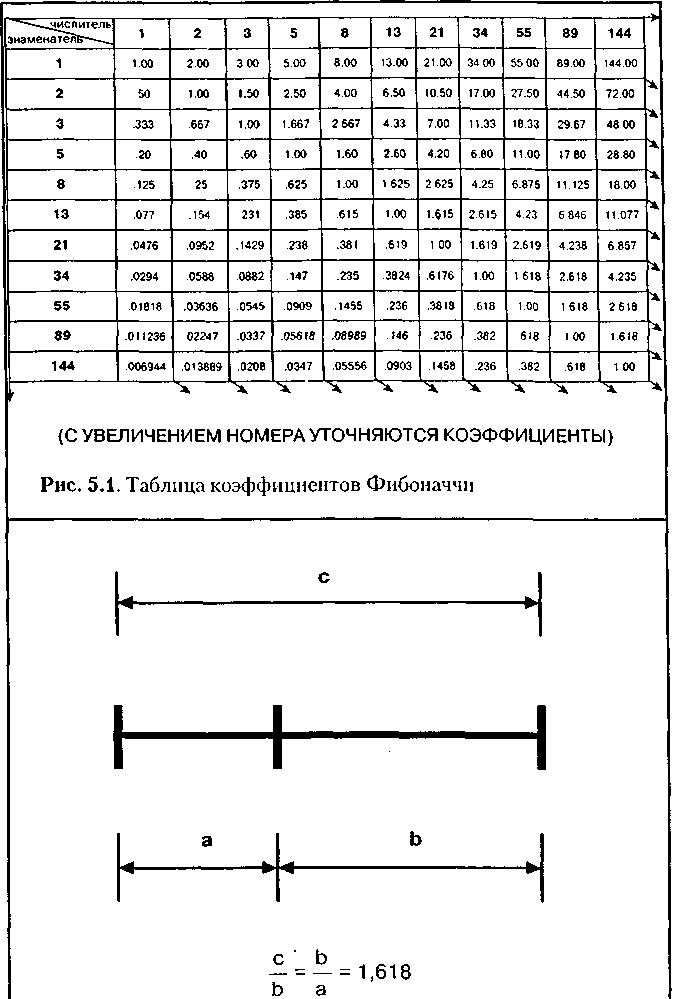 |
Рис. 5.2. Золотое сечение
Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам, которые использовали коэффициент Ф при строительстве Парфенона и пирамид. Более того, они рассматривали Ф не только как число, но и как символ созидательных функций. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи.
Например, число 0.618 представляет собой постоянный коэффициент в так называемом золотом сечении (рис. 5.2), где любой отрезок делится таким образом, что соотношение между его меньшей и большей частью равно соотношению между большей частью и всем отрезком. Таким образом, число 0.618 (или 1.618) известно еще как золотой коэффициент или золотая середина. Такого типа пропорцию можно встретить абсолютно везде — и в структуре ДНК, и в произведениях великих художников (рис. 5.3).
Золотой коэффициент используется природой для построения ее частей, начиная от больших и заканчивая малыми. Современная наука считает, что Вселенная развивается по так называемой золотой спирали (рис. 5.4 а), которая строится именно с помощью золотого коэффициента. Эта спираль в буквальном смысле не имеет конца и начала. Как более крупные, так и менее крупные ее витки имеют одну и ту же форму. Меньшие витки никогда не сходятся в одну точку, а большие неограниченно развиваются в пространстве. Так описываются траектории движения комет и метеоритов, рост количества бактерий, форма ананаса и раковины моллюсков, и даже строение человеческого уха (рис. 5.4 б).
Сами по себе свойства числовой последовательности и коэффициентов Фибоначчи представляют собой отдельную и очень интересную тему. Самое важное заключается в том, что с помощью всех этих, в каком-то роде мистических, чисел, описываются разнородные процессы во Вселенной. Опустимся на землю и выскажем смелую мысль — почему бы не использовать Последовательность Фибоначчи при прогнозировании цены, т.е. в техническом анализе?
Эта мысль действительно смелая. Ее высказал еще в 30-е годы один из самых известных людей, внесших вклад в теорию технического анализа, — Ральф Нельсон Эллиотт. С тех пор конкретная польза применения этой идеи практически во всех методах технического анализа не вызывает сомнения. Как мы увидим, в некоторых методах числа Фибоначчи применяются в неявном виде. Это, конечно, является одним из лучших подтверждений их роли в устройстве мира.
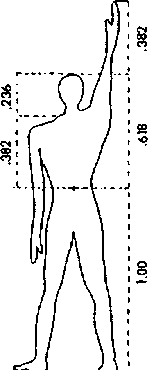
ПРОПОРЦИИ ЧЕЛОВЕКА
МОЛЕКУЛ А ДНК
 |
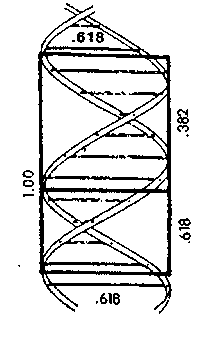 |
Рис. 5.3. Коэффициенты Фибоначчи в строении человека и ДНК Из кн.: A. Frost, R. Prechter "Elliott Wave Principle"
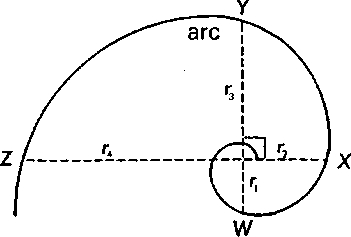
Рис. 5.4 а. Золотая спираль
Некоторые из соблюдающихся соотношений:
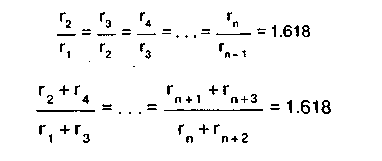
Из кн.: A. Frost, R. Prcchter: "Elliott Wave Principle"
 |
Росток
 |
 |
 |
Рога
Водоворот
Морской конек
Ананас
Ракушки
Рис. 5.4 б. Золотая Спираль в природе
Из кн.: A. Frost, R. Prechter "Elliott Wave Principle"
