Добавление и удаление элемента

Билет.

Теория

Динамические структуры данных – это структуры данных, память под которые выделяется и освобождается по мере необходимости.Для решения проблемы адресации динамических структур данных используется метод, называемый динамическим распределением памяти, то есть память под отдельные элементы выделяется в момент, когда они "начинают существовать" в процессе выполнения программы, а не во время компиляции. Компилятор в этом случае выделяет фиксированный объем памяти для хранения адреса динамически размещаемого элемента, а не самого элемента.

Динамическая структура данных характеризуется тем, что:

• она не имеет имени;
• ей выделяется память в процессе выполнения программы;
• количество элементов структуры может не фиксироваться;
• размерность структуры может меняться в процессе выполнения программы;
• в процессе выполнения программы может меняться характер взаимосвязи между элементами структуры.

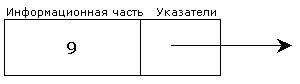
Динамические структуры строятся из динамических элементов. Динамический элемент состоит из двух частей:

· информационная часть

· указатели

Пример описания и работы с динамической структурой ( список):

struct tsMyStruct

{

double Data1;

int Data2;

char String[80];

tsMyStruct *Next;

};

void main()

{

tsMyStruct *Head, *Temp;

Head= new tsMyStruct;

Head->Next= new tsMyStruct;

Temp=Head->Next;

Temp->Next= new tsMyStruct;

Temp->Next->Next= new tsMyStruct;

Temp->Next->Next->Next=NULL;

delete Temp->Next->Next;

delete Temp->Next;

delete Head;

delete Temp;

}

Виды списков : Однонаправленные, двунаправленные, циклические

Однонаправленные (объявление)

struct tsMyStruct

{

double Data1;

int Data2;

char String[80];

tsMyStruct *Next;

};

Двунаправленные (объявление)

struct tsMyStruct

{

double Data1;

int Data2;

char String[80];

tsMyStruct *Next;

tsMyStruct *Previous;

};

Циклические

При объявлении циклического списка, следующий элемент после последнего указывает на первый (объявление будет характерно для конкретного примера)

Добавление и удаление элемента

1)Добавление звена в начало списка

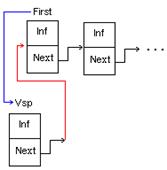
Zveno *V_Nachalo(Zveno *First, BT X)

{ Zveno *Vsp;

Vsp = (Zveno *) malloc(sizeof(Zveno));

Vsp->Inf=X;

Vsp->Next=First;

First=Vsp;

return First;

}

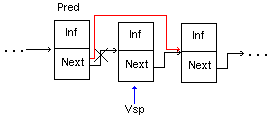
2)Добавление звена в произвольное место списка, отличное от начала

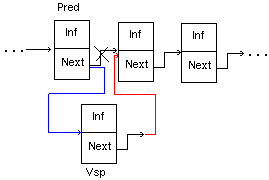Zveno *V_Spisok(Zveno *Pred, BT X){ Zveno *Vsp; Vsp = (Zveno *) malloc(sizeof(Zveno)); Vsp->Inf=X; Vsp->Next=Pred->Next; Pred->Next=Vsp; return Vsp;}

3)Удаление звена из начала списка

Zveno *Iz_Nachala(Zveno *First){ Zveno *Vsp; Vsp=First->Next; free(First); return Vsp;}

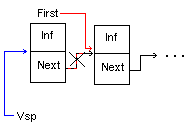
4)Удаление звена из произвольного места списка, отличного от начала

BT Iz_Spiska(Zveno *Pred){ BT X; Zveno *Vsp; Vsp=Pred->Next; Pred->Next=Pred->Next->Next; X=Vsp->Inf; free(Vsp); return X;}

Билет.

Теория

Дерево – это структура данных, представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов .Каждый элемент дерева называется вершиной (узлом) дерева. Вершины дерева соединены направленными дугами, которые называют ветвями дерева. Начальный узел дерева называют корнем дерева, ему соответствует нулевой уровень. Листьями дерева называют вершины, в которые входит одна ветвь и не выходит ни одной ветви.

Остальная теория та же, что и в 11 билете

Объявление дерева( бинарное)

struct tsMyStruct

{

double Data1;

int Data2;

char String[80];

tsMyStruct *Left;

tsMyStruct *Right;

};

Классификация деревьев

По числу возможных потомков у вершин различают двоичные (бинарные) или недвоичные (сильноветвящиеся) деревья.

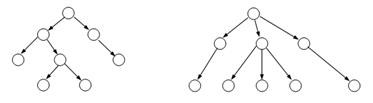
Если в дереве важен порядок следования потомков, то такие деревья называют упорядоченными.Для них вводится понятие левый и правый потомок (для двоичных деревьев) или более левый/правый (для недвоичных деревьев). В этом смысле два следующих простейших упорядоченных дерева с одинаковыми элементами считаются разными:

Классификация бинарных деревьев

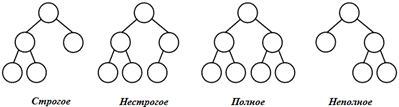
• строгие – вершины дерева имеют степень ноль (у листьев) или два (у узлов);
• нестрогие – вершины дерева имеют степень ноль (у листьев), один или два (у узлов).

В общем случае у бинарного дерева на k -м уровне может быть до 2^k-1 вершин. Бинарное дерево называется полным, если оно содержит только полностью заполненные уровни. В противном случае оно является неполным.

Дерево называется сбалансированным, если длины всех путей от корня к внешним вершинам равны между собой. Дерево называется почти сбалансированным, если длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.

Двоичные деревья

Двоичные деревья (ДД) используются наиболее часто и поэтому представляют наибольший практический интерес. Каждая вершина ДД должна иметь два связующих поля для адресации двух своих возможных потомков.

ДД можно реализовать двумя способами:

• на основе массива записей с использованием индексных указателей
• на базе механизма динамического распределения памяти с сохранением в каждой вершине адресов ее потомков (если они есть)

Второй способ является значительно более удобным и поэтому используется наиболее часто. В этом случае каждая вершина описывается как запись, содержащая как минимум три поля: информационную составляющую и два ссылочных поля для адресации потомков:

struct TREE {
int Info;
TREE *Right;
TREE *Left;
};