Двойственный симплекс-метод

Двойственный simplex-метод можно применять при решении ЗЛП, свободные члены системы огран-ий кот-ых могут быть любыми числами. Постановка задачи: F=c₁x₁+c₂x₂+…+c_nx_n→max (1) x₁p₁+x₂p₂+…+x_np_n=p₀ (2) x_i≥0, i=1,n (3). p₀ состоит из чисел b_i, среди кот есть отр-ые. Опр. Решение x=(b₁,b₂,…, b_m,0,…,0)(4) системы лин ур-ий(2) определяемое базисом p₁,p₂,…,p_m наз-ся псевдопланом задачи (1)-(3), если Δj≥0 , j=1,n.

Теорема1: если в псевдоплане (4), опр-ом базисом p₁,p₂,…,p_m есть хотя бы 1-о отр-ое число b_i, такое что все a_ij≥0, то задача (1)-(3) вообще не имеет плана.

Теорема2: если в псевдоплане (4), опр-ом базисом p₁,p₂,…,p_m имеются отр-ые числа b_i, такие что для любого из них имеются числа a_ij<0, то можно перейти к новому псевдоплану при котором значение целевой ф-ии задачи (1)-(3) не уменьшается.

Алгоритм двойственного simplex-метода:

1) Находят псевдоплан задачи;

2) Проверяют его на оптим-ть: если псевдоплан оптим-ен, то найдено реш задачи, иначе уст-ют либо неразрешимость задачи, либо переходят к новому псевдоплану;

3) Выбирают разрешающую строку с помощью опр-ия наиб-его по абс величине отр-ого числа столбца-вектора р₀ и разрешающий столбец, с помощью нахождения наим-его по абс величине отношения элементов индексной строки к соотв-им отр-ым эл-ам разрешающей строки;

4) находят новый псевдоплан и проверяют его на оптим-ть.

8. Постановка транспортной задачи. Суть метода потенциалов.

Постановка: Имеется m пунктов отправления A₁,…,A_m с запасами грузов в них a₁,…,a_m и n пунктов назначения B₁,…,B_n с потребителями b₁,…,b_n. Известны стоимости перевозки единицы груза от i-го пункта отправления к j-му пункту назначения. Требуется развести весь груз и удовлетворить все заявки пунктов назначения так, чтобы при этом суммарная стоимость перевозки грузов была min. Составим мат модель: Пусть x_ij – кол-во единиц груза, перевозимого из i-ого пункта отправления в j-ый пункт назначения. Условия ограничения по запасам и заявкам:

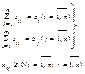
Целевая ф-ия: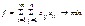

Если вып-ся условие: 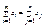, то задача наз-ся закрытой, в противном случае транспортная задача будет открытой.

Методы нахождения исходного опорного плана:

1) метод северо-западного угла;

2) метод min стоимости;

3) метод двойного предпочтения.

Стратегия решения трансп-ой задачи:

1. проверяем модель задачи на закрытость (если открытая, то закрываем)

2. нахождение исходного опорного плана

3. проверка плана на оптимальность (если оптим-ен, то решение закончено)

4. переходим к новому опорному плану и проверяем его на оптимальность

Пункты 3 и 4 основаны на теореме:

Теорема: Опорный план трансп-ой задачи оптимален Û, когда выполняются условия: u_i+v_j=c_ij для x_ij>0 (для занятых клеток) и u_i+v_j£c_ij для x_ij=0 (для свободных клеток) (i=1,…,m; j=1,…,n). Числа u_i, v_j, называются потенциалами соответственно i-го поставщика и j-го потребителя.

Каждому поставщику (ограничению по запасам) поставим в соответствие потенциал u_i, (i=1,…,m), а каждому потребителю (ограничению по спросу) – потенциал v_j (j=1,…,n).

Алгоритм метода потенциалов:

1) построим опорный план по одному из правил;

2) вычислим потенциалы поставщиков и потребителей u_i и v_j (i=1,…,m; j=1,…,n), решив систему уравнений вида u_i+v_j=c_ij;

3) вычисляем оценки s_ij для всех свободных клеток по формуле s_ij=c_ij –(u_i+v_j). Если все s_ij³0, то полученный план явл-ся оптимальным. При этом, если все s_ij>0, то полученный оптимальный план единственный. В случае, если хотя бы одна оценка s_ij=0, имеем бесчисленное мн-во оптимальных планов с одним и тем же значением целевой ф-ции. Если же условие не выполняется, строим другой опорный план и возвращаемся к пункту 2.

9. Динамическое программирование. Вывод функционального уравнения Беллмана для задачи оптимального распределения ресурсов.

Постановка ЗДП: Пусть некоторая система находится в начальном состоянии S₀ и является управляемой. Благодаря некоторому управлению U она переходит из начального состояния в конечное. Управление U можно осуществить несколькими способами. Задача состоит в том, чтобы из множества управлений U найти такое оптимальное управление U*, при котором функция W(U*), характеризующая это управление, принимает экстремальное значение.

Для задач ЗДП характерна многошаговость решения задачи. Основным инструментом решения ЗДП. явл-ся принцип оптимальности Беллмана.

Задача об оптим-ом распр-ии ресурсов. Постановка задачи: Пусть n предприятий исп-ют некоторые ресурсы. Известно: если k-ому предприятию выделяется x_К единиц ресурсов, то от этих ресурсов предприятие получит f_k(х_К) продукции. Требуется распределить ресурсы в общем объёме А ед. между предприятиями так, чтобы суммарный выпуск продукции был максимальным.

Мат. модель задачи: j₁(х₁)+j₂(х₂)+…+j_n(х_n)®max – целевая ф-ия

Условия огр-ий: х₁+х₂+…+х_n=А, х_i³0 i=1,n

1) если ф-ии j_1,….,j_n - линейные функции, тогда это ЗЛП

2) если ф-ии j_1,….,j_n – нелинейные функции, то это ЗНП

3) если ф-ии j_1,….,j_n заданы таблично, то это ЗДП

Обозначим функцию Беллмана, как ¦_k(х) – это максимальное количество продукции, которое могут выпустить k предприятий, при этом a_k(х) – количество ресурсов, получаемых k-ым предприятием, при условии: оптимального распределения ресурсов между первыми k-1 предприятиями. Предположим, что ¦_k(х) известно. Необходимо вычислить ¦_k+1(х). Пусть k+1 предприятие получает t-единиц ресурсов, где 0<= t<= x. Тогда оно выпустит j_k+1(t) ед.продукции, при этом неиспользованных ресурсов остается в кол-ве (х-t) ед. В силу принципа оптимальности Беллмана необходимо распределить оставшиеся (х-t) ед.ресурсов между k предприятиями. Тогда общий выпуск продукции будет: j_к+1(t)+¦_k(x-t). Чтобы этот общий выпуск продукции был максимален необходимо величину t подобрать так, чтобы эта сумма достигала наибольшего значения т.е. ур-ие оптим-ого упр-ия Беллмана для данной задачи запишется: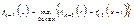

10. Элементы теории игр. Классификация игр. Матричные игры

Классификацию игр можно проводить:

1) В зав-ти от кол-ва игроков разл игры 2-х и n игроков;

2) По кол-ву стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она наз-ся конечной;

3) По хар-ру взаимодействия различ-ют бескоалиционные игры (игроки не имеют права образовывать коалиции) и коалиционные;

4) По виду ф-ий выйгрыша разл матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др игры.

Матричная игра – это конечная игра 2-х игроков с 0-ой суммой, в кот задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соотв номеру прим-ой стратегии игрока 1, столбец – номеру прим-ой стратегии игрока 2. На пересечении строки и столбца матр нах-ся выигрыш игрока. Для матричных игр доказано, что любая из них имеет реш-ие и оно может быть найдено путём сведения игры к ЗЛП. Биматричная игра – это конечная игра 2-х игроков с не 0-ой суммой, в кот выигрыши каждого игрока зад-ся матрицами отдельно для соотв игрока. Непрерывной считается игра, в кот ф-ия выигрышей каждого игрока явл-ся непрерывной в зав-ти от стратегий. Игра наз-ся выпуклой, если ф-ия выигрышей явл-ся выпуклой.

12. Решение матричных игр в чистых стратегиях.

Матричная игра 2-х игроков с 0-ой суммой может рассм-ся как след-ая абстрактная игра 2-х игроков: 1-ый игрок имеет m стратегий i=1,m; 2-ой имеет n стратегий j=1,n. Каждой паре стратегий (i,j)поставлено в соотв-ие число a_ij, выр-ее выигрыш игрока 1 за счёт игрока 2. Каждый игрок делает 1 ход: игрок 1 выбирает свою i-ую стратегию, игрок 2 – свою j-ую стратегию. После чего игрок 1 получает выйгрыш a_ij за счёт игрока 2 (если a_ij<0, то это означает, что игрок 1 платит 2-му сумму | a_ij|). На этом игра заканчивается. Каждая стратегия игрока часто наз-ся чистой стратегией. Рассм матрицу:

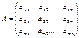проведение каждой партии матричной игры с матрицей А сводится к выбору игроком 1 i-ой строки, а игроком 2 j-ого столбца и получения игроком 1 выигрыша a_ij.

Стратегия игрока явл-ся оптим-ой, если применение этой стратегии обеспечивает ему гарант-ый , наиб-ий выигрыш при всевозможных стратегиях др игрока. Исходя из этих позиций исслед матрицу выигрышей А след образом:

Для каждого значения i=1, m опр-ся min значение выигрыша в зависимости от применяемых стратегий игрока 2 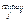, т.е. опр-ся min выигрыш для игрока 1 при условии, что он примет свою i-ую чистую стратегию, затем из этих min выйгрышей находится такая стратегия i=i₀, при которой этот min выйгрыш будет max, т.е.

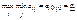. Число 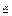-наз-ся чистой нижней ценой игры и показывает какой min выигрыш может гарант-ть себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. 2-ой игрок при опт-ом своём поведении должен стремится по возможности за счёт своих стратегий max уменьшить выигрыш 1-ого игрока, поэтому для игрока 2 находится 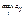, т.е. опр-ся max выигрыш 1-ого игрока при условии, что 2-ой игрок применит свою j-ую чистую стратегию, затем игрок 2 отыскивает такую свою j-ую стратегию j=j₁, при которой игрок 1 получит min выйгрыш, т.е. 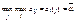. Число 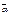- наз-ся чистой верхней ценой игры и пок-ет какой max выигрыш за счёт своих стратегий может себе гарант-ть 1-ый игрок. Др словами применяя свои чистые стратегии игрок 1 может обесп себе выигрыш не меньше 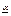, а игрок 2 за счёт применения своих чистых стратегий может не доп-ть выигрыш игрока 1 больше чем .

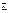Если в игре с матрицей А нижняя цена игры = верхней чистой цене игры ( 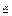= 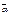), то говорят что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры ν= 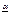= 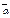. Седловая точка – это пара чистых стратегий (i₀,j₀) соотв игроков 1 и 2 при кот достигается рав-во 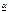= 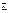: если один из игроков придерживается стратегии, соотв седловой точке, то др игрок не сможет поступить лучше чем придер-ся стратегии, соотв седловой точке. Отыскание Седловой точки: в матрице А послед-но в каждой строке находят min элемент, затем среди них отыскивают max – нижняя цена игры. В каждом столбце отыскивают max, а в строке min – верхняя цена игры. Пара чистых стратегий обр-ая седловую точку и седловой элемент ai_0j0 наз-ся решением игры. При этом i₀ j₀ наз-ся чистыми оптим-ми стратегиями соотв 1-ого и 2-ого игроков.

12. Смешанные решения матричных игр. Теорема о минимаксе. Свойства решений матричных игр.

Смешанной стратегией игрока наз-ся полный набор вероятностей применения его чистых стратегий. Т.о. если игрок 1 имеет m чистых стратегий, то его смешанная стратегия X- набор чисел Х=(Х1,Х2,…,Хm), удовл соотн Xi≥0 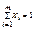. Аналогично для игрока 2, кот имеет n чистых стратегий смешанная стратегия У=(У1,У2,…,Уn), где У_j≥0 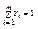. Т.к. каждый раз применения игроком 1 чистой стратегии искл применение др, то чистые стр-ии явл-ся несовместными событиями. Кроме того они явл-ся единств-ми возм-ми событиями. Чистая стратегия – есть частный случай смеш-ой стратегии. Средний выигрыш игрока 1 в матричной игре выр-ся в виде мат ожидания его выигрышей :Е(А,х,у)=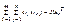

1-ый игрок имеет целью за счёт изм-ия своих смеш-ых стратегий Х max увел-ть свой средний выигрыш Е(А,х,у), а 2-ой за счёт своих смеш стр-ий стрем-ся сделать Е(А,х,у) min, т.е. для решения игры необходимо найти такие х и у, при которых достигается верхняя цена игры: 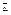= 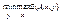. Аналогичной должна быть ситуация для 2-ого игрока, т.е. нижняя цена игры: = .

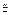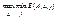Оптимальными смеш-ми стратегиями игроков 1 и 2 наз-ся такие наборы х⁰ и у⁰, соотв-но, которы удовл-ют рав-ву: 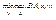= =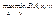E(A,x⁰,y⁰). Величина E(A,x⁰,y⁰) наз-ся ценой игры. Стратегии х⁰ и у⁰ наз-ся оптим-ми смеш-ми стр-ми соотв-но игроков 1 и 2 если они обр-ют седловую точку: Е(А,х,у⁰)≤ Е(А,х⁰,у⁰)≤ Е(А,х⁰,у). Оптим-ые смеш-ые стр-ии и цена игры Е(А,х⁰,у⁰) наз-ся решением матричной игры.

Теорема о минимаксе: для матр-ой игры с любой матрицей А величины 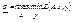и 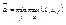сущ-ют и равны между собой.

Св-ва решений матричных игр.

Обозначим через G(x,y,A) игру двух лиц с нулевой суммой в которой первый игрок выбирает стратегию xЄX, а 2-ой игрок выбирает стратегию уЄY. После чего 1-ый игрок получает выигрыш А=А(x,y) за счёт игрока два.

Опр: 1.Стратегия x¹ 1-го игрока доминирует (строго доминирует) над стратегией x² , если выполняется : A(x¹,у) 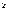A(x²,y) />), где у Є Y

2.Стратегия y¹ 2-го игрока доминирует (строго доминирует) над стратегией y² , если выполняется: A(x,y¹) 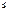A(x,y²) /<), где x Є X

При этом стратегии x² и y² называются доминирующими (строго доминирующими).

Опр: Спектром смешанной стратегии игрока в конечной антагонистичной игре называется множество всех его чистых стратегий вероятность которых согласно этой стратегии положительна.

Св-ва:

1) Если чистая стратегия одного из игроков содержится в спектре некоторой его оптимальной стратегии, то выигрыш этого игрока в ситуации образованной данной чистой стратегией и любой оптимальной стратегией другого игрока, равен значению конечной антагонистической игры.

2) Ни одна строго доминируемая чистая стратегия игрока не содержиться в спектре его оптимальных стартегий.

Опр: Игра G’=(x’,y’,A’) называется подигрой игры G(x,y,А), если x’ЄX, y’ЄY, матрица А’ является подматрицей матрицы А. При этом матрица А’ строиться следующим образом: в матрице А остаются строки и столбцы соответствующие стратегиям x’и y’, остальные вычеркиваються.

3) 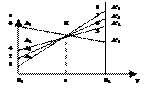Пусть G(x,y,А), конечная антагонистическая игра, G’=(X\x’,Y,A) подигра игры G, а x’ чистая стратегия игрока один в игре G, доминируемая некоторой стратегией 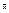, спектр которой не содержит x’. Тогда всякое решение (x⁰, y⁰, v) игры G’ является решением игры G.

4) Пусть G(x,y,А) конечная антагонистическая игра, G’=(X,Y\y’,A) подигра игры G, a y’ чистая стратегия игрока два в игре G, доминируемая некоторой стратегией 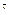, спектр которой не содержит y’. Тогда всякое решение игры G’ является решением игры G.

5) Если для чистой стратегии x’ игрока один выполняються условия св-ва 3, а для чистой стратегии у’ игрока два выполняются условия св-ва 4, то всякое решение игры G’=(X\x’,Y\y’,A) являются решением игры G(x,y,А).

6) (x⁰, y⁰, v) являются решением игры G(x,y,А) тогда и только тогда, когда (x⁰, y⁰, kv+a) является решением игры G(x,y,кА+а), где a – любое вещественное число и k>0.

13. Сведение матричной игры к задаче линейеного программирования.

Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.

Итак, пусть дана матричная игра с матрицей А порядка m х n. Согласно свойству 7 оптимальные смешанные стратегии х = (х₁, ..., х_m), y = (y₁, ..., y_n) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.

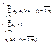
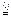
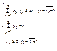
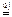
Разделим все уравнения и неравенства в (1) и (2) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения :

, ,

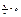
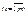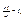
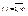Тогда (1) и (2) перепишется в виде :

, , , ,

, , , .

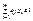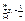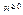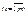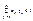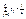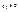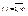Поскольку первый игрок стремится найти такие значения х_i и, следовательно, p_i , чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений p_i (i=1..m), при которых

, .

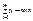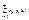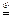
Поскольку второй игрок стремится найти такие значения y_j и, следовательно, q_j, чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений q_j, 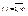, при которых

, .

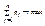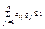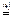
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).

Решив эти задачи, получим значения p_i , q_j и u.Тогда смешанные стратегии, т.е. x_i и y_j получаются по формулам :

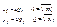
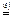
14. Экономическая интерпретация итоговой симплекс-таблицы.

Некоторая фирма производит три вида продуктов X, Y, Z в условиях ограничений на три вида сырья: N1, N2 и N3. Целью фирмы является выбор такого ассортиментного набора, при котором достигается максимум прибыли в неделю. В каждое ограничения модели вводятся остаточные переменные Si.

В процессе решения мы получили данную итоговую симплекс-таблицу.

Базисные переменные	B	A1	A2	A3	S1	S2	S3
Z			0,125		0,375		-0,25
S2			2,125		-1,625		0,75
X			1,25		-0,25		0,5
M+1			37,5		2,5

Значения базисных переменных находятся в соответствующих строках столбца B. Следовательно, X= 200 ед. в неделю; Z = 95 ед. в неделю, а значение остаточной переменной для сырья 2 составило 175 ед. в неделю. Остаточные переменные s1 и s3 равны нулю. Это означает, что данные ограничения являются лимитирующими, а сырье типов 1 и 3 расходуется полностью. Также нулю равно значение Y, следовательно, для достижения максимума прибыли продукт Y производить не требуется. Оптимальное значение целевой функции указано в строке целевой функции столбца B и равно 21700.

Теневая цена для ограничения 1, т.е. цена ресурса N1, составляет 2,5 д.ед., а теневая цена для ограничения 3 - 25 д.ед. Это означает, что если реализуется 1 ед. ресурса N1 сверх нормативного запаса, прибыль за неделю возрастает на 2.5 д.ед.

Оставшиеся крайние значения итоговой таблицы — это элементы, лежащие на пересечении строки "целевая функция" и столбцов переменных задачи. Оптимальный ассортиментный набор для этого решения — это выпуск только продуктов X и Z в количестве 200 и 95 единиц. Если по тем или иным причинам некоторое количество продукта Y все же необходимо произвести, значение целевой функции уменьшится на 37,5 д.ед., приходящихся на каждую производимую единицу продукта Y.

15. Экономическая интерпретация графического метода решения экономической задачи линейного программирования.

Любая экономико-математическая модель лишь упрощенно грубо отображает реальный экономический процесс, и это упрощение существенно сказывается на получаемых результатах. Из симплекс-таблицы можно получить информацию относительно:

· оптимального решения;

· статуса ресурсов;

· ценности каждого ресурса;

· чувствительности оптимального решения к изменению запасов ресурсов, вариациям коэффициентов целевой функции и интенсивности потребления ресурсов.

Сведения, относящиеся к первым трем пунктам, можно извлечь непосредственно из итоговой симплекс-таблицы и с помощью графической интерпретации. Получение информации, относящейся к четвертому пункту, требует дополнительных вычислений.

Рассмотрим задачу: определение оптимального ассортимента продукции.

Предприятие изготавливает два вида продукции – П₁ и П₂, которая поступает в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции вида П₁ и П₂ дан в таблице.

Расход сырья продукции

Сырье	Расход сырья на 1 единицу продукции	Запас сырья, ед.
П1	П2
А В

Опыт показал, что суточный спрос на продукцию П₁ никогда не превышает спроса на продукцию П₂ более чем на 1 ед. Кроме того, известно, что спрос на продукцию П₂ никогда не превышает 2 ед. в сутки.

Оптовые цены единицы продукции равны: 3 д.е. – для П₁ и 4 д.е. для П₂.

Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?

Получим оптимальное решение нашей задачи с помощью графического метода.

Построим многоугольник решений. Для этого в системе координат Х₁ОХ₂ на плоскости изобразим граничные прямые:

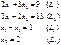
Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, будем обозначать стрелками.

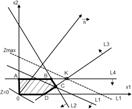
Областью решений является многоугольник OABCD.

Для построения прямой Z=3x₁+4x₂=0 (целевая функция) строим вектор-градиент 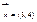и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора С. Из рис. следует, что по отношению к многоугольнику решений опорной, эта прямая становится в точке С, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L₁ и L₃. Для определения ее координат решим систему уравнений:

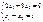
Оптимальный план задачи х₁=2,4; х₂=1,4. Подставляя значения х₁ и х₂ в линейную функцию, получим: Z_max=12,8.

Произведем экономическую интерпретацию полученного решения с помощью графического метода. Для этого рассмотрим основные задачи анализа на чувствительность.

После нахождения оптимального решения выясним, как отразится на оптимальном решении изменение запасов ресурсов. Для этого необходимо рассмотреть два вопроса:

1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции Z?

2. На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?

Прямая, представляющая связывающее ограничение, должна проходить через оптимальную точку, в противном случае, соответствующее ограничение будет несвязывающим. На нашем графике связывающими ограничениями являются ограничения (1) и (3), представленные прямыми L₁ и L₃ соответственно, т.е. те, которые определяют запасы исходных ресурсов. Ограничение (1) определяет запасы сырья А. Ограничение (3) определяет соотношение спроса на выпускаемую продукцию.

Если некоторое ограничение является связывающим, то соответствующий ресурс относят к разряду дефицитных ресурсов, т.к. он используется полностью. Ресурс, с которым ассоциировано несвязывающее ограничение, следует отнести к разряду недефицитных ресурсов (т.е. имеющихся в некотором избытке). В нашем примере несвязывающими ограничениями являются ограничения (2) и (4). Следовательно, ресурс – сырье В – недефицитный, т.е. имеется в избытке, а спрос на продукцию П₂ не будет удовлетворен полностью, а сырье А и соотношение спроса на выпускаемую продукцию П₁ и П₂ являются дефицитными ресурсами.

При увеличении запаса этого ресурса прямая L₁ перемещается вверх, параллельно самой себе, до точки К, в которой пересекаются линии ограничений L₂, L₃ и L₄. В точке К ограничения (2), (3) и (4) становятся связывающими; оптимальному решению при этом соответствует точка К, а пространством (допустимых) решений становится многоугольник АКD0. В точке К ограничение (1) (для ресурса А) становится избыточным, т.к. любой дальнейший рост запаса соответствующего ресурса не влияет ни на пространство решений, ни на оптимальное решение.

Таким образом, объем ресурса А не следует увеличивать сверх того предела, когда соответствующее ему ограничение (1) становится избыточным, т.е. прямая (1) проходит через новую оптимальную точку К.

16. Первая нормальная форма.

Дать определение 1НФ сложно ввиду его тривиальности. Поэтому имеет несколько объяснений.

Объяснение 1. Говорят, что отношение R находится в 1НФ, если определено на множестве доменов 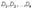(не обязательно различных), содержит две части: заголовок и тело (домены определены на простых типах данных).

Объяснение 2. Говорят, что отношение находится в 1НФ, если его атрибуты содержат только скалярные (атомарные) значения.

Объяснение 3. Отношение находится в 1НФ, если оно является плоской таблицей (ячейке таблицы не могут содержаться данные сложных типов: массивы, структуры, другие таблицы).

Итак выделим основные критерии первой нормальной формы:

•Все строки должны быть различными.

•Все элементы внутри ячеек должны быть атомарными (не списками). Другими словами, элемент является атомарным, если его нельзя разделить на части, которые могут использовать в таблице независимо друг от друга.

Непервую нормальную форму можно получить, если допустить, что атрибуты отношения могут быть определены на сложных типах данных - массивах, структурах, или даже на других отношениях. Легко себе представить таблицу, у которой в некоторых ячейках содержатся массивы, в других ячейках - определенные пользователями сложные структуры, а в третьих ячейках - целые реляционные таблицы, которые в свою очередь могут содержать такие же сложные объекты. Именно такие возможности предоставляются некоторыми современными пост-реляционными и объектными СУБД.

Пример не 1НФ таблицы:

Категория	Товары
Книги	Война и Мир, Азбука
Игрушки	Юла

В этом примере в одной из ячеек содержится список из двух элементов: Война и Мир, Азбука, т.е. он является не атомарным.

Исправить можно так:

Категория	Товары
Книги	Война и Мир
Книги	Азбука
Игрушки	Юла

Вот, теперь это таблица в первой нормальной форме.

Методы приведения к 1NF:

· Устранить повторяющиеся группы в отдельных таблицах (одинаковые строки).

· Создать отдельную таблицу для каждого набора связанных данных.

· Идентифицировать каждый набор связанных данных с помощью первичного ключа (добавить уникальный id для каждой строки)