Логическая модель представления знаний.(ПЗ)

Логическая модель ПЗ основана на использовании логики предикатов и имеет широкую область применения сопоставимую с продукционной моделью.

Основное преимущество: она обладает хорошо формализованным математическим аппаратом механизма логического вывода. Стратегию такого вывода удобно алгоритмизировать и реализовать в виде программы. Логической модели соответствует высокий уровень модульности знаний в которой отдельные элементы логически объединяются в единое целое, это позволяет определять знания в логической модели произвольным образом не заботясь в какой последовательности эти знания будут представлены и существует ли противоречие между новыми и существующими знаниями.

Недостатки: логики предикатов присущ чрезмерный уровень формализации знаний, т. к. трудно воспринимать формально представленные знания и невозможностью управления эффективностью логического вывода, что можно было сделать в продукционной модели.

Условно логическая модель описывается с помощью формул. Формула из одного предиката называется – атомарной.

Пример: Столица(Х,У) – логическая функция, где Х, У значения из множеств.

Х	У
Россия	Москва
Украина	Киев
Япония	Токио

Столица(Япония, Токио )=1 – представляет собой атомарную логическую формулу.

Столица(Россия, Васюки)=0

Помимо атомарных логические функции могут состоять из нескольких предикатов объединенных 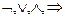, и имеющие связанные переменные при помощи квантора .

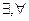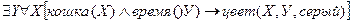
Для вычисления значений логических функций необходимо выполнить преобразования. Рассмотрим в более простой логической системе:

Система высказываний.

Предикат имеющий нулевой ранг, т. е. Количество аргументов функции равно 0, можно рассматривать как высказывание. Законы преобразующие логические формулы которые используются для выполнения операций над высказыванием, справедливы и для предикатных форм.

Пример:

А ”конь белый=1”

В ”конь черный=0”

Из атомарных высказываний можно написать составные. Для эквивалентных преобразований логических формул используются законы:

1) Переместительный закон: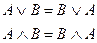

2) Распределительный закон: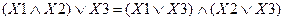

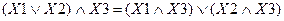
3) Сочетательный закон: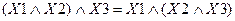

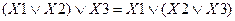
4) Закон инверсии. (Моргана)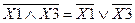

5) Закон двойного отрицания: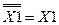

6) Закон исключения: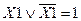

7) Закон противоречия: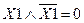

Эти законы можно использовать для выполнения действий над атомарными высказываниями и формулами любой сложности. Количество переменных, которое входит в состав сложных логических формул, называется рангом дизъюнкции \ конъюнкции , если все высказывания объединены отношением операций.

Дизъюнктивной нормальной формой называется логическая формула, состоящая из дизъюнкции атомарных высказываний, или их отрицаний.

ДНФ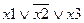

КНФ

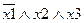
ДНФ – макстерм – функция, принимающая ложное значение для одного из возможных сочетаний.

КНФ – минтерм – функция, принимающая значение “правда” при одном из возможных сочетаний.

Совершенная ДНФ – дизъюнкция, состоящая из конъюнкций одинакового ранга.

СДНФ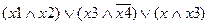

СКНФ 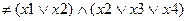- нарушен принцип одинакового ранга.

Лекция №7

Логика предикатов.

Суждения можно записать в виде:

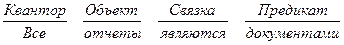
Разработка общей теории логических отношений, получила развитие благодаря исследованиям Г. Фреже, который выдвинул идею представить суждения в виде предикатной функции с некоторым количеством аргументов. P(x₁, . . . . ,x_n). Такая запись сходна с математическим обозначением функции и может быть использована для формализации доказательства ее истинности или ложности.

студент читает учебник

студентка книгу

журнал . . .

Смысл суждения зависит от глагола”читает” . Его и надо использовать для построения логической функции для обозначения предиката. Аргументами будут выступать значения переменных(x₁, - x₂), взятые из соответствующих множеств.

Читает (x₁, x₂)

Читает (грузчик, басни)

Истинность или ложность предиката будет зависеть от конкретного значения переменных. Они могут быть свободны, и тогда их подстановка из множества является произвольной, либо связанной кванторами. Фреже ввел основные определения общей теории логики предикатов.

Предикатом называют функцию, которая преобразует произвольное множество элементов в двух элементное множество, которое может принимать значение {0,1}, где 0- ложно, а 1- истинное значение предиката. P:Mⁿ 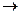E

E={0,1}

P(x₁, . . . . ,x_n), определенный на множестве М- это двухзначная функция от n аргументов.

Множество М- предметная область предиката. Аргументы (x₁, . . . . ,x_n)- предметные переменные, значения которых должны соответствовать определенной предметной области(ПО).Если для каждой переменной существует своя ПО,

P:M₁*M₂*. . . . Mn 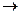E

Описания предикатов можно представить как функцию преобразования n- множеств в двух элементное множество М. Аргументами предиката могут являться константы, переменные, функции: P(a,x,f(a,x))

Общее наименование аргументов предиката- термы. Количество термов, определяющих значения логической функции, называют рангом предиката. Предикаты первого ранга называют - унарными , второго- бинарными, . . . Сравнивая высказывания и предикаты можно отменить, можно отметить основную отличительную особенность:

Если предикат является логической функцией, то высказывание является логической константой.

Предикаты- это выражения, содержащие некоторое множество переменных. Высказывания могут быть представлены как функции, не содержащие переменных. Высказывания можно отожествлять с предикатами, все переменные которых приняли определенные значения из множества.

Представим ПО, множеством которой являются наименования деревьев. Значение одноместного предиката при подстановке вместо х- одного из элементов множества, будет иметь истинное значение, если указать в качестве имени предиката обобщенное понятие, характерное для всех элементов, например “дерево”. Он будет истинен для любого значения из ПО.

М(береза, ель, сосна, . . .) P(x) Дерево (береза)=1

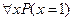
Если в качестве предиката выбрать лиственное дерево, то

Лиственное дерево(береза)=1

Лиственное дерево(ель)=0

Если в качестве предиката взять значение “березовая роща”, то предикат будет истинен и в том случае, если среди множества берез будет одна ель. Но предикат не будет истинным, если переменную х связать квантором всеобщности. Березовая роща(х)=0

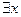Березовая роща(х)=1- будет истинным, пока в множестве М не будет одной березы.

Квантификация- мощное средство для формального описания суждений. Переменная является связанной, если на ней висит квантор, а остальные свободные. Область действия квантора в форме может быть указана при помощи скобок. Переменные, являющиеся аргументами кванторов, вынесенные за скобки, будут свободны.

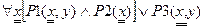, где

х- связанная для предиката 1 и 2 , а для 3- свободная. Большое значение имеет порядок следования кванторов в формулах.

Рассмотрим пример двухмерного предиката :

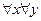Любит(x,y)

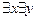Любит(x,y)

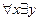Любит(x,y)

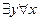Любит(x,y)

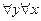Любит(x,y)- значение кванторов не имеет порядка, если кванторы разные, то имеет. Предикатные формулы называются эквивалентными, если при любых значениях переменных они принимают одинаковые логические значения. Существует несколько способов преобразования предикатных формул, которые не изменяют их эквивалентности.

1) 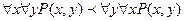, где 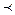- пропорциональность

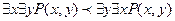
2)

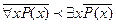
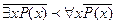
Квантор общности обладает свойством дистрибутивности.

3)

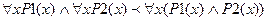
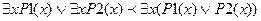
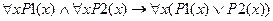
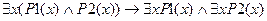
4)

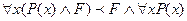
. . . . . . . . . . . . . . .путем подстановки значений переменных, взятых из множества М , описывающих ПО. Такой метод доказательства называется методом интерпретации. Им можно воспользоваться для доказательства эквивалентности формул лишь на конечных множествах n. При конечном множестве квантифицирующие предикаты могут быть представлены в виде конъюнктивной формулы для квантора общности.

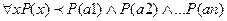
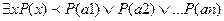
Используя эти отношения, любую сложную функцию логики предикатов можно преобразовать к формуле, состоящей из логических высказываний, соединенных знаками логических операций. Для бесконечного множества значений переменных метод интерпретации не подходит.

Тогда, необходимо использовать формальные процедуры, т. е. Правила вывода, которые порождали бы элементы, имеющие истинное или ложное значения, из исходных формул. Такие правила называются аксиомами, а теория- формальная. Использование формальных методов предполагает преобразование заданных формул в форму, удобную для реализации механизма формальной логики вывода. Необходимо привести сложную предикатную формулу в предиксно- нормальную форму (ПНФ), т. е. вынести за скобки все кванторы связанных переменных. Для получения такой формы можно использовать следующую процедуру:

1) Исключить из предикатной формулы операции импликации эквивалентности, оставив только ( 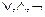). Для исключения импликации применяют преобразование:

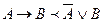
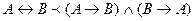
2) Использование операций вынесенных квантором за знак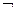

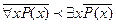
3) Осуществление свойства дистрибутивности .Может быть использована операция введения дополнительных переменных.

4) 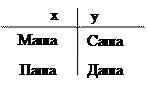Исключение кванторов существования. Для этого вводится дополнительная функция Сколема.

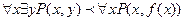
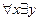Любит (х,у)

Любит (Паша, Даша)

Функция Сколема необходима, чтобы логическая формула в качестве своих аргументов имела бы переменные связанные только квантором общности. Принимая во внимание приоритетность действий кванторов слева на право, необходимо переменную связанную квантором существования, представить в виде функции переменных, связанных квантором общности и указанных в формуле слева от квантора существования.

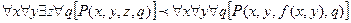
Лекция №8

Пример: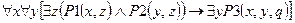

1)Преобразование начнем с того, что исключим импликацию.

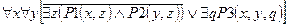
2) Вынесем квантор существования из под знака отрицания.

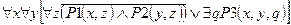
3)Применим правило Моргана, чтобы разделить.

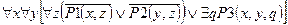
4)Приведем в логическую формулу и префиксно- нормальному виду.

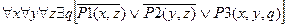
5) Применим функцию Сколема.

{q=(x,y,z)} x,y,z 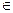M

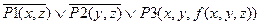
Рассмотрим некоторые дополнительные примеры функции Сколема.

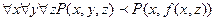
При составлении функции Сколема, необходимо включить только х, т. к. только х лежит слева от квантора существования.

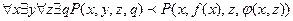
Переменная у заменяется функцией от х. а переменная q представляет собой функцию от х и z, т. к. именно эти переменные связаны квантором общности. Если переменная связанная квантором существования находится слева от квантора общности, переменная х м. б. Заменена константой.

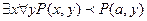
Множество логических формул после их преобразования образуют так называемое клаузальное множество . Это множество образовано из дизъюнктивно нормальной формы пример которой мы получили в результате преобразования. Если среди логических операций префиксно- нормальной формы содержатся операции конъюнкции, то необходимо произвести дополнительное преобразование сначала в КНФ затем разбить ее на отдельные предложения клаузального множества.

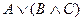
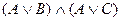
Тогда эту КНФ можно представить в виде отдельных предложений, которые содержат только операции дизъюнкции. Т.к. подобное преобразование справедливо и для предикатов можно записать пример:

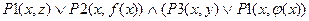
Это два клаузальных предложения, которые можно переписать так:

ДНФ

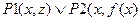и

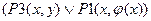
и рассмотреть и обработать отдельно.

Все предложения клаузального множества представляют собой совокупность предикатов и атомарных логических формул, связанных операцией дизъюнкции. Полученные предложения , входящие в клаузальные множества, потом рассматриваются как предложения Хорна. В этих предложениях принято различать позитивные и негативные литералы.

Позитивные- это предикаты и высказывания.

Негативные- это их отрицания.

Предложение Хорна- формировать позитивные и негативные литераль, размещая первые- в левой, вторые- в правой части. Это можно записать так:

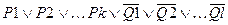
В зависимости от значений k и l, предложение Хорна относят к одному из следующих типов:

1. k=1, l=0 Состоит из одного позитивного литерала. Такими предложениями описываются факты, имеющие место в описывающей предметной области.

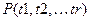- предикат, описывающий факт, включает в качестве аргументов множество термов - (переменных, констант, либо функций)

2. k=0, Предложение состоит из одного или нескольких негативных литералов, которые используются для формирования запросов в виде указания одной или нескольких целевых утверждений, требующих доказательства. Доказательство осуществляется альтернативным методом(опровержения). Этот метод предполагает описание отрицания некоторого утверждения, после чего доказывается, что это отрицание не выполнимо. Доказательством невыполнимости отрицания подтверждается истинность самого утверждения.

Например: требуется доказать, что человек совершил нечестный поступок. И если это не доказано, то человек честный.

Честный(х)

Честный(х)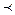

Предложение Хорна может содержать 1 или несколько негативных литералов, и требуется доказать их отрицание.

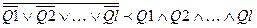
В результате, доказательства получаем истинность каждого из них.

3. k=1, Этот тип соответствует представлению суждения в виде импликации, т. к. выражение 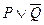может быть истолковано, как .

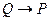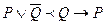
И если количество негативных литералов >1, то

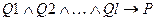
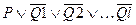
Часто, при описании той или иной ситуации, необходимо учитывать фактор времени, что позволяет описывать динамику изменения ситуации. Наиболее универсальным способом является введение в описание предикатов переменной, учитывающей момент времени.

P(x,t,V)

Значение предиката будет истинным только для определенного момента времени. Ограничиваясь лишь соотношением моментных состояний, можно получить различные утверждения для изменяющихся моментов времени, вводя в предложения клаузального множества логические формулы, описывающие такие утверждения, как “раньше, чем”, “позже”, ”одновременно”. (t1>t2)

Рассмотрим несколько примеров, характеризующих состояние времени.

1)

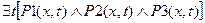
Когда я на почте служил ямщиком, . . .

Можно представить одновременность

“он был советник, - она- генеральская дочь”

2) 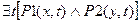Утверждение об изменении каких- то признаков. Можно представить с помощью различных значений аргументов времени.

3) “при испарении вода превращается в пар”

Жидкость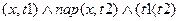

Или немного другая запись того же самого

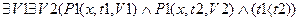Изменение времени характеризует изменение значения одного из предикатов.

Использование приведенных методик позволяет давать описание различного рода суждений о предметной области в виде совокупности логических формул, которые после преобразования объединяются в клаузальное множество и используются для формально- описания суждений.

1. “Оптическое стекло- это высоко прочное однородное, и химически- стойкое стекло”

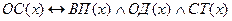
2. “Троллейбус- это безрельсовое транспортное средство”

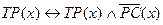
3. “Магнитный носитель- это магнитная лента или магнитный диск”

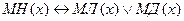
4. “Ротор- это вращающаяся часть машины”

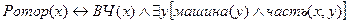
5. “Теплоход- это судно, приводимое в движение двигателем внутреннего сгорания”

6. Вакуумный насос- устройство для удаления газа и пара из сосудов.

Лекция №9