Свойства и основные тождества

Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:

;	;
;	;
;	;
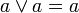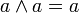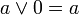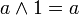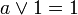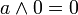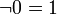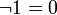;	;	дополнение 0 есть 1 и наоборот
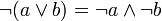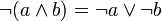;	;	законы де Моргана
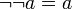.		инволютивность отрицания

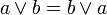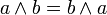;	.	1 коммутативность переместительность
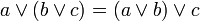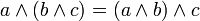;	.	2 ассоциативность сочетательность
3.1 конъюнкция относительно дизъюнкции	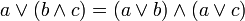3.2 дизъюнкция относительно конъюнкции	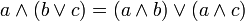3 дистрибутивность распределительность
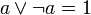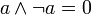;	.	4 комплементность дополнительность (свойства отрицаний)
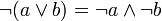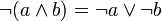;	.	5 законы де Моргана
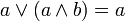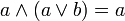;	.	6 законы поглощения
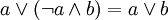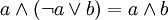;	.	7 Блейка-Порецкого
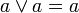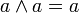;	.	8 Идемпотентность
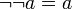.		9 инволютивность отрицания
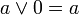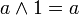;	.	10 свойства констант
;	.
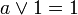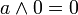дополнение 0 есть 1 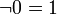;	дополнение 1 есть 0 .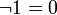
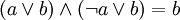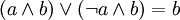;	.	11 Склеивание

Графы и деревья

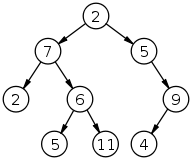Дерево (структура данных)

Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связанным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указываются, что рёбра графа не должны быть взвешенными.

Определения

· Корневой узел — самый верхний узел дерева.

· Корень — одна из вершин, по желанию наблюдателя.

· лист, листовой или терминальный узел — узел, не имеющий дочерних элементов.

· Внутренний узел — любой узел дерева, имеющий потомков, и таким образом не являющийся листовым узлом.

Дерево считается ориентированным, если в корень не заходит ни одно ребро.

В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин.

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Лекция №3. Конечные автоматы. Машина Тьюринга и машина Поста.

План лекций

1. Конечные автоматы.

2. Машина Тьюринга и машина Поста.

Ключевые слова:конечные автоматы, машина Тьюринга, машина Поста, управляющее устройство, детерминированный.

Иллюстративный материал:Таблица, схема.

Конечные автоматы

Конечный автомат-автомат, у которого множество состояний, а также множество входных и выходных сигналов являются конечными. Конечный автомат может быть моделью технического устройства (ЭВМ, релейное устройство) важными направлениями теории конечных автоматов (помимо традиционных задач и синтеза автоматических систем управления), имеющими большое практическое значение, являются синтез надежных элементов из ненадежных компонентов и исследование поведения конечных автоматов в случайных средах.

Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Существуют различные варианты задания конечного автомата. Например, конечный автомат может быть задан с помощью пяти параметров: 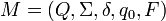, где:

• Q — конечное множество состояний автомата;
• q₀ — начальное (стартовое) состояние автомата ( );
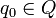• F — множество заключительных (или допускающих) состояний, таких что ;
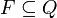• Σ — допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом;
• δ — заданное отображение множества 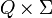во множество 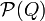подмножеств Q:

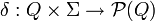
(иногда δ называют функцией переходов автомата).

Автомат начинает работу в состоянии q₀, считывая по одному символу входной строки. Считанный символ переводит автомат в новое состояние из Q в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допускающих состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается».

Конечные автоматы широко используются на практике, например в синтаксических, лексических анализаторах, и тестировании программного обеспечения на основе моделей.