Логическая модель представления знаний
В основе модели находится Булева логика, т.е. используются операции дизъюнкции и конъюнкции. Набор базовых эелемнтов:
L={T,P,A,F}
L – логическая модель;
T – множество терминальных (атомных )элементов, т.е. не подлежащих дальнейшему делению.
P – множество синтаксических правил, позволяющих стоить из множества Т элементов правильные выражения.
A – множество аксиом, т.е. априорно истинных выражений.
F – множество семантических правил, позволяющих расширить множество аксиом за счет новых выражений.
Пусть m –множество понятий и объектов предметной области. К- множество классов данного объекта, Мк – множество понятий разделенных на мно-во объектов опред-го К-класса.
Каждому классу ставиться в соответствие характеристическая функция представляя-я собой предикат. 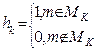
Проверяем на принадлежность. Вводится понятие предиката признака, которому ставиться в соответствие определенное св-во понятия или объекта.
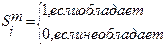
Каждому объекту m- ставится в соответствие его логическое описание, пред-т собой конъюнкцию всех предикатов признаков данного объекта.
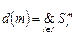
Для описания множ-ва объектов принадлежащих классу, вводится понятие Аксиомы класса Ак- дизъюнкция по j всех логических описаний:
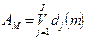
В идеальном случае при построении полного и непротиворечивого описания класса аксиома Aк д.б. равна характеристической функции (Aк=hk), таким образом формируется система понятий о предметной области на основе создания аксиом.
35. (Продолжение)
Для сокращения размерности аксиом в процессе обучения логической системы стоится оптимальное решающее правило: при построении коньюкции следующим выбирается предикат-признак, который максимизирует апостериорную вероятность того, что объект принадлежит данному классу.
Оптимальное решающее правило может быть представлено в виде бинарного дерева, в вершине которого находится признак с максимальной апостериорной вероятностью, а заканчивается дерево листьями, где указывает номер класса.
Сравнительная характеристика систем представления знаний на основе продукций и логической модели.
В логических системах для решения задач используется метод резолюций (доказательство от обратного), а в продукционных системах используется теория формальных грамматик Хомского.
Метод резолюций.
Метод резолюций – доказательства от обратного. Задача заключается виде логического условия или логической теоремы. Берется логическая формула и вычисляется др.логическая формула. Доказательство теоремы состоит в определении несовместимости и противоречия логической формулы и ее отрицание . Доказательство противоречивости свидетельствует о правильности логического вывода (Задача про робота с кубиками).
По принципу решения задачи необходимо построить отрицание с условием применимости, найти противоречие м\д условием применимости и его отрицании. Затем преминуть действие для преодоления противоречия.
Пошаговое выполнение задачи:
1).Строится цель перемещения, основная подцель, отрицание строим.
2).Выбираем любое из возможных действий. Если нет противоречия м\д отрицанием и условием применимости, то оператор сдвига применить нельзя. Чтобы было противоречие рассчитывается 3 шаг.
3).Сможем ли выполнить смещение оператора робота из точки d в точку а. Если есть противоречия, то можем применить оператор смещения.
4) Применение оператора смещения с использованием при этом список вычеркивания и добавления.d- это вычеркивание.
5) Возвращение к первому оператору- кандидату. Если существует противоречие, то для его устранения применяем оператор сдвига.
6) Применяем оператор сдвига…Дальше аналогично действия выполняются для второго объекта и .т.д.
