Решение произвольных систем линейных уравнений
Системы линейных уравнений.
Система вида
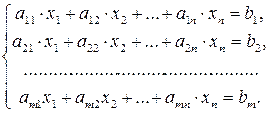 (1)
(1)
называется системой m линейных уравнений с n неизвестными.
Здесь 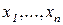 - неизвестные,
- неизвестные, 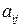 - коэффициенты при неизвестных,
- коэффициенты при неизвестных, 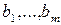 - свободные члены уравнений.
- свободные члены уравнений.
Если все свободные члены уравнений равны нулю, система называется однородной. Решением системы называется совокупность чисел 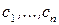 , при подстановке которых в систему вместо неизвестных все уравнения обращаются в тождества. Система называется совместной, если она имеет хотя бы одно решение. Совместная система, имеющая единственное решение, называется определенной. Две системы называются эквивалентными, если множества их решений совпадают.
, при подстановке которых в систему вместо неизвестных все уравнения обращаются в тождества. Система называется совместной, если она имеет хотя бы одно решение. Совместная система, имеющая единственное решение, называется определенной. Две системы называются эквивалентными, если множества их решений совпадают.
Система (1) может быть представлена в матричной форме с помощью уравнения
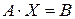 (2)
(2)
где
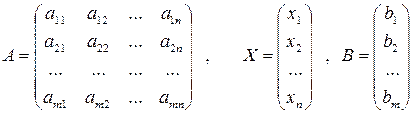 .
.
Совместность систем линейных уравнений.
Назовем расширенной матрицей системы (1) матрицу
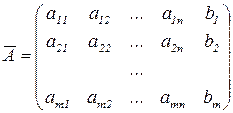
Теорема Кронекера - Капелли. Система (1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:
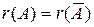 .
.
§3. Решение систем n линейных уравнений с n неизвестными.
Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:
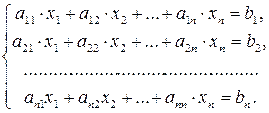 (3)
(3)
Теорема Крамера.Если главный определитель системы (3) 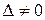 , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
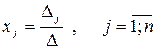
т.е. 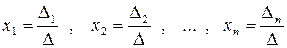 ,
,
где 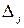 - определитель, получаемый из определителя
- определитель, получаемый из определителя 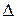 заменой
заменой 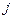 -го столбца на столбец свободных членов.
-го столбца на столбец свободных членов.
Если 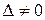 , а хотя бы один из
, а хотя бы один из 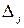 ≠0, то система решений не имеет.
≠0, то система решений не имеет.
Если 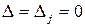 , то система имеет бесконечно много решений.
, то система имеет бесконечно много решений.
Систему (3) можно решить, используя ее матричную форму записи (2). Если ранг матрицы А равен n, т.е. 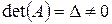 , то матрица А имеет обратную
, то матрица А имеет обратную 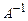 . Умножив матричное уравнение
. Умножив матричное уравнение 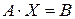 на матрицу
на матрицу 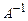 слева, получим:
слева, получим:
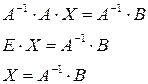 .
.
Последнее равенство выражает способ решения систем линейных уравнений с помощью обратной матрицы.
Пример.Решить систему уравнений с помощью обратной матрицы.
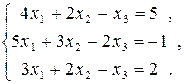
Решение.Матрица  невырожденная, так как
невырожденная, так как 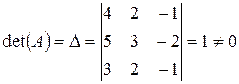 , значит, существует обратная матрица. Вычислим обратную матрицу:
, значит, существует обратная матрица. Вычислим обратную матрицу: 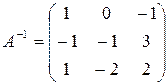 .
.
Тогда
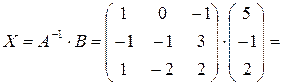
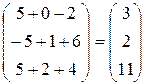 ,
,
т.е. 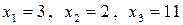 .
.
Задание. Решить систему методом Крамера.
Решение произвольных систем линейных уравнений.
Пусть дана неоднородная система линейных уравнений вида (1).
Предположим, что система совместна, т.е. выполнено условие теоремы Кронекера-Капелли: 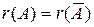 . Если ранг матрицы
. Если ранг матрицы 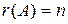 (числу неизвестных), то система имеет единственное решение. Если
(числу неизвестных), то система имеет единственное решение. Если 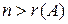 , то система имеет бесконечно много решений. Поясним.
, то система имеет бесконечно много решений. Поясним.
Пусть ранг матрицы r(A)=r<n. Поскольку 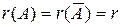 , то существует некоторый ненулевой минор порядка r. Назовем его базисным минором. Неизвестные, коэффициенты которых образуют базисный минор, назовем базисными переменными. Остальные неизвестные назовем свободными переменными. Переставим уравнения и перенумеруем переменные так, чтобы этот минор располагался в левом верхнем углу матрицы системы:
, то существует некоторый ненулевой минор порядка r. Назовем его базисным минором. Неизвестные, коэффициенты которых образуют базисный минор, назовем базисными переменными. Остальные неизвестные назовем свободными переменными. Переставим уравнения и перенумеруем переменные так, чтобы этот минор располагался в левом верхнем углу матрицы системы:
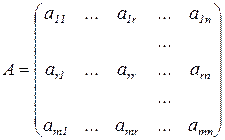 .
.
Первые r строк линейно независимы, остальные выражаются через них. Следовательно, эти строки (уравнения) можно отбросить. Получим:
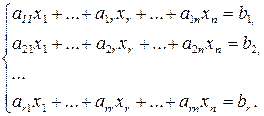
Дадим свободным переменным произвольные числовые значения: 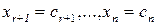 . Оставим в левой части только базисные переменные, свободные перенесем в правую часть.
. Оставим в левой части только базисные переменные, свободные перенесем в правую часть.
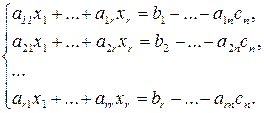
Получили систему r линейных уравнений с r неизвестными, определитель которой отличен от 0. Она имеет единственное решение.
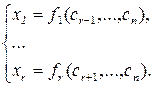
Эта система называется общим решением системы линейных уравнений (1). Иначе: выражение базисных переменных через свободные называется общим решением системы. Из него можно получить бесконечное множество частных решений, придавая свободным переменным произвольные значения. Частное решение, полученное из общего при нулевых значениях свободных переменных называется базисным решением. Число различных базисных решений не превосходит 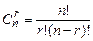 . Базисное решение с неотрицательными компонентами называется опорным решением системы.
. Базисное решение с неотрицательными компонентами называется опорным решением системы.
Пример. 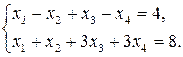
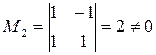 , r=2.
, r=2.
Переменные 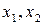 - базисные,
- базисные, 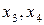 - свободные.
- свободные.
Сложим уравнения; выразим 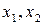 через
через 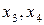 :
:
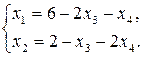 - общее решение.
- общее решение.
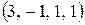 - частное решение при
- частное решение при 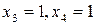 .
.
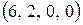 - базисное решение, опорное.
- базисное решение, опорное.
Метод Гаусса.
Метод Гаусса - это универсальный метод исследования и решения произвольных систем линейных уравнений. Он состоит в приведении системы к диагональному (или треугольному) виду путем последовательного исключения неизвестных с помощью элементарных преобразований, не нарушающих эквивалентности систем. Переменная считается исключенной, если она содержится только в одном уравнении системы с коэффициентом 1.
Элементарными преобразованиями системы являются:
- умножение уравнения на число, отличное от нуля;
- сложение уравнения, умноженного на любое число, с другим уравнением;
- перестановка уравнений;
- отбрасывание уравнения 0 = 0.
Элементарные преобразования можно совершать не над уравнениями, а над расширенными матрицами получающихся эквивалентных систем.
Пример.
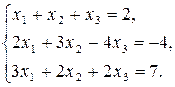
Решение. Выпишем расширенную матрицу системы:
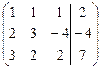 .
.
Выполняя элементарные преобразования, приведем левую часть матрицы к единичному виду: на главной диагонали будем создавать единицы, а вне ее - нули.
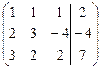
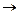
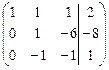
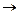
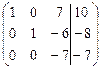
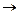
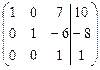
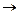
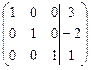
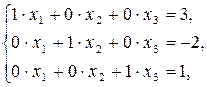
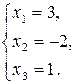
Замечание. Если при выполнении элементарных преобразований получено уравнение вида 0 = к (где к 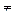 0),то система несовместна.
0),то система несовместна.
Решение систем линейных уравнений методом последовательного исключения неизвестных можно оформлять в виде таблицы.
Левый столбец таблицы содержит информацию об исключенных (базисных) переменных. Остальные столбцы содержат коэффициенты при неизвестных и свободные члены уравнений.
В исходную таблицу записывают расширенную матрицу системы. Далее приступают к выполнению преобразований Жордана:
1. Выбирают переменную 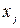 , которая станет базисной. Соответствующий столбец называют ключевым. Выбирают уравнение, в котором эта переменная останется, будучи исключенной из других уравнений. Соответствующую строку таблицы называют ключевой. Коэффициент
, которая станет базисной. Соответствующий столбец называют ключевым. Выбирают уравнение, в котором эта переменная останется, будучи исключенной из других уравнений. Соответствующую строку таблицы называют ключевой. Коэффициент 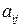 , стоящий на пересечении ключевой строки и ключевого столбца, называют ключевым.
, стоящий на пересечении ключевой строки и ключевого столбца, называют ключевым.
2. Элементы ключевой строки делят на ключевой элемент.
3. Ключевой столбец заполняют нулями.
4. Остальные элементы вычисляют по правилу прямоугольника. Составляют прямоугольник, в противоположных вершинах которого находятся ключевой элемент и пересчитываемый элемент; из произведения элементов, стоящих на диагонали прямоугольника с ключевым элементом, вычитают произведение элементов другой диагонали, полученную разность делят на ключевой элемент.
Пример.Найти общее решение и базисное решение системы уравнений:
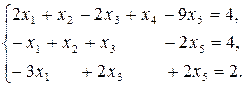
Решение.
| Базис | 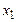 | 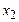 | 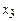 | 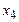 | 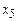 | 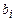 |
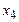 | -1 -3 |  1 1 | -2 | -9 -2 | ||
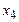 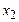 | -1 -3 | -3  2 2 | -7 -2 | |||
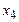 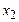 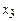 | -1,5 0,5 -1,5 | -4 -3 |
Общее решение системы :
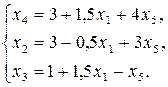
Базисное решение: 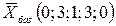 .
.
Перейти от одного базиса системы к другому позволяет преобразование однократного замещения: вместо одной из основных переменных в базис вводят одну из свободных переменных. Для этого в столбце свободной переменной выбирают ключевой элемент и выполняют преобразования по указанному выше алгоритму.
