Способ замены плоскостей проекций

Сущность способа состоит в том, что одну из заданных плоскостей проекций (П1 или П2) заменяют новой плоскостью П4 (рис. 52). При этом положение второй плоскости проекций и заданных геометрических фигур остается неизменным. Новая плоскость проекций П4 выбирается с таким расчетом, чтобы она занимала частное положение по отношению к рассматриваемой геометрической фигуре и была при этом перпендикулярной к незаменяемой плоскости проекций.

Таким образом, исходная (старая) система плоскостей проекций П2/П1 может быть преобразована в новую систему П2/ П4 при замене плоскости П1 плоскостью П4 П2 или в систему П4/П1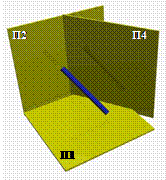
при замене плоскости П2 плоскостью П4П1 (рис.52).

Рис.52

Каждая из этих полученных систем может быть преобразована в новую путем замены плоскости проекций, не заменявшейся в предыдущем преобразовании. Таким образом, система П2/ П4 может быть преобразована в систему П5/П4 при замене плоскости П2 плоскостью П5 П4, а система П4/П1 - в систему П4/П5 - при замене плоскости П1 плоскостью П5П4 и т. д.

Такое последовательное преобразование исходной системы плоскостей проекций позволяет получить новую систему, в которой рассматриваемые геометрические фигуры окажутся в наивыгоднейшем положении относительно плоскостей проекций.

Большинство задач решается с применением одного или двух последовательных преобразований исходной системы плоскостей проекций. Одновременно можно заменять только одну плоскость проекций П1 (или П2), другая плоскость П2 (или П1) должна оставаться неизменной.

Все свойства геометрических фигур и их изображений, ранее рассмотренные в исходной П2/П1 системе, справедливы и для новой системы плоскостей проекций.

Каждая новая плоскость проекций П4, П5, ... условно называется так же, как та из основных, которую она заменяет.

Так, например, плоскость П4, заменяющая горизонтальную плоскость П1, условно называется также "горизонтальной", хотя она не занимает горизонтального положения в пространстве.

ПОЗИЦИОННЫЕ ЗАДАЧИ

Задачи, в которых определяется относительное положение или общие элементы геометрических фигур, называются позиционными.

К ним относятся задачи на принадлежность точки и линии поверхности, задачи, выражающие отношения между геометрическими фигурами, задачи на определение общих элементов геометрических фигур.

ПЕРВАЯ ПОЗИЦИОННАЯ ЗАДАЧА
(ПОСТРОЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ЛИНИИ И ПОВЕРХНОСТИ)

В зависимости от вида и взаимного расположения линии и поверхности точек их пересечения может быть одна или несколько. Например, прямая линия с алгебраической поверхностью n-го порядка пересекается в n точках. В основу их построения положен способ вспомогательных поверхностей, сущность которого состоит в том, что каждая из искомых точек рассматривается как результат пересечения двух линий, принадлежащих вспомогательной поверхности.

Одна из них является заданной линией, а вторая - линией пересечения вспомогательной и заданной поверхностей.
В соответствии с этим построение точек пересечения линии l и поверхности Ф (независимо от их вида) осуществляется по следующей общей схеме (рис. 54):

Рис. 54

1. Через данную линию l проводим вспомогательную
поверхность.

2. Определяем линию m пересечения вспомогательной и заданной Ф поверхностей.

3. Отмечаем точку А пересечения линий l и m, которая и является искомой.

В символической записи схема имеет вид:
1) проводим Θ כֿ l;
2) определяем m = Θ∩ Ф;
3) отмечаем А = l ∩ m = l ∩ Ф.

Поскольку линии l и m принадлежат одной и той же вспомогательной поверхности, они могут пересекаться, касаться и не иметь общих точек. В первом случае линия l пересекается с поверхностью Ф, во втором - касается ее, в третьем - не имеет с ней общих точек.

Для конкретной задачи на основании общей схемы составляется алгоритм ее решения. Алгоритмом называется совокупность однозначных последовательных операций, которые необходимо выполнить для решения данной задачи.

Схема преобразуется в алгоритм, если конкретизировать первый пункт, т. е. точно указать вид и положение вспомогательной поверхности, которая выбирается для определения точек пересечения заданных линии и поверхности.

Только после составления алгоритма можно перейти к решению (построению) задачи на комплексном чертеже.